2023年浙教版数学七年级上册4.6整式的加减同步测试（提升版）

试卷更新日期：2023-09-02 类型：同步测试

进入出卷网下载

一、选择题（每题2分，共20分）

1. 下列去括号正确的是（）

A、+(2x²-3x-1)=+2x²+3x+1 B、-0.5(1-2x)=-0.5+x C、1000(1- $\frac{x}{100}$ )=1000+x D、-(2x²-x+1)=-2x²+x

查看试题解析
2. 下列各式，去括号正确的是（　　）

A、 $x^{2} - (2 y - z) = x^{2} - 2 y - z$ B、 $a - [- (- b + c)] = a - b + c$ C、 $m - 2 (p - q) = m - 2 p + q$ D、 $a + (b - c - 2 d) = a + b - c + 2 d$

查看试题解析
3. 已知A＝a³-2ab²+1，B＝a³+ab²-3a²b，则A+B的值（）

A、2a³-3ab²-3a²b+1 B、2a³+ab²-3a²b+1 C、2a³+ab²+3a²b+1 D、2a³-ab²-3a²b+1

查看试题解析
4. 若整式 $- 100 a^{- m} b^{2} + 100 a^{3} b^{n} + 4$ 经过化简后结果等于4，则 $m^{n}$ 的值为（）

A、 $- 8$ B、8 C、 $- 9$ D、9

查看试题解析
5. 把两张形状大小完全相同的小长方形卡片（如图1）不重复地放在一个底面为长方形（长为8cm，宽为6cm）的盒子底部（如图2），盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是（）

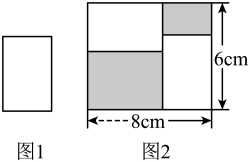A、28cm B、16cm C、32cm D、24cm

查看试题解析
6. 已知数a，b，c在数轴上的位置如图所示，化简|a+b|-|a-b|+|c-a|的结果为（）

A、-3a+c B、a-2b-c C、-a-2b+c D、-a+2b+c

查看试题解析
7. 有一道题目是一个多项式A减去多项式2x²+5x-3，小胡同学将2x²+5x-3抄成了2x²+5x+3，计算结果是-x²+3x-7，这道题目的正确结果是（）

A、x²+8x-4 B、-x²+3x-1 C、-3x²-x-7 D、x²+3x-7

查看试题解析
8. 今天数学课上学习了整式的加减，放学后，小明回到家，拿出课堂笔记，认真地复习课上学习的内容，他突然发现一道题∶ $(- x^{2} - 3 x y - \frac{1}{2} y^{2}) - (- \frac{1}{2} x^{2} - 4 x y - \frac{3}{2} y^{2}) = - \frac{1}{2} x^{2} . \dots + y^{2}$ ，这道题被墨水弄污了一部分，那么被弄污的地方应填（）

A、 $- 7 x y$ B、 $+ 7 x y$ C、 $- x y$ D、 $+ x y$

查看试题解析
9. 一台整式转化器原理如图，开始时输入关于x的整式M，当 $M = 2 x + 1$ 时，第一次输出 $4 x + 1$ ，继续下去，则第3次输出的结果是（　　）

A、 $16 x + 1$ B、 $14 x + 1$ C、 $12 x + 1$ D、 $8 x + 1$

查看试题解析
10. 已知甲，乙，丙，丁，戊五位同学依次取糖果，按先后顺序依次递减相同的量来取，正好取完.若丙同学取了15颗糖果，则共有糖果（）颗

A、75 B、70 C、65 D、60

查看试题解析

二、填空题（每空3分，共18分）

11. 不改变原式的值，把 $- 5 - (+ 2) - (- 6) + (- 2)$ 写成省略加号的和的形式为.

查看试题解析
12. －a－（b＋c）的相反数为．

查看试题解析
13. 当 $k =$ 时，代数式 $x^{6} - 5 k x^{4} y^{3} - 4 x^{6} + \frac{1}{5} x^{4} y^{3} + 10$ 中不含 $x^{4} y^{3}$ 项．

查看试题解析
14. 某同学把 $5 \times (□ - 6)$ 错抄为 $5 \times □ - 6$ ，若符合题意答案为 $m$ ，抄错后的结果为 $n$ ，则 $m - n =$ ．

查看试题解析
15. 如图，将边长为4的正方形和半径为2的圆叠放在一起，两个空白部分的面积分别为 $m ， n (m > n)$ ，则 $m - n$ 的值为（结果保留 $π$ ）.

查看试题解析
16. 甲、乙、丙三根木棒按如图所示的位置摆放在地面上．已知乙有一部分只与甲重叠，其余部分只与丙重叠，甲没有与乙重叠的部分的长度为 $3 m$ ，丙没有与乙重叠的部分的长度为 $5 m$ ．若甲的长度为 $a m$ ，乙的长度为 $b m$ ，则丙的长度为 $m$ ．（用含有 $a$ 、 $b$ 的代数式表示）

查看试题解析

三、计算题（共6题，共37分）

17. ﹣{﹣[+（﹣ $\frac{2}{3}$ ）]}.

查看试题解析
18. 计算：

(1)、 $(- 1) \times (- 4) + (- 9) \div 3 \times \frac{1}{3} + (- 2)$ ；

(2)、 $- 1^{2022} + {(- 2)}^{3} \times (- \frac{1}{2}) - | - 1 - 5 |$ ；

(3)、 $4 a^{3} - 3 a^{2} b + 5 {ab}^{2} + a^{2} b - 5 {ab}^{2} - 3 a^{3}$ ；

(4)、 $5 x^{2} - 7 x - [3 x^{2} - 2 (- x^{2} + 4 x - 1)]$ ．

查看试题解析
19. 先化简，再求值.
$2 (x y - x^{2}) - [(2 y^{2} + x^{2}) - 3 (x^{2} - 2 x y + y^{2})]$ ，其中 $x = - 1 ， y = \frac{1}{2}$ ；

查看试题解析
20. 已知多项式 $(x^{2} + m x - \frac{1}{2} y + 3) - (3 x - 2 y + 1 - n x^{2})$ .

(1)、若多项式的值与字母x的取值无关，求m、n的值；

(2)、在（1）的条件下，先化简多项式 $(3 m^{2} + m n + n^{2}) - 3 (m^{2} - m n - n^{2})$ ，再求它的值.

查看试题解析
21. 已知 $A = 3 a^{2} - 4 a b$ ， $B = a^{2} + 2 a b$ .

(1)、求 $A - 2 B$ ；

(2)、若 $| a + 1 | + {(2 - b)}^{2} = 0$ ，求 $A - 2 B$ 的值.

查看试题解析
22. 已知关于 $x$ 的多项式 $A$ ， $B$ ，其中 $A = m x^{2} + 2 x - 1$ ， $B = x^{2} - n x + 2$ （ $m$ ， $n$ 为有理数）.

(1)、化简 $2 B - A$ ；

(2)、若 $2 B - A$ 的结果不含 $x$ 项和 $x^{2}$ 项，求 $m$ 、 $n$ 的值.

查看试题解析

四、解答题（共6题，共45分）

23. 课堂上老师给大家出了这样一道题：“当 $x$ =2019时，求代数式 $(2 x^{3} - 3 x^{2} y - 2 x y^{2}) -$ $(x^{3} - 2 x y^{2} + y^{3}) +$ $(- x^{3} + 3 x^{2} y + y^{3})$ 的值”。小明一看，“ $x$ 的值太大了，又没有y的值，怎么算呢？”请帮小明解决这个问题，并写出具体过程。

查看试题解析
24. 学习了整式的加减运算后，郑老师出了一道题课堂练习题为“当 $a = - 2, b = 2016$ 时，求多项式 $3 a^{3} b^{3} - \frac{1}{2} a^{2} b + b - (4 a^{3} b^{3} + b - \frac{1}{4} a^{2} b - b^{2})$ + $(a^{3} b^{3} + \frac{1}{4} a^{2} b) - 2 b^{2} + 3$ 的值.”张同学把a=-2抄成a=2，韦同学没有抄错题，但他们做出的结果恰好一样，说说这是怎么回事？

查看试题解析

25. 阅读下面材料，并完成相应学习任务．晓彬同学在计算

2 (a b^{2} + 3 a^{2} b) - 3 (a b^{2} + a^{2} b)

时，写出如下计算步骤：

$2 (a b^{2} + 3 a^{2} b) - 3 (a b^{2} + a^{2} b)$

$= 2 a b^{2} + 6 a^{2} b - 3 a b^{2} - 3 a^{2} b$ 第一步

$= 2 a b^{2} - 3 a b^{2} + 6 a b^{2} - 3 a^{2} b$ 第二步

$= (2 a b^{2} - 3 a b^{2}) + (6 a^{2} b - 3 a^{2} b)$ 第三步

$= a b^{2} + 3 a^{2} b$ 第四步

(1)、任务一：

①以上步骤第一步是进行，此步骤用到的运算律是．

②第二步用到的运算律是，第三步用到的运算律是．

(2)、任务二：

①以上步骤第步出现了错误，错误的原因是．

请直接写出该整式正确的化简结果．

②计算：当 $a = - 1$ ， $b = 2$ 时，求该整式的值．

查看试题解析

26. 一个两位数，它的十位数字是x，个位数字是y.若把十位数字与个位数字对调，得到一个新的两位数.请回答下列问题：

(1)、分别用含x，y的代数式表示这个两位数和对调后的新的两位数.

(2)、计算新数与原数的差.根据计算结果，你会得到哪些结论？写出你最认可的一条.

查看试题解析
27. 如图，两叠规格相同的杯子整齐地叠放在桌面上，请根据图中给出的数据信息，解答下列问题：

(1)、按如图所示叠放一起时，相邻两个杯子杯口之间的高度相差cm.

(2)、若x个杯子按如图所示整齐叠放在桌面上，求这些杯子的顶部距离桌面的距离（用含x的代数式表示）.当 $x = 10$ 时，求这些杯子的顶部距离桌面的距离.

查看试题解析
28. 某公司生产一种电子产品和配件，已知该电子产品的售价为200元/台，配件的售价为20元/个，在促销活动期间，有如下两种优惠方案（顾客只能选择其中一种优惠方案）：
①买一台电子产品送一个配件；
②电子产品每台降价10元出售，配件每个打9折.
在促销活动期间，某学校计划到该公司购买 $x$ 台电子产品， $y$ 个配件 $(y > x > 0)$ .

(1)、分别求该校选择优惠方案①，②购买该电子产品和配件所需的总费用；（用含x、y的代数式来表示）

(2)、若该校计划购买该电子产品10台，配件20个，请通过计算判断，选择哪种优惠方案更省钱？

查看试题解析

2023年浙教版数学七年级上册4.6整式的加减 同步测试（提升版）

一、选择题（每题2分，共20分）

二、填空题（每空3分，共18分）

三、计算题（共6题，共37分）

四、解答题（共6题，共45分）

2023年浙教版数学七年级上册4.6整式的加减同步测试（提升版）