2023年浙教版数学七年级上册4.6整式的加减同步测试（培优版）

试卷更新日期：2023-09-02 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知多项式 $A = 2 （ m^{2} - 3 m n - n^{2} ）， B = m^{2} + 2 a m n + 2 n^{2} ，$ 若A-B中不含mn项，则a等于（）

A、-4 B、4 C、3 D、-3

查看试题解析
2. 若 $S = 3 x^{2} - 2 x y + y^{2}$ ， $T = x^{2} + 2 x y - y^{2}$ ，则 $S$ 与 $T$ 的大小关系为（）

A、 $S > T$ B、 $S < T$ C、 $S \geq T$ D、 $S \leq T$

查看试题解析
3. 若 $a 、 b 、 c 、 d$ 是正整数，且 $a + b = 20$ ， $a + c = 24$ ， $a + d = 22$ ，设 $a + b + c + d$ 的最大值为 $M$ ，最小值为 $N$ ，则 $M - N$ =（）

A、 $28$ B、 $12$ C、 $48$ D、 $36$

查看试题解析
4. 在“点燃我的梦想，数学皆有可衡”数学创新设计活动中，“智多星”小强设计了一个数学探究活动：对依次排列的两个整式m，n按如下规律进行操作：
第1次操作后得到整式串m，n， $n - m$ ；
第2次操作后得到整式串m，n， $n - m$ ， $- m$ ；
第3次操作后…
其操作规则为：每次操作增加的项，都是用上一次操作得到的最末项减去其前一项的差，小强将这个活动命名为“回头差”游戏．
则该“回头差”游戏第2023次操作后得到的整式中各项之和是（）

A、 $m + n$ B、m C、 $n - m$ D、 $2 n$

查看试题解析
5. 如图，将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形，并将①号、②号、③号正方形按图2方式叠放入④号正方形内部，若需求出阴影部分的周长和，只需知道下列哪个正方形的边长（）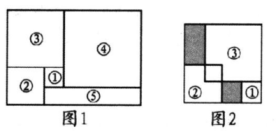

A、①号 B、②号 C、③号 D、④号

查看试题解析
6. 图1是长为 $a$ ，宽为 $b (a > b)$ 的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形 $A B C D$ 内，已知 $C D$ 的长度固定不变， $B C$ 的长度可以变化，图中阴影部分（即两个长方形）的面积分别表示为 $S_{1}$ ， $S_{2}$ ，若 $S = S_{1} - S_{2}$ ，且 $S$ 为定值，则 $a$ ， $b$ 满足的关系是（）

A、 $a = 2 b$ B、 $a = 3 b$ C、 $a = 4 b$ D、 $a = 5 b$

查看试题解析
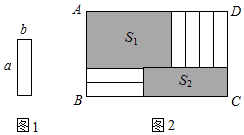7. 如图，将图1中的长方形纸片前成（1）号、（2）号、（3）号、（4）号正方形和（5）号长方形，并将它们按图2的方式无重叠地放入另一个大长方形中，若需求出没有覆盖的阴影部分的周长，则下列说法中错误的是（）

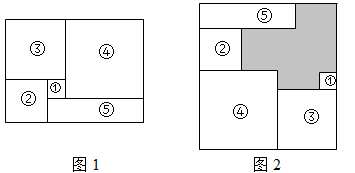A、只需知道图 1 中大长方形的周长即可 B、只需知道图 2 中大长方形的周长即可 C、只需知道（3）号正方形的周长即可 D、只需知道（5）号长方形的周长即可

查看试题解析
8. 将1，2，3，4...，60这60个自然数，任意分成30组，每组两个数，将每组的两个数中的任意一个数记做a，另一个数记做b，代入代数式 $\frac{1}{2}$ (|a-b|+a+b)中进行计算，求出结果，30组分别代入后可求出30个结果，则这30个值的和的最大值是（）

A、1365 B、1565 C、1735 D、1830

查看试题解析
9. 为求1+2+2²+2³+…+2²⁰¹⁵的值，可令S=1+2+2²+2³+…+2²⁰¹⁵ ，则2S=2+2²+2³+…+2²⁰¹⁶ ，因此2S﹣S=2²⁰¹⁶﹣1.仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹⁵的值为（）

A、5²⁰¹⁵﹣1 B、5²⁰¹⁶﹣1 C、 $\frac{5^{2015} - 1}{4}$ D、 $\frac{5^{2016} - 1}{4}$

查看试题解析
10. 将1，2，3，4，5，6六个数随机分成2组，每组各3个，分别用 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 和 $b_{1}$ ， $b_{2}$ ， $b_{3}$ 表示，且 $a_{1} < a_{2} < a_{3}$ ， $b_{1} > b_{2} > b_{3}$ ，设 $m = | a_{1} - b_{1} | + | a_{2} - b_{2} | + | a_{3} - b_{3} |$ ，则 $m$ 的可能值为（）.

A、 $3$ B、 $3 或 9$ C、 $9$ D、 $5 或 9$

查看试题解析

二、填空题（每空4分，共24分）

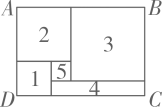
11. 如图长方形 $A B C D$ 由图1、2、3、4、5拼成，设图1、2、3是边长分别为a，b，c $(a < b < c)$ 的正方形，图4是长方形，图5是正方形．对于判断：① $a + b > c$ ；②图4的周长为 $3 b + c$ ；③ $a + c = 2 b$ ；④长方形 $A B C D$ 的周长为 $2 (a + b + c)$ ，其中正确的是（填编号）．

查看试题解析
12. 已知多项式 $A = a x^{2} + 2 x - 5 ， B = x^{2} - \frac{1}{2} b x$ ，且 $A - 2 B$ 的值与字母x的取值无关，则 $a^{2} - b^{2}$ 的值为．

查看试题解析
13. 2022年11月3 日，中国空间站“T”字基本构型在轨组装完成，“T”寓意：睿智，卓越．图1是用长方形纸板做成的四巧板(已知线段长度如图所示)，用它拼成图2的“T”字型图形，则“T”字型图形的周长为． (用含m，n的式子表示)

查看试题解析
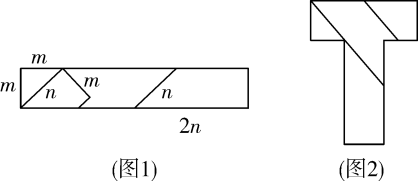14. 已知实数m，n，a，b满足 $m^{2} + a = b + 1 ， n^{2} + 2 b = 2 a + 4$ ，若 $k = m^{2} - 2 n^{2} + 3$ ，则k的取值范围是．

查看试题解析
15. 如图，用三个同（1）图的长方形和两个同（2）图的长方形用两种方式去覆盖一个大的长方形 $A B C D$ ，两种方式未覆盖的部分（阴影部分）的周长一样，那么（1）图中长方形的面积 $S_{1}$ 与（2）图长方形的面积 $S_{2}$ 的比是.

查看试题解析
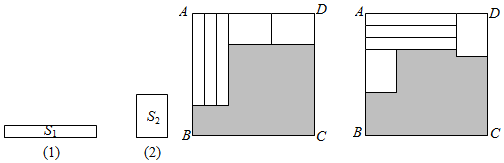16. 点 $A$ 、 $B$ 在数轴上分别表示有理数 $a$ 、 $b$ ，则在数轴上 $A$ 、 $B$ 两点之间的距离为 $A B = | a - b |$ ，利用数轴上两点间距离，可以得到 $| x + 1 | - | x - 3 |$ 的最大值是．

查看试题解析

三、解答题（共6题，共66分）

17. 已知A=2x²+3xy﹣2x﹣1，B=x²﹣xy﹣1.

(1)、化简：4A﹣（2B+3A），将结果用含有x、y的式子表示；

(2)、若式子4A﹣（2B+3A）的值与字母x的取值无关，求y³+ $\frac{7}{125}$ A﹣ $\frac{14}{125}$ B的值.

查看试题解析
18. 阅读材料：“整体思想”是中学数学解题中的一种重要的思想方法，如把某个多项式看成一个整体进行合理变形，它在多项式的化简与求值中应用极为广泛．例：化简 $4 (a + b) - 2 (a + b) + (a + b)$ ．解：原式 $= (4 - 2 + 1) (a + b)$ $= 3 (a + b)$ ．参照本题阅读材料的做法解答：

(1)、把 $(a - b)^{6}$ 看成一个整体，合并 $3 (a - b)^{6} - 5 (a - b)^{6} + 7 (a - b)^{6}$ 的结果是．

(2)、已知 $x^{2} - 2 y = 1$ ，求 $3 x^{2} - 6 y - 2021$ 的值．

(3)、已知 $a - 2 b = 2$ ， $2 b - c = - 5$ ， $c - d = 9$ ，求 $(a - c) + (2 b - d) - (2 b - c)$ 的值．

查看试题解析
19. 定义：若 $A - B = n$ ，则称A与B是关于数n的伴随数.比如4与3是关于1的伴随数， $2 x - 3$ 与 $2 x$ 是关于-3的伴随数.

(1)、填空： 2022与是关于-1的伴随数，与 $- 3 x + 5$ 是关于2的伴随数.

(2)、若a与2b是关于3的伴随数，2b与c是关于-5的伴随数，c与d是关于10的伴随数，求 $(a - c) + (2 b - d) - (2 b - c)$ 的值.

(3)、现有 $A = 8 x^{2} - 6 k x + 13$ 与 $B = 2 (4 x^{2} - 3 x + k)$ (k为常数)始终是数n的伴随数，求n的值.

查看试题解析
20. 有7张如图1规格相同的小长方形纸片，长为a，宽为b（ $a > b$ ），按如图2、3的方式不重叠无缝隙地放在矩形 $A B C D$ 内，未被覆盖的部分（两个矩形）用阴影表示．

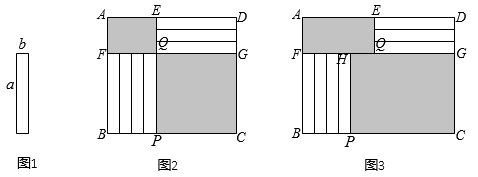(1)、如图2，点E、Q、P在同一直线上，点F、Q、G在同一直线上，那么矩形ABCD的面积为．（用含a、b的代数式表示）

(2)、如图3，点F、H、Q、G在同一直线上，设右下角与左上角的阴影部分的面积的差为S， $P C = x$ ．
①用a、b、x的代数式直接表示AE

②当BC的长度变化时，按照同样的放置方式，如果S的值始终保持不变，那么a、b必须满足什么条件？

查看试题解析
21. 已知口，⋆、△分别代表1∼9中的三个自然数．

(1)、如果用⋆△表示一个两位数，将它的个位和十位上的数字交换后得到一个新的两位数Δ⋆，若⋆Δ与Δ⋆的和恰好为某自然数的平方，则该自然数是；

(2)、如果在一个两位数⋆Δ前揷入一个数口后得到一个三位数口⋆△，设⋆△代表的两位数为x，口代表的数为y，则三位数口⋆Δ用含x，y的式子可表示为；

(3)、设a表示一个两位数，b表示一个三位数，把a放在b的左边组成一个五位数m，再把b放在a的左边、组成一个新五位数n．试探索：m-n能否被9整除？并说明你的理由．

查看试题解析
22. 阅读材料：
在数轴上 $A$ 点表示的数为 $a$ ， $B$ 点表示的数为 $b$ ，则点 $A$ 到点 $B$ 的距离记为 $A B$ ．线段 $A B$ 的长可以用右边的数减去左边的数表示，即 $A B = b - a$ ．

请用上面的知识解答下面的问题：

一个点从数轴上的原点开始，先向左移动1个单位长度到达 $A$ 点，再向左移动2个单位长度到达 $B$ 点，然后向右移动7个单位长度到达 $C$ 点．

(1)、 $A$ 点表示的数是； $B$ 点表示的数是； $C$ 点表示的数是；

(2)、点 $C$ 到点 $A$ 的距离 $C A =$ ；若数轴上有一点 $D$ ，且 $A D = 4$ ，则点 $D$ 表示的数为；

(3)、若将点 $A$ 向右移动 $x$ ，则移动后的点表示的数为；（用代数式表示）

(4)、若点 $B$ 以每秒2个单位长度的速度向左移动，同时 $A$ 、 $C$ 点分别以每秒1个单位长度.4个单位长度的速度向右移动．设移动时间为 $t$ 秒，试探索： $C A - A B$ 的值是否会随着 $t$ 的变化而改变？请说明理由．

查看试题解析

2023年浙教版数学七年级上册4.6整式的加减 同步测试（培优版）

一、选择题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共6题，共66分）

2023年浙教版数学七年级上册4.6整式的加减同步测试（培优版）