2019-2023高考数学真题分类汇编15 数列及等差数列

试卷更新日期：2023-09-02 类型：二轮复习

进入出卷网下载

一、选择题

1. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和．若 $a_{2} + a_{6} = 10 ， a_{4} a_{8} = 45$ ，则 $S_{5} =$ （）

A、25 B、22 C、20 D、15

查看试题解析
2. 已知等差数列 ${a_{n}}$ 的公差为 $\frac{2 π}{3}$ ，集合 $S = {c o s a_{n} | n \in N^{*}}$ ，若 $S = {a ， b}$ ，则 $a b =$ （）

A、－1 B、 $- \frac{1}{2}$ C、0 D、 $\frac{1}{2}$

查看试题解析
3. 中国的古建筑不仅是挡风遮雨的住处，更是美学和哲学的体现．如图是某古建筑物的剖面图， $D D_{1} ， C C_{1} ， B B_{1} ， A A_{1}$ 是举， $O D_{1} ， D C_{1} ， C B_{1} ， B A_{1}$ 是相等的步，相邻桁的举步之比分别为 $\frac{D D_{1}}{O D_{1}} = 0.5 ， \frac{C C_{1}}{D C_{1}} = k_{1} ， \frac{B B_{1}}{C B_{1}} = k_{2} ， \frac{A A_{1}}{B A_{1}} = k_{3}$ ，若 $k_{1} ， k_{2} ， k_{3}$ 是公差为0.1的等差数列，且直线 $O A$ 的斜率为0.725，则 $k_{3} =$ （）

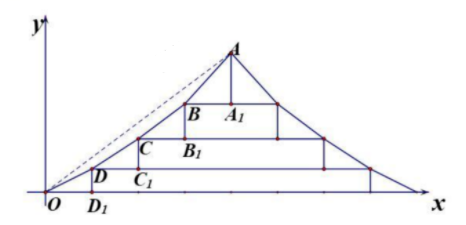A、0.75 B、0.8 C、0.85 D、0.9

查看试题解析
4. ${a_{n}}$ 和 ${b_{n}}$ 是两个等差数列，其中 $\frac{a_{k}}{b_{k}} (1 \leq k \leq 5)$ 为常值， $a_{1} = 288$ ， $a_{5} = 96$ ， $b_{1} = 192$ ，则 $b_{3} =$ （）

A、64 B、128 C、256 D、512

查看试题解析
5. 执行下面的程序框图，则输出的n=（）

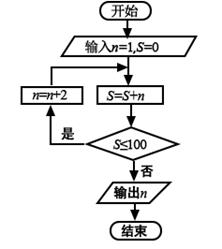A、17 B、19 C、21 D、23

查看试题解析
6. 北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板(称为天心石)，环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板(不含天心石)（）

A、3699块 B、3474块 C、3402块 D、3339块

查看试题解析
7. 在等差数列 ${a_{n}}$ 中， $a_{1} = - 9$ ， $a_{5} = - 1$ ．记 $T_{n} = a_{1} a_{2} \dots a_{n} (n = 1, 2, \dots)$ ，则数列 ${T_{n}}$ （）．

A、有最大项，有最小项 B、有最大项，无最小项 C、无最大项，有最小项 D、无最大项，无最小项

查看试题解析
8. 已知等差数列{a_n}的前n项和S_n ，公差d≠0， $\frac{a_{1}}{d}$ ≤1．记b₁＝S₂ ， b_n+1＝S_2n+2﹣S_2n ， n∈N*，下列等式不可能成立的是（）

A、2a₄＝a₂+a₆ B、2b₄＝b₂+b₆ C、a₄²＝a₂a₈ D、b₄²＝b₂b₈

查看试题解析
9. 记S_n为等差数列 ${a_{n}}$ 的前n项和。已知 $S_{4}$ =0， $a_{5}$ =5，则（）

A、a_n=2n-5 B、a_n=3n-10 C、S_n=2n²-8n D、S_n= $\frac{1}{2}$ n²-2n

查看试题解析
10. 已知数列{a_n}的前n项和为S_n= $\frac{1}{4}$ n²+ $\frac{2}{3}$ n+3(n∈N*)，则下列结论正确的是（）

A、数列{a_n}是等差数列 B、数列{a_n}是递增数列 C、a₁ ， a₅ ， a₉成等差数列 D、S₆-S₃ ， S₉-S₆ ， S₁₂-S₉成等差数列

查看试题解析
11. 数列 ${a_{n}}$ 是递增的整数数列，且 $a_{1} \geq 3$ ， $a_{1} + a_{2} + \cdot \cdot \cdot + a_{n} = 100$ ，则 $n$ 的最大值为（）

A、9 B、10 C、11 D、12

查看试题解析

二、填空题

12. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前n项和．若 $2 S_{3} = 3 S_{2} + 6$ ，则公差 $d =$ ．

查看试题解析
13. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前n项和．若 $a_{1} = - 2, a_{2} + a_{6} = 2$ ，则 $S_{10} =$ ．

查看试题解析
14. 已知数列 ${a_{n}} (n \in N^{*})$ 是等差数列， $S_{n}$ 是其前n项和.若 $a_{2} a_{5} + a_{8} = 0, S_{9} = 27$ ，则 $S_{8}$ 的值是.

查看试题解析
15. 记S_n为等差数列{a_n}的前n项和，若 $a_{3} = 5, a_{7} = 13$ ，则 $S_{10} =$ .

查看试题解析
16. 记S_n为等差数列{a_n}项和，若a₁≠0，a₂=3a₁ ，则 $\frac{S_{10}}{S_{5}}$ =。

查看试题解析
17. 设等差数列{a_n}的前n项和为S_n.若a₂=-3，S₅=-10，则a₅= ， S_n的最小值为.

查看试题解析

三、解答题

18. 记 $S_{n}$ 是公差不为0的等差数列 ${a_{n}}$ 的前n项和，若 $a_{3} = S_{5}, a_{2} a_{4} = S_{4}$ ．

(1)、求数列 ${a_{n}}$ 的通项公式 $a_{n}$ ；

(2)、求使 $S_{n} > a_{n}$ 成立的n的最小值．

查看试题解析
19. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和，已知 $a_{2} = 11 ， S_{10} = 40$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、求数列 ${| a_{n} |}$ 的前 $n$ 项和 $T_{n}$ ．

查看试题解析
20. 已知 ${a_{n}}$ 为等差数列， $b_{n} = {\begin{cases} a_{n} - 6 ， n 为奇数 \\ 2 a_{n} ， n 为偶数 \end{cases}$ ，记 $S_{n}$ ， $T_{n}$ 为 ${a_{n}}$ ${b_{n}}$ 的前n项和， $S_{4} = 32$ ， $T_{3} = 16$

(1)、求 ${a_{n}}$ 的通项公式.

(2)、证明：当n>5时， $T_{n}$ > $S_{n}$ .

查看试题解析
21. 记 $S_{n}$ 为数列 ${a_{n}}$ 的前n项和，已知 $a_{1} = 1 ， {\frac{S_{n}}{a_{n}}}$ 是公差为 $\frac{1}{3}$ ，的等差数列.

(1)、求 ${a_{n}}$ 的通项公式；

(2)、证明： $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \dots + \frac{1}{a_{n}} < 2$

查看试题解析
22. 记 $S_{n}$ 为 ${a_{n}}$ 的前 $n$ 项和，已知 $a_{n} > 0 ， a_{2} ＝ 3 a_{1}$ ，且数列 ${\sqrt{S_{n}}}$ 是等差数列．证明： ${a_{n}}$ 是等差数列．

查看试题解析
23. 记S_n为数列{a_n}的前n项和，b_n为数列{S_n}的前n项积，已知 $\frac{2}{S_{n}} + \frac{1}{b_{n}}$ =2.

(1)、证明：数列{b_n}是等差数列；

(2)、求{a_n}的通项公式.

查看试题解析
24. 已知数列{ $a_{n}$ }满足 $a_{1}$ =1， $a_{n + 1} = {\begin{matrix} a_{n} + 1 ， n 为奇数 \\ a_{n} + 2 ， n 为偶数 \end{matrix}$

(1)、记 $b_{n}$ = $a_{2 n}$ ，写出 $b_{1}$ ， $b_{2}$ ，并求数列 ${b_{n}}$ 的通项公式；

(2)、求 ${a_{n}}$ 的前20项和

查看试题解析
25. 设{a_n}是等差数列，a₁=-10，且a₂+10，a₃+8，a₄+6成等比数列.
（I）求{a_n}的通项公式；

（Ⅱ）记{a_n}的前n项和为S_n ，求S_n的最小值.

查看试题解析
26. 记S_n为等差数列{a_n}的前n项和，已知S_n=-a₅

(1)、若a₃=4，求{a_n}的通项公式。

(2)、若a₁≥0，求使得S_n≥a_n的n取值范围。

查看试题解析
27. 已知数列{a_n｝的各项均为正数，记S_n为{a_n｝的前n项和，从下面①②③中选取两个作为条件，证明另外一个成立.
①数列{a_n｝是等差数列：②数列{ $\sqrt{S_{n}}$ ｝是等差数列；③a₂=3a₁

注：若选择不同的组合分别解答，则按第一个解答计分.

查看试题解析