2023年浙教版数学七年级上册4.5合并同类项 同步测试(培优版)
试卷更新日期:2023-09-02 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 若单项式与的和仍是单项式,则的值是( )A、6 B、4 C、9 D、82. 算式的结果是( )A、 B、 C、 D、3. 若单项式与单项式的和仍为单项式,则的值为( )A、6 B、1 C、3 D、4. 若多项式可以进一步合并同类项,则 , 的值分别是( )A、 , B、 , C、 , D、 ,5. 如果单项式与的和是单项式,那么的值为( )A、 B、0 C、-1 D、16. ( )A、 B、 C、 D、7. 数轴上,有理数a、b、-a、c的位置如图,则化简的结果为( )
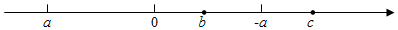 A、 B、 C、 D、08. 若等式□成立,则□填写单项式可以是( )A、a B、 C、 D、9. 如图,从标有单项式的四张卡片中找出所有能合并的同类项,若它们合并后的结果为 , 则代数式的值为( )
A、 B、 C、 D、08. 若等式□成立,则□填写单项式可以是( )A、a B、 C、 D、9. 如图,从标有单项式的四张卡片中找出所有能合并的同类项,若它们合并后的结果为 , 则代数式的值为( )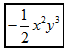
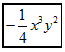
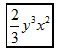
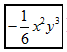 A、-1 B、0 C、1 D、210. 我国古代许多关于数学的发现都曾位居世界前列,其中“杨辉三角”就是一例,它给出了(为正整数)的展开式(按的次数由大到小的顺序排列)的系数规律.例如,第三行的四个数1,3,3,1恰好对应着展开式中各项的系数.请你猜想的展开式中与含项的系数相同的项的同类项是( )
A、-1 B、0 C、1 D、210. 我国古代许多关于数学的发现都曾位居世界前列,其中“杨辉三角”就是一例,它给出了(为正整数)的展开式(按的次数由大到小的顺序排列)的系数规律.例如,第三行的四个数1,3,3,1恰好对应着展开式中各项的系数.请你猜想的展开式中与含项的系数相同的项的同类项是( )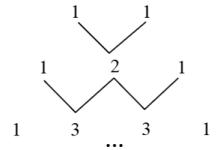 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空4分,共24分)
-
11. 若单项式与单项式的和仍是单项式,则 .12. 若单项式 与 是同类项,则 的值是.13. 若与是同类项,则的平方根是 .14. 如果单项式与单项式是同类项,那么代数式.15. 已知a,b,c三个有理数在数轴上对应的位置如图所示,化简|c-a|-|a-b|-|b|=.
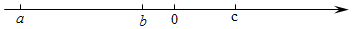 16. 如图,用正方形方框在日历中任意框出4个数,设其中最小的数为x,那么这4个数之和为 .
16. 如图,用正方形方框在日历中任意框出4个数,设其中最小的数为x,那么这4个数之和为 .星期一
星期二
星期三
星期四
星期五
星期六
星期日
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
三、解答题(共8题,共66分)
-
17.(1)、计算:(2)、合并同类项:18. 化简:19. 化简多项式 , 当 , 时,求该多项式的值.20. 若多项式mx3﹣2x2+4x﹣3﹣3x3+6x2﹣nx+6化简后不含x的三次项和一次项,请你求m、n的值,并求出(m﹣n)2021的值.21. 已知:实数、、在数轴上的位置如图:且 , 化简:.
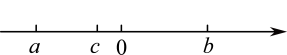 22.(1)、已知2x2+ax-y+6-2bx2+3x-5y-1的值与x的取值无关,求a3-2b2的值.(2)、已知关于x的四次三项式ax4-(a-12)x3-(b+3)x2-bx+11中不含x3及x2项,试写出这个多项式,并求当x=-1时,这个多项式的值.
22.(1)、已知2x2+ax-y+6-2bx2+3x-5y-1的值与x的取值无关,求a3-2b2的值.(2)、已知关于x的四次三项式ax4-(a-12)x3-(b+3)x2-bx+11中不含x3及x2项,试写出这个多项式,并求当x=-1时,这个多项式的值.