2023年浙教版数学七年级上册4.3代数式的值同步测试（培优版）

试卷更新日期：2023-09-02 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共24分）

1. 已知 $a - 2 b = - 1$ ，则代数式 $1 - 2 a + 4 b$ 的值是（）

A、-3 B、-1 C、2 D、3

查看试题解析
2. 已知 $x + y = - 1010$ ，则代数式 $3 - 2 x - 2 y$ 的值为（）

A、2023 B、-2021 C、2021 D、-2023

查看试题解析
3. 若 $x^{2} + 3 x - 5$ 的值为 $7$ ，则 $3 x^{2} + 9 x - 2$ 的值为（）

A、44 B、34 C、24 D、14

查看试题解析
4. 按如图所示的运算程序，能使输出 $y$ 值为 $5$ 的是（）

A、 $m = 2$ ， $n = 1$ B、 $m = 2$ ， $n = 0$ C、 $m = 2$ ， $n = 2$ D、 $m = 3$ ， $n = 2$

查看试题解析
5. 若 $a + b = 7$ ， $c - d = 4$ ，则 $(b + c) - (d - a)$ 的值是（）

A、11 B、-11 C、3 D、-3

查看试题解析
6. 当 $x = 1$ 时，代数式 $p x^{3} + q x + 1$ 的值为2023，则当 $x = - 1$ 时，代数式 $p x^{3} + q x + 1$ 的值为（）

A、 $- 2019$ B、 $- 2021$ C、2022 D、2023

查看试题解析
7. 按下面的运算程序计算：
当输入 $n = 6$ 时，输出结果为33；当输入 $n = 7$ 时，输出结果为17．如果输入n的值为正整数，输出的结果为25，那么满足条件的n的值最多有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图是一个数值转换机的示意图，若输入x的值为3，y的值为-2，则输出的结果为（）

A、-6 B、5 C、-5 D、6

查看试题解析

二、填空题（每空4分，共28分）

9. 在数轴上表示数a的点到原点的距离为6，则 $a + | - a | ＝$ .

查看试题解析
10. 已知有理数x，y，数 $| x | = 3$ ， $| y | = 2$ ，且 $x < 0 < y$ ，则 $x^{y} =$ ．

查看试题解析
11. 已知有理数 $a$ 、 $b$ 互为相反数， $c$ 、 $d$ 互为倒数， $| m | = 4$ ，则 $2 a - 5 c d - m + 2 b$ 的值为．

查看试题解析
12. 当x＝1时，代数式19ax³-7bx-13的值为13，则x＝-1时，19ax³-7bx-13的值为.

查看试题解析
13. 历史上数学家欧拉最先把关于x的多项式用记号 $f (x)$ 来表示，把x等于某数a时的多项式的值用 $f (a)$ 来表示.例如，对于多项式 $f (x) = m x^{3} + n x + 5$ ，当 $x = 2$ 时，多项式的值为 $f (2) = 8 m + 2 n + 5$ .若对于多项式 $f (x) = t x^{5} + m x^{3} + n x + 7$ ，有 $f (3) = 6$ ，则 $f (- 3)$ 的值为.

查看试题解析
14. 如果x取任意值，等式（2x+3）⁴＝a₀x⁴+a₁x³+a₂x²+a₃x+a₄都成立，那么，

(1)、a₄＝；

(2)、a₀-a₁+a₂-a₃+a₄＝．

查看试题解析

三、解答题（共9题，共68分）

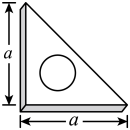
15. 已知a，b互为相反数，c，d互为倒数， $| m | = 2$ 求 $3 (a + b - 1) + (- c d)^{2022} - 2 m$ 的值．

查看试题解析
16. 已知x、y互为相反数，m、n互为倒数，且|a|=7，试求下面代数式的值：a²-（x+y+mn）a+x²⁰²¹+y²⁰²¹-（-mn）²⁰¹⁹ ．

查看试题解析
17. 一块三角尺的形状和尺寸如图所示，如果圆孔的半径是r，三角尺的厚度是h，用式子表示这块三角尺的体积V．若 $a = 6 c m ， r = 0.5 c m ， h = 0.2 c m$ ，求V的值（ $π$ 取3）．

查看试题解析
18. 如图，用代数式表示正方形中阴影部分的面积，并求出 $a ＝ 2$ ， $b ＝ 1$ 时阴影部分的面积是多少？（π取3）

查看试题解析
19. 为了节约用水，某市规定三口之家每月标准用水量为 $15$ 立方米，超过部分加价收费，假设不超过部分水费为 $1.5$ 元 $/$ 立方米，超过部分水费为 $3$ 元/立方米．

(1)、如果甲、乙两家用水量分别为 $10$ 立方米和 $20$ 立方米，那么甲、乙两家该月应各交多少水费？

(2)、当每月用水量为 $a$ 立方米时，请用代数式分别表示这家按标准用水量和超出标准用水时各应缴纳的水费；

(3)、当丁家本月交水费 $46.5$ 元时，那么丁家该月用水多少立方米？

查看试题解析
20. 某商场销售一种乒乓球拍和乒乓球，乒乓球拍每副定价 $80$ 元，乒乓球每盒定价 $20$ 元，“国庆节”假期期间商场决定开展促销活动，活动期间向客户提供两种优惠方案.
方案一：买一副乒乓球拍送一盒乒乓球；
方案二：乒乓球拍和乒乓球都按定价的 $90 %$ 付款.
某客户要到该商场购买乒乓球拍 $20$ 副，乒乓球 $x$ 盒（ $x > 20$ 且为整数）.

(1)、用含 $x$ 的代数式表示按两种方案购买各需付款多少元？

(2)、若 $x = 30$ ，通过计算说明此时按哪种方案购买较合算；

(3)、当 $x = 30$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法.

查看试题解析
21. 近日，教育部印发《义务教育课程方案》和课程标准（2022年版），将劳动从原来的综合实践活动课程中独立出来.海南华侨中学初中部为了让学生体验农耕劳动，开辟了一处耕种园，需要采购一批某种菜苗开展种植活动.已知甲、乙两菜苗基地该种菜苗每捆的标价都是2元（菜苗的质量一样好），但甲、乙两菜苗基地的优惠条件却不同.
甲菜苗基地：若购买不超过10捆，则按标价付款；若一次购10捆以上，则超过10捆的部分按标价的 $60 %$ 付款.
乙菜苗基地：按标价的 $80 %$ 付款.

(1)、若学校决定购买该种菜苗15捆，则在甲菜苗基地购买，需付款元，在乙菜苗基地购买，需付款元；

(2)、若学校决定购买该种菜苗x捆（ $x > 10$ ），请用含x的式子分别表示在甲、乙两个菜苗基地购买该种菜苗的费用；

(3)、若学校决定购买该种菜苗30捆，你认为在甲、乙两菜苗基地中，到哪个菜苗基地购买比较省钱?说明理由.

查看试题解析
22. 某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元，在促销活动期间，该厂向客户提供了两种优惠方案(客户只能选择其中一种优惠方案)：
①买一套西装送一条领带；

②西装按原价的9折收费，领带按原价的8折收费．

在促销活动期间，某客户要到该服装厂购买x套西装，y条领带(y>x)．

(1)、该客户选择两种不同的方案所需总费用分别是多少元？ (用含x y的式子表示并化简)

(2)、若该客户需要购买10套西装，22条领带，则他选择哪种方案更划算？

(3)、若该客户需要购买15套西装，40条领带，则他选择哪种方案更划算？

查看试题解析
23. 有这样一道题“如果代数式 $5 a + 3 b$ 的值为-4，那么代数式 $2 (a + b) + 4 (2 a + b)$ 的值是多少？”爱动脑筋的汤同学解题过程如下：
原式 $= 2 a + 2 b + 8 a + 4 b = 10 a + 6 b = 2 (5 a + 3 b) = 2 \times (- 4) = - 8$ .

汤同学把 $5 a + 3 b$ 作为一个整体求解整体思想是中学数学解题中的一种重要思想方法，请仿照上面的解题方法，完成下面问题：

（简单应用）

(1)、已知 $a^{2} + a = 3$ ，则 $2 a^{2} + 2 a + 2021 =$ ；

(2)、已知 $a - 2 b = - 3$ ，求 $3 (a - b) - 7 a + 11 b + 5$ 的值；

(3)、（拓展提高）
已知 $a^{2} + 2 a b = - 5$ ， $a b - 2 b^{2} = - 3$ ，求代数式 $2 a^{2} + \frac{5}{2} a b + 3 b^{2}$ 的值.

查看试题解析

2023年浙教版数学七年级上册4.3代数式的值 同步测试（培优版）

一、选择题（每题3分，共24分）

二、填空题（每空4分，共28分）

三、解答题（共9题，共68分）

2023年浙教版数学七年级上册4.3代数式的值同步测试（培优版）