2019-2023高考数学真题分类汇编12 简单逻辑用语、基本不等式、不等式
试卷更新日期:2023-09-02 类型:二轮复习
一、选择题
-
1. “为整数”是“为整数”的()A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件2. 已知 是定义在上 的函数,那么“函数 在 上单调递增”是“函数 在 上的最大值为 ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 已知命题p: x∈R,sinx<1;命题q: x∈R, e|x|≥1,则下列命题中为真命题的是( )A、p q B、 p q C、p q D、 (pVq)4. 已知 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不允分也不必要条件5. 若a>0,b>0,则“a+b≤4“是“ab≤4”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件6. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件7. “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分又不必要条件8. 若 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件9. 已知 、 ,则“ ”是“ ”的( )
A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分又非必要条件10. 记不等式组 表示的平面区域为D.命题 ;命题 .下面给出了四个命题( )① ② ③ ④
这四个命题中,所有真命题的编号是( )
A、①③ B、①② C、②③ D、③④11. 设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则( )A、 (log3 )> ( )> ( ) B、 (log3 )> ( )> ( ) C、 ( )> ( )> (log3 ) D、 ( )> ( )> (log3 )12. 设函数f(x)=cosx+bsinx(b为常数),则“b=0”是“f(x)为偶函数”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件13. 一元二次不等式x(9-x)>0的解集是( )A、{x|x<0或x>9} B、{x|0<x<9} C、{x|x<-9或x>0} D、{x|-9<x<0}14. 已知x,y是实数,则“x+y≤1”是“x≤ 或y≤ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件二、多项选择题
-
15. 对任意x,y, ,则( )A、 B、 C、 D、16. 已知a>0,b>0,且a+b=1,则( )A、 B、 C、 D、
三、填空题
-
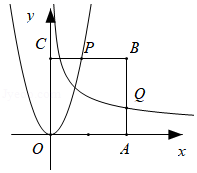
17. 若 ,则 的最小值为 .18. 已知 ,且 ,则 的最小值为 .19. 设 ,使不等式 成立的 的取值范围为.20. 已知 中,点D在边BC上, .当 取得最小值时, .21. 已知 ,则 的最小值是 .22. 如图,已知正方形 ,其中 ,函数 交 于点 ,函数 交 于点 ,当 最小时,则 的值为 .