【备考2024】广西数学中考十年回顾6 探索数、式、图的规律
试卷更新日期:2023-09-02 类型:二轮复习
一、选择题
-
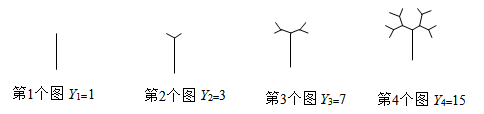
1. 观察下列按一定规律排列的n个数:2,4,6,8,10,12,…;若最后三个数之和是3000,则n等于( )A、499 B、500 C、501 D、10022. 定义一种运算: ,则不等式 的解集是( )A、 或 B、 C、 或 D、 或3. 观察下列树枝分杈的规律图,若第n个图树枝数用 表示,则 ( )
 A、 B、 C、 D、4. 定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=-1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i-9=-8+6i,因此,(1+3i)2的实部是-8,虚部是6.已知复数(3-mi)2的虚部是12,则实部是( )A、-6 B、6 C、5 D、-55. 计算 + + + +…+ 的结果是( )A、 B、 C、 D、6. 定义新运算:p⊕q= ,例如:3⊕5= ,3⊕(﹣5)= ,则y=2⊕x(x≠0)的图象是( )
A、 B、 C、 D、4. 定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=-1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i-9=-8+6i,因此,(1+3i)2的实部是-8,虚部是6.已知复数(3-mi)2的虚部是12,则实部是( )A、-6 B、6 C、5 D、-55. 计算 + + + +…+ 的结果是( )A、 B、 C、 D、6. 定义新运算:p⊕q= ,例如:3⊕5= ,3⊕(﹣5)= ,则y=2⊕x(x≠0)的图象是( )
A、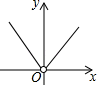 B、
B、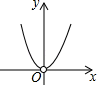 C、
C、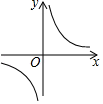 D、
D、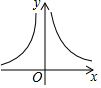 7. 对任意实数a,b定义运算“∅”:a∅b= ,则函数y=x2∅(2﹣x)的最小值是( )A、﹣1 B、0 C、1 D、48. 按一定规律排列的一列数依次为:2,3,10,15,26,35,…,按此规律排列下去,则这列数中的第 100 个数是( )A、9999 B、10000 C、10001 D、100029. 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为( )
7. 对任意实数a,b定义运算“∅”:a∅b= ,则函数y=x2∅(2﹣x)的最小值是( )A、﹣1 B、0 C、1 D、48. 按一定规律排列的一列数依次为:2,3,10,15,26,35,…,按此规律排列下去,则这列数中的第 100 个数是( )A、9999 B、10000 C、10001 D、100029. 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为( )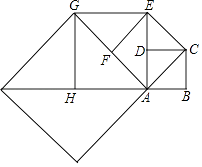 A、( )n﹣1 B、2n﹣1 C、( )n D、2n10. 观察以下一列数的特点:0,1,﹣4,9,﹣16,25,…,则第11个数是( )A、﹣121 B、﹣100 C、100 D、12111. 将一组数 ,2, ,2 , ,…,2 ,按下列方式进行排列:
A、( )n﹣1 B、2n﹣1 C、( )n D、2n10. 观察以下一列数的特点:0,1,﹣4,9,﹣16,25,…,则第11个数是( )A、﹣121 B、﹣100 C、100 D、12111. 将一组数 ,2, ,2 , ,…,2 ,按下列方式进行排列:,2, ,2 , ;
2 , ,4,3 ,2 ;
…
若2的位置记为(1,2),2 的位置记为(2,1),则 这个数的位置记为( )
A、(5,4) B、(4,4) C、(4,5) D、(3,5)12. 一列数a1 , a2 , a3 , …,其中a1= ,an= (n为不小于2的整数),则a100=( )A、 B、2 C、﹣1 D、﹣213. 2615个位上的数字是( )A、2 B、4 C、6 D、814. 如图,在平面直角坐标系中,直线l:y= x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A5B6A6的周长是( ) A、24 B、48 C、96 D、19215. 直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk , 当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200=( )A、10000 B、10050 C、10100 D、1015016.
A、24 B、48 C、96 D、19215. 直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk , 当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200=( )A、10000 B、10050 C、10100 D、1015016.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
 A、(﹣1,0) B、(1,﹣2) C、(1,1) D、(﹣1,﹣1)17.
A、(﹣1,0) B、(1,﹣2) C、(1,1) D、(﹣1,﹣1)17.相传古印度一座梵塔圣殿中,铸有一片巨大的黄铜板,之上树立了三米高的宝石柱,其中一根宝石柱上插有中心有孔的64枚大小两两相异的一寸厚的金盘,小盘压着较大的盘子,如图,把这些金盘全部一个一个地从1柱移到3柱上去,移动过程不许以大盘压小盘,不得把盘子放到柱子之外.移动之日,喜马拉雅山将变成一座金山.
设h(n)是把n个盘子从1柱移到3柱过程中移动盘子之最少次数
n=1时,h(1)=1;
n=2时,小盘→2柱,大盘→3柱,小盘从2柱→3柱,完成.即h(2)=3;
n=3时,小盘→3柱,中盘→2柱,小盘从3柱→2柱.[即用h(2)种方法把中、小两盘移到2柱,大盘3柱;再用h(2)种方法把中、小两盘从2柱3柱,完成;
我们没有时间去移64个盘子,但你可由以上移动过程的规律,计算n=6时,h(6)=( )
 A、11 B、31 C、63 D、12718. 如 ,我们叫集合 ,其中1,2, 叫做集合 的元素.集合中的元素具有确定性(如 必然存在),互异性(如 , ),无序性(即改变元素的顺序,集合不变).若集合 ,我们说 .已知集合 ,集合 ,若 ,则 的值是( )A、-1 B、0 C、1 D、2
A、11 B、31 C、63 D、12718. 如 ,我们叫集合 ,其中1,2, 叫做集合 的元素.集合中的元素具有确定性(如 必然存在),互异性(如 , ),无序性(即改变元素的顺序,集合不变).若集合 ,我们说 .已知集合 ,集合 ,若 ,则 的值是( )A、-1 B、0 C、1 D、2二、填空题
-
19. 我们规定:若 ,则 .例如 ,则 .已知 ,且 ,则 的最大值是.20. 如图,直线l的函数表达式为y=x﹣1,在直线l上顺次取点A1(2,1),A2(3,2),A3(4,3),A4(5,4),…,An(n+1,n),构成形如
 ”的图形的阴影部分面积分别表示为S1 , S2 , S3 , …,Sn , 则S2021=.
”的图形的阴影部分面积分别表示为S1 , S2 , S3 , …,Sn , 则S2021=. 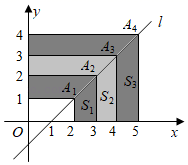 21. 如图,每一幅图中有若干个菱形,第1幅图中有1个菱形,第2幅图中有3菱形.第3幅图中有5个菱形,依照此规律,第6幅图中有个菱形.
21. 如图,每一幅图中有若干个菱形,第1幅图中有1个菱形,第2幅图中有3菱形.第3幅图中有5个菱形,依照此规律,第6幅图中有个菱形.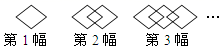 22. 如图,在矩形ABCD中,AB=8,BC=4,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着PR方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与矩形的边碰撞次数经过2019次后,则它与AB边的碰撞次数是.
22. 如图,在矩形ABCD中,AB=8,BC=4,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着PR方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与矩形的边碰撞次数经过2019次后,则它与AB边的碰撞次数是.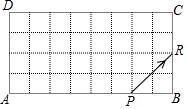 23. 观察一列数: ,0,3,6,9,12,…,按此规律,这一列数的第21个数是.24. a1 , a2 , a3 , a4 , a5 , a6 , …,是一列数,已知第1个数a1=4,第5个数a5=5,且任意三个相邻的数之和为15,则第2019个数a2019的值是.25. 观察以下一列数:3, , , , ,…则第20个数是 .26. 将从1开始的连续自然数按右图规律排列:
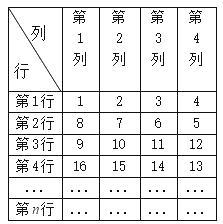
23. 观察一列数: ,0,3,6,9,12,…,按此规律,这一列数的第21个数是.24. a1 , a2 , a3 , a4 , a5 , a6 , …,是一列数,已知第1个数a1=4,第5个数a5=5,且任意三个相邻的数之和为15,则第2019个数a2019的值是.25. 观察以下一列数:3, , , , ,…则第20个数是 .26. 将从1开始的连续自然数按右图规律排列:规定位于第m行,第n列的自然数10记为(3,2),自然数15记为(4,2)......按此规律,自然数2018记为
 27. 如图,直线l为y= x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1 , 以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2 , 以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为().
27. 如图,直线l为y= x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1 , 以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2 , 以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(). 28. 将从1开始的连续自然数按一下规律排列:
28. 将从1开始的连续自然数按一下规律排列:第1行
1
第2行
2
3
4
第3行
9
8
7
6
5
第4行
10
11
12
13
14
15
16
第5行
25
24
23
22
21
20
19
18
17
…
则2017在第行.
29. 有这样一组数据a1 , a2 , a3 , …an , 满足以下规律: (n≥2且n为正整数),则a2013的值为(结果用数字表示).30.如图是三种化合物的结构式及分子式.请按其规律,写出后面第2013种化合物的分子式 .
 31.
31.如图,下列图案都是由小正方形组成的,它们形成矩形的个数是有规律的:第(1)个图案中,矩形的个数是1个;第(2)个图案中,矩形的个数是4个;…第(25)个图案中,矩形的个数是个.
 32. 甲、乙、丙三位同学进行报数游戏,游戏规则为:甲报1,乙报2,丙报3,再甲报4,乙报5,丙报6,…依次循环反复下去,当报出的数为2014时游戏结束,若报出的数是偶数,则该同学得1分.当报数结束时甲同学的得分是分.33. 观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则81+82+83+84+…+82014的和的个位数字是 .34. 已知点A1(a1 , a2),A2(a2 , a3),A3(a3 , a4)…,An(an , an+1)(n为正整数)都在一次函数y=x+3的图象上.若a1=2,则a2014= .35. 观察以下等式:32﹣12=8,52﹣12=24,72﹣12=48,92﹣12=80,…由以上规律可以得出第n个等式为 .36. 如图是小强用铜币摆放的4个图案,根据摆放图案的规律,试猜想第n个图案需要个铜币.
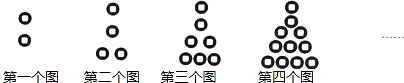
32. 甲、乙、丙三位同学进行报数游戏,游戏规则为:甲报1,乙报2,丙报3,再甲报4,乙报5,丙报6,…依次循环反复下去,当报出的数为2014时游戏结束,若报出的数是偶数,则该同学得1分.当报数结束时甲同学的得分是分.33. 观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则81+82+83+84+…+82014的和的个位数字是 .34. 已知点A1(a1 , a2),A2(a2 , a3),A3(a3 , a4)…,An(an , an+1)(n为正整数)都在一次函数y=x+3的图象上.若a1=2,则a2014= .35. 观察以下等式:32﹣12=8,52﹣12=24,72﹣12=48,92﹣12=80,…由以上规律可以得出第n个等式为 .36. 如图是小强用铜币摆放的4个图案,根据摆放图案的规律,试猜想第n个图案需要个铜币.
 37.
37.观察下列等式:
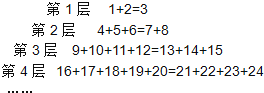
在上述数字宝塔中,从上往下数,2016在第层.
38. 我们把分子为1的分数叫做理想分数,如 , , ,…,任何一个理想分数都可以写成两个不同理想分数的和,如 = + ; = + ; = + ;…根据对上述式子的观察,请你思考:如果理想分数 (n是不小于2的正整数)= ,那么a+b= . (用含n的式子表示)