2019-2023高考数学真题分类汇编6 函数的导数及其应用（2）

试卷更新日期：2023-09-02 类型：二轮复习

进入出卷网下载

一、选择题

1. 函数 $f (x) = x^{4} - 2 x^{3}$ 的图像在点 $(1 ， f (1))$ 处的切线方程为（）

A、 $y = - 2 x - 1$ B、 $y = - 2 x + 1$ C、 $y = 2 x - 3$ D、 $y = 2 x + 1$

查看试题解析
2. 设 $a = 0.1 e^{0.1} ， b = \frac{1}{9} ， c = - ln 0.9 ，$ 则（）

A、 $a < b < c$ B、 $c < b < a$ C、 $c < a < b$ D、 $a < c < b$

查看试题解析
3. 若函数 $f (x) = e^{x} - a x^{2} - 2 a x$ 有两个极值点，则实数 $a$ 的取值范围为（）

A、 $(- \frac{1}{2} ， 0)$ B、 $(- \infty ， - \frac{1}{2})$ C、 $(0 ， \frac{1}{2})$ D、 $(\frac{1}{2} ， + \infty)$

查看试题解析
4. 若过点（a,b)可以作曲线y=e^x的两条切线，则（）

A、e^b<a B、e^a<b C、0<a<e^b D、0<b<e^a

查看试题解析
5. 已知曲线y=ae^x+xlnx在点（1，ae）处的切线方程为y=2x+b，则（）

A、a=e，b=-1 B、a=e，b=1 C、a=e^-1 ， b=1 D、a=e^-1 ， b=-1

查看试题解析
6. 曲线y=2sinx+cosx在点（π，-1）处的切线方程为（）

A、x-y-π-1=0 B、2x-y-2π-1=0 C、2x+y-2π+1=0 D、x+y-π+1=0

查看试题解析
7. 设a≠0，若x=a为函数 $f (x) = a {(x - a)}^{2} (x - b)$ 的极大值点，则（）

A、a＜b B、a＞b C、ab＜a² D、ab＞a²

查看试题解析
8. 已知 $a \in R$ ，设函数 $f (x) = {\begin{array}{l} x^{2} - 2 a x + 2 a, & x ⩽ 1, \\ x - a \ln x, & x > 1, \end{array}$ 若关于 $x$ 的不等式 $f (x) ⩾ 0$ 在 $R$ 上恒成立，则 $a$ 的取值范围为（）

A、 $[0, 1]$ B、 $[0, 2]$ C、 $[0, e]$ D、 $[1, e]$

查看试题解析

二、多项选择题

9. 已知函数 $f (x)$ 及其导函数 $f^{'} (x)$ 的定义域均为R，记 $g (x) = f^{'} (x) .$ 若 $f (\frac{3}{2} - 2 x) ，$ $g (2 + x)$ 均为偶函数，则（）

A、 $f (0) = 0$ B、 $g (- \frac{1}{2}) = 0$ C、 $f (- 1) = f (4)$ D、 $g (- 1) = g (2)$

查看试题解析

三、填空题

10. 若曲线 $y = (x + a) e^{x}$ 有两条过坐标原点的切线，则a的取值范围是.

查看试题解析
11. 曲线 $y = \frac{2 x - 1}{x + 2}$ 在点（-1，-3）处的切线方程为。

查看试题解析
12. 设函数 $f (x) = \frac{e^{x}}{x + a}$ ．若 $f^{'} (1) = \frac{e}{4}$ ，则a= ．

查看试题解析
13. 曲线y=3(x²+x)e^x在点(0，0)处的切线方程为.

查看试题解析

四、解答题

14. 已知函数 $f (x) = \frac{3 - 2 x}{x^{2} + a}$ ．

(1)、若 $a = 0$ ，求 $y = f (x)$ 在 $(1 ， f (1))$ 处切线方程；

(2)、若函数 $f (x)$ 在 $x = - 1$ 处取得极值，求 $f (x)$ 的单调区间，以及最大值和最小值．

查看试题解析
15. 某地准备在山谷中建一座桥梁，桥址位置的竖直截面图如图所示：谷底O在水平线MN上、桥AB与MN平行， $O O^{'}$ 为铅垂线( $O^{'}$ 在AB上).经测量，左侧曲线AO上任一点D到MN的距离 $h_{1}$ (米)与D到 $O O^{'}$ 的距离a(米)之间满足关系式 $h_{1} = \frac{1}{40} a^{2}$ ；右侧曲线BO上任一点F到MN的距离 $h_{2}$ (米)与F到 $O O^{'}$ 的距离b(米)之间满足关系式 $h_{2} = - \frac{1}{800} b^{3} + 6 b$ .已知点B到 $O O^{'}$ 的距离为40米.

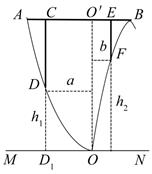(1)、求桥AB的长度；

(2)、计划在谷底两侧建造平行于 $O O^{'}$ 的桥墩CD和EF，且CE为80米，其中C，E在AB上(不包括端点).桥墩EF每米造价k(万元)、桥墩CD每米造价 $\frac{3}{2} k$ (万元)(k>0).问 $O^{'} E$ 为多少米时，桥墩CD与EF的总造价最低?

查看试题解析
16. 已知函数 $f (x) = 12 - x^{2}$ ．
（Ⅰ）求曲线 $y = f (x)$ 的斜率等于 $- 2$ 的切线方程；

（Ⅱ）设曲线 $y = f (x)$ 在点 $(t ， f (t))$ 处的切线与坐标轴围成的三角形的面积为 $S (t)$ ，求 $S (t)$ 的最小值．

查看试题解析
17. 设函数 $f (x) = (x - a) (x - b) (x - c), a, b, c \in R$ 、 $f' (x)$ 为f（x）的导函数．

(1)、若a=b=c ， f（4）=8，求a的值；

(2)、若a≠b ， b=c ，且f（x）和 $f' (x)$ 的零点均在集合 ${- 3, 1, 3}$ 中，求f（x）的极小值；

(3)、若 $a = 0, 0 < b ⩽ 1, c = 1$ ，且f（x）的极大值为M ，求证:M≤ $\frac{4}{27}$ ．

查看试题解析
18. 已知函数 $f (x) = e^{x} - a x$ 和 $g (x) = a x - ln x$ 有相同的最小值.

(1)、求a；

(2)、证明：存在直线 $y = b ，$ ，其与两条曲线 $y = f (x)$ 和 $y = g (x)$ 共有三个不同的交点，并且从左到右的三个交点的横坐标成等差数列．

查看试题解析
19. 已知函数 $f (x) = (x - 1) e^{x} - a x^{2} + b$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、从下面两个条件中选一个，证明： $f (x)$ 有一个零点
① $\frac{1}{2} < a \leq \frac{e^{2}}{2} ， b > 2 a$ ；

② $0 < a < \frac{1}{2} ， b \leq 2 a$ ．

查看试题解析
20. 设a ， b为实数，且 $a > 1$ ，函数 $f (x) = a^{x} - b x + e^{2} (x \in R)$
(注： $e = 2.71828 \cdot \cdot \cdot$ 是自然对数的底数)

(1)、求函数 $f (x)$ 的单调区间；

(2)、若对任意 $b > 2 e^{2}$ ，函数 $f (x)$ 有两个不同的零点，求a的取值范围；

(3)、当 $a = e$ 时，证明：对任意 $b > e^{4}$ ，函数 $f (x)$ 有两个不同的零点 $x_{1} ， x_{2}$ ，满足 $x_{2} > \frac{b \ln b}{2 e^{2}} x_{1} + \frac{e^{2}}{b}$ .

查看试题解析
21. 已知函数 $f (x) = x^{3} - x^{2} + a x + 1$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、求曲线 $y = f (x)$ 过坐标原点的切线与曲线 $y = f (x)$ 的公共点的坐标.

查看试题解析
22. 设函数 $f (x) ＝ a^{2} x^{2} ＋ a x - 3 ln x ＋ 1$ ，其中a>0．

(1)、讨论f(x)的单调性；

(2)、若y＝f(x)的图像与x轴没有公共点，求a的取值范围．

查看试题解析
23. 已知a＞0且a≠1，函数f（x）= $\frac{x^{a}}{a^{x}}$ （x＞0），

(1)、当a=2时，求f（x）的单调区间；

(2)、若曲线y= f（x）与直线y=1有且仅有两个交点，求a的取值范围.

查看试题解析
24. 设函数f（x）=ln（a-x），已知x=0是函数y=xf（x）的极值点。

(1)、求a；

(2)、设函数g（x）= $\frac{x + f （ x ）}{x f （ x ）}$ ，证明：g（x）＜1.

查看试题解析