2019-2023高考数学真题分类汇编9 三角函数及解三角形(3)
试卷更新日期:2023-09-01 类型:二轮复习
一、单选题
-
1. 若α为第四象限角,则( )A、cos2α>0 B、cos2α<0 C、sin2α>0 D、sin2α<02. 已知 ,且 ,则 ( )A、 B、 C、 D、3. 设函数 在 的图像大致如下图,则f(x)的最小正周期为( )
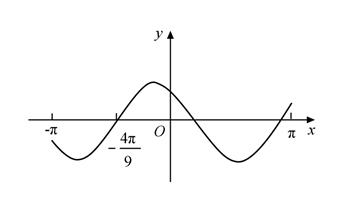 A、 B、 C、 D、4. 已知函数 .给出下列结论:
A、 B、 C、 D、4. 已知函数 .给出下列结论:① 的最小正周期为 ;② 是 的最大值;③把函数 的图象上所有点向左平移 个单位长度,可得到函数 的图象.其中所有正确结论的序号是( )
A、① B、①③ C、②③ D、①②③5. 已知 ,则“存在 使得 ”是“ ”的( ).A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件6. 已知函数 是奇函数,且 的最小正周期为 ,将 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为 .若 ,则 ( )A、-2 B、- C、 D、27. 已知函数 是奇函数,将 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,且 ,则 ( )A、 B、 C、 D、8. 设函数f(x)=sin(ωx+ )(ω>0),已如f(x)在[0,2π]有且仅有5个零点,下述四个结论:①f(x)在(0,2π)有且仅有3个极大值点②f(x)在(0,2π)有且仅有2个极小值点③f(x)在(0, )单调递增④ω的取值范围[ , )其中所有正确结论的编号是( )A、①④ B、②③ C、①②③ D、①③④9. 若 , 是函数f(x)= sinωx(ω>0) 两个相邻的极值点,则ω( )A、2 B、 C、1 D、10. 下列函数中,以 为周期且在区间( , )单调递增的是( )A、f(x)=│cos2x│ B、f(x)=│sin 2x│ C、f(x)=cos│x│ D、f(x)= sin│x│11. 已知α∈(0, ),2sin2α=cos2α+1,则sinα=( )A、 B、 C、 D、12. 如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β.图中阴影区域的面积的最大值为( )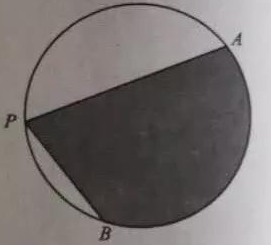 A、4β+4cosβ B、4β+4sinβ C、2β+2cosβ D、2β+2sinβ13. cos2 -sin2 =( )A、 B、 C、 D、
A、4β+4cosβ B、4β+4sinβ C、2β+2cosβ D、2β+2sinβ13. cos2 -sin2 =( )A、 B、 C、 D、二、多选题
-
14. 已知O为坐标原点,点P1(cosα,sinα),P2(cosβ,-sinβ),P3(cos(α+β),sin(α+β)),A(1,0),则( )A、| = B、 = C、 = D、15. 下图是函数y= sin(ωx+φ)的部分图像,则sin(ωx+φ)= ( )
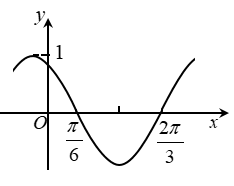
A、 B、 C、 D、三、填空题
-
16. 某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O为圆孔及轮廓圆弧AB所在圆的圆心,A是圆弧AB与直线AG的切点,B是圆弧AB与直线BC的切点,四边形DEFG为矩形,BC⊥DG,垂足为C,tan∠ODC= , ,EF=12 cm,DE=2 cm,A到直线DE和EF的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为cm2 .
 17. 将函数y= 的图象向右平移 个单位长度,则平移后的图象中与y轴最近的对称轴的方程是.18. 若函数 的最大值为2,则常数 的一个取值为 .19. 已知 ,则 的值是.20. 函数f(x)=sin22x的最小正周期是.21. 函数f(x)=sin(2x+ )-3cosx的最小值为.
17. 将函数y= 的图象向右平移 个单位长度,则平移后的图象中与y轴最近的对称轴的方程是.18. 若函数 的最大值为2,则常数 的一个取值为 .19. 已知 ,则 的值是.20. 函数f(x)=sin22x的最小正周期是.21. 函数f(x)=sin(2x+ )-3cosx的最小值为.
四、解答题
-
22. 设函数f(x)=sinx,x R。(1)、已知θ∈[0,2π),函数f(x+θ)是偶函数,求θ的值(2)、求函数y=[f(x+) ]2+[f(x+ )]2的值域23. 在 中,内角 所对的边分别为 .已知 , .
(Ⅰ)求 的值;
(Ⅱ)求 的值.
24. 在△ABC中,a=3,b-c=2,cosB=- .(I)求b,c的值:
(II)求sin(B+C)的值.