2019-2023高考数学真题分类汇编8 指数型、对数型、幂函数型函数及抽象函数
试卷更新日期:2023-09-01 类型:二轮复习
一、选择题
-
1. 已知 ,则 ( )A、25 B、5 C、 D、2. 已知 ,则下列判断正确的是( )A、 B、 C、 D、3. 青少年视力是社会普遍关注的问题,视力情况可借助视力表测量,通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记数法的数据V满足L=5+lgV。已知某同学视力的五分记录法的数据为4.9,则其视力的小数记数法的数据约为( )( ≈1.259)A、1.5 B、1.2 C、0.8 D、0.64. 设 ,则a , b , c的大小关系为( )A、 B、 C、 D、5. 设 ,则 ( )A、 B、 C、 D、6. 函数f(x)=loga(4-x)(a>0,且a≠1)的定义域是( )A、(0,4) B、(4,+∞) C、(-∞,4) D、(-∞,4)∪(4,+∞)7. 若 , 则的大小关系为( )A、 B、 C、 D、8. 化简的值为( )A、1 B、2 C、4 D、69. 已知 , , , 则( )A、 B、 C、 D、10. 函数 在区间 的图像大致为( )A、

B、
B、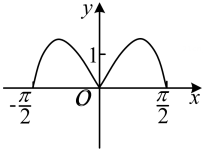
C、
C、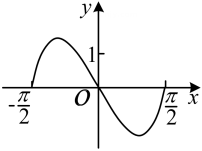
D、
D、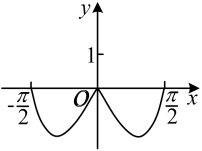
11. 已知函数 的定义域均为R,且 .若 的图像关于直线 对称, ,则 ( )A、-21 B、-22 C、-23 D、-2412. 已知函数 ,则对任意实数 ,有( )A、 B、 C、 D、13. 设 , , ,则( )A、a<b<c B、b<c<a C、b<a<c D、c<a<b14. 设a=log32,b=log53,c= ,则( )A、a<c<b B、a<b<c C、b<c<a D、c<a<b15. 已知55<84 , 134<85 . 设a=log53,b=log85,c=log138,则( )A、a<b<c B、b<a<c C、b<c<a D、c<a<b16. 若 ,则( )A、 B、 C、 D、17. 已知 ,则 的大小关系为( )A、 B、 C、 D、18. 已知函数 若关于 的方程 恰有两个互异的实数解,则 a 的取值范围为( )A、 B、 C、 D、19. 已知 , , ,则 的大小关系为( )A、 B、 C、 D、20. 2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日 点的轨道运行. 点是平衡点,位于地月连线的延长线上.设地球质量为M1 , 月球质量为M2 , 地月距离为R, 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
11. 已知函数 的定义域均为R,且 .若 的图像关于直线 对称, ,则 ( )A、-21 B、-22 C、-23 D、-2412. 已知函数 ,则对任意实数 ,有( )A、 B、 C、 D、13. 设 , , ,则( )A、a<b<c B、b<c<a C、b<a<c D、c<a<b14. 设a=log32,b=log53,c= ,则( )A、a<c<b B、a<b<c C、b<c<a D、c<a<b15. 已知55<84 , 134<85 . 设a=log53,b=log85,c=log138,则( )A、a<b<c B、b<a<c C、b<c<a D、c<a<b16. 若 ,则( )A、 B、 C、 D、17. 已知 ,则 的大小关系为( )A、 B、 C、 D、18. 已知函数 若关于 的方程 恰有两个互异的实数解,则 a 的取值范围为( )A、 B、 C、 D、19. 已知 , , ,则 的大小关系为( )A、 B、 C、 D、20. 2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日 点的轨道运行. 点是平衡点,位于地月连线的延长线上.设地球质量为M1 , 月球质量为M2 , 地月距离为R, 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:.设 ,由于 的值很小,因此在近似计算中 ,则r的近似值为( )
A、 B、 C、 D、21. 若a>b,则( )A、ln(a−b)>0 B、3a<3b C、a3−b3>0 D、│a│>│b│22. 在天文学中,天体的明暗程度可以用星等或亮度来描述。两颗星的星等与亮度满足m2-m1= ,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是-26.7,天狼星的星等是-1.45,则太阳与天狼星的亮度的比值为( )A、1010.1 B、10.1 C、lg10.1 D、10-10.123. 已知 ,则( )A、 B、 C、 D、24. 设函数 的定义域为R , 满足 ,且当 时, .若对任意 ,都有 ,则m的取值范围是( )A、 B、 C、 D、二、填空题
-
25. 已知函数 , 则 .26. 写出一个同时具有下列性质①②③的函数 .
① ;②当 时, ;③ 是奇函数.
27. 如图是一个算法流程图,若输出y的值为-2,则输入x的值是.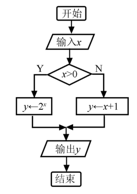 28. 函数 的反函数为 .
28. 函数 的反函数为 .
29. 已知 , 则的值域是 ;30. 已知函数 则 ;若当 时, ,则 的最大值是 .31. 设函数 ,若 存在最小值,则 的一个取值为; 的最大值为 .32. 已知函数 ,函数 的图象在点 和点 的两条切线互相垂直,且分别交y轴于M,N两点,则 取值范围是 .三、解答题
-
33. 改革开放40年,我国卫生事业取得巨大成就,卫生总费用增长了数十倍.卫生总费用包括个人现在支出、社会支出、政府支出,如表为2012年
 年我国卫生货用中个人现金支出、社会支出和政府支出的费用(单位:亿元)和在卫生总费用中的占比.
年我国卫生货用中个人现金支出、社会支出和政府支出的费用(单位:亿元)和在卫生总费用中的占比.年份
卫生总费用(亿元)
个人现金卫生支出
社会卫生支出
政府卫生支出
绝对数(亿元)
占卫生总费用比重
绝对数(亿元)
占卫生总费用比重
绝对数(亿元)
占卫生总费用比重
2012
28119.00
9656.32
34.34
10030.70
35.67
8431.98
29.99
2013
31668.95
10729.34
33.88
11393.79
35.98
9545.81
30.14
2014
35312.40
11295.41
31.99
13437.75
38.05
10579.23
29.96
2015
40974.64
11992.65
29.27
16506.71
40.29
12475.28
30.45
(数据来源于国家统计年鉴)
(1)、指出2012年到2015年之间我国卫生总费用中个人现金支出占比和社会支出占比的变化趋势:(2)、设 表示1978年,第 年卫生总费用与年份 之间拟合函数 研究函数 的单调性,并预测我国卫生总费用首次超过12万亿的年份.