黑龙江省哈尔滨市道里区2022-2023学年七年级下学期期末数学试卷(五四学制)
试卷更新日期:2023-09-01 类型:期末考试
一、选择题。(每题3分,共30分)
-
1. 二元一次方程x+y=2023( )A、只有一个解 B、只有两个解 C、无数个解 D、无解2. 下列长度的三条线段能组成三角形的是( )A、2,3,6 B、4,5,9 C、2,2,5 D、3,4,53. 在如图中,正确画出△ABC的边BC上的高的是( )A、
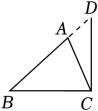 B、
B、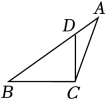 C、
C、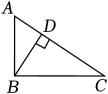 D、
D、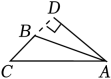 4. 已知a<b,下面四个不等式中不正确的是( )A、3a<3b B、a+3<b+3 C、-3a<-3b D、a-3<b-35. 在统计中,样本的方差可以近似地反映总体的( )A、最大值与最小值 B、平均状态 C、分布规律 D、波动大小6. 一个多边形的每个内角都相等,这个多边形的外角不可能是( )A、30° B、40° C、50° D、60°7. 如图,将△ACD沿AD翻折,点C落在AB上的点C′处,若∠BC′D=120°,∠B=40°,则∠DAC为( )
4. 已知a<b,下面四个不等式中不正确的是( )A、3a<3b B、a+3<b+3 C、-3a<-3b D、a-3<b-35. 在统计中,样本的方差可以近似地反映总体的( )A、最大值与最小值 B、平均状态 C、分布规律 D、波动大小6. 一个多边形的每个内角都相等,这个多边形的外角不可能是( )A、30° B、40° C、50° D、60°7. 如图,将△ACD沿AD翻折,点C落在AB上的点C′处,若∠BC′D=120°,∠B=40°,则∠DAC为( ) A、80° B、60° C、50° D、40°8. 在平面直角坐标系中,(2-m,m-3)在第二象限,则m的取值范围是(( )A、m>2 B、m>3 C、m<2 D、2<m<39. 足球比赛的得分规则如下:胜一场得3分,平一场得1分,负一场得0分.某足球队一共进行了14场比赛,其中负了5场,共得19分.设该球队胜了x场,平了y场,依题意可列方程组( )A、 B、 C、 D、10. m,n为实数,若关于x、y的方程组 无解,则关于a的不等式ma>的解集是( )A、a>- B、a>-3 C、a<- D、a<-3
A、80° B、60° C、50° D、40°8. 在平面直角坐标系中,(2-m,m-3)在第二象限,则m的取值范围是(( )A、m>2 B、m>3 C、m<2 D、2<m<39. 足球比赛的得分规则如下:胜一场得3分,平一场得1分,负一场得0分.某足球队一共进行了14场比赛,其中负了5场,共得19分.设该球队胜了x场,平了y场,依题意可列方程组( )A、 B、 C、 D、10. m,n为实数,若关于x、y的方程组 无解,则关于a的不等式ma>的解集是( )A、a>- B、a>-3 C、a<- D、a<-3二、填空题。(每题3分,共24分)
-
11. 如图,工程建筑中的屋顶钢架经常采用三角形的结构,其中的数学道理是 .
 12. 如果|x-3|=3-x,则x的范围是 .13. 已知x=1,y=-2是方程3mx-2y=7的解,则m的值为 .14. 如果一个多边形的内角和是外角和的2倍,则这个多边形是边形.15. 不等式组的解集是x>3,那么α的取值范围是 .16. 如图,△ABC的两条中线BE,CF交于点O,若三角形△ABC的面积为12,则四边形AFOE的面积是 .
12. 如果|x-3|=3-x,则x的范围是 .13. 已知x=1,y=-2是方程3mx-2y=7的解,则m的值为 .14. 如果一个多边形的内角和是外角和的2倍,则这个多边形是边形.15. 不等式组的解集是x>3,那么α的取值范围是 .16. 如图,△ABC的两条中线BE,CF交于点O,若三角形△ABC的面积为12,则四边形AFOE的面积是 . 17. 在一次中学生田径运动会上,参加男子跳高的20名运动员的成绩如表所示:
17. 在一次中学生田径运动会上,参加男子跳高的20名运动员的成绩如表所示:成绩(单位:米)
1.54
1.63
1.68
1.74
1.75
1.82
1.85
1.92
人数
3
5
2
2
4
2
1
1
这些运动员成绩的中位数为 .
18. △ABC的角平分线BD与角平分线CE交于点F,连接AF,若∠FBC=25°,FE=FD,则∠FAD为 度.三、解答题。(66分)
-
19. 解不等式:(1)、5x+10>3x-2;(2)、-1.20. 解方程组:(1)、;(2)、21. 如图,ABCDE为正五边形.
 (1)、求∠A的度数;(2)、连接BD,CE,求证:BD=CE.22. 某班50名同学进行科普知识竞赛,根据50名同学的成绩绘成如图所示的统计图.
(1)、求∠A的度数;(2)、连接BD,CE,求证:BD=CE.22. 某班50名同学进行科普知识竞赛,根据50名同学的成绩绘成如图所示的统计图. (1)、这50名同学竞赛成绩的众数为多少(直接写答案,不必说明理由)?(2)、求这50名同学的平均成绩?(3)、甲同学在竞赛前练习的5次成绩分别为: 60 ,60,90,70,70(单位:分),求这5个数据的方差.23. x取哪些整数值时,不等式5x-2>3(x-1)与都成立?24. 四边形ABCD,AD⊥CD,点E在CD上,点F在AE上,连接CF,∠FCE+3∠DAE=∠D.
(1)、这50名同学竞赛成绩的众数为多少(直接写答案,不必说明理由)?(2)、求这50名同学的平均成绩?(3)、甲同学在竞赛前练习的5次成绩分别为: 60 ,60,90,70,70(单位:分),求这5个数据的方差.23. x取哪些整数值时,不等式5x-2>3(x-1)与都成立?24. 四边形ABCD,AD⊥CD,点E在CD上,点F在AE上,连接CF,∠FCE+3∠DAE=∠D. (1)、如图1,求证:∠CFE=2∠DAE;(2)、如图2,点G在AE上,连接BG,BG=CF,∠ABG=2∠DAE,∠BAD-∠CFE=90°,求证:AG=EC;(3)、如图3,在(2)的条件下,过点G作CD的平行线交AD于点H,CE=2DE,AF=6,求HG的值.25. 在平面直角坐标系中,点O为坐标原点,点A在x轴上,点B在y轴上,点B的纵坐标为b,实数a、b满足方程组 .
(1)、如图1,求证:∠CFE=2∠DAE;(2)、如图2,点G在AE上,连接BG,BG=CF,∠ABG=2∠DAE,∠BAD-∠CFE=90°,求证:AG=EC;(3)、如图3,在(2)的条件下,过点G作CD的平行线交AD于点H,CE=2DE,AF=6,求HG的值.25. 在平面直角坐标系中,点O为坐标原点,点A在x轴上,点B在y轴上,点B的纵坐标为b,实数a、b满足方程组 . (1)、求a,b的值;(2)、如图1,过点O作AB的垂线,点C为垂足,线段OP的长为t,△OPC的面积为S(S≠0),用含t的式子表示S,不要求写出t的范围;(3)、在(2)的条件下,如图2,点D在第二象限,∠ODB=90°,连接DP,DP∥AO,S= , 求OD的长.
(1)、求a,b的值;(2)、如图1,过点O作AB的垂线,点C为垂足,线段OP的长为t,△OPC的面积为S(S≠0),用含t的式子表示S,不要求写出t的范围;(3)、在(2)的条件下,如图2,点D在第二象限,∠ODB=90°,连接DP,DP∥AO,S= , 求OD的长.