辽宁省葫芦岛市绥中县2022-2023学年七年级下册数学期末试卷
试卷更新日期：2023-09-01 类型：期末考试
一、选择题：(本大题共10个小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项是符合题目要求的.请将符合要求的答案的序号涂在答题卡上)
-
1. 下列说法正确的是（ ），A、|-2|=-2 B、0的倒数是0 C、4的平方根是2 D、-的相反数是2. 若a<b，则下列变形错误的是（ ）.A、a-2<b-2 B、2a+1<2b+1 C、-2a<-2b D、3. 已知(4-a)²与互为相反数，则a-b的平方根是（ ）、A、 B、 C、± D、±4. 二元一次方程组的解为 ， 则被遮盖的前后两个数分别为（ ）.A、1、2 B、1、5 C、5、1 D、2、45. 在平面直角坐标系中，点P(m+1，2-m)在第二象限，则m的取值范围为（ ）.A、m<-1 B、m<2 C、m>2 D、-1<m<26. 某学校为了了解学生对“禁止学生带手机进入校园”这一规定的意见，随机抽取100名学生进行调查，这一问题中的样本是（ ）.A、100 B、被抽取的100名学生的意见 C、被抽取的100名学生 D、全校学生的意见7. 下列命题中，是真命题的是（ ）A、若两个角的和为180°，则这两个角为邻补角 B、相等的角是对顶角 C、同旁内角相加为180° D、平面内，垂直于同一条直线的两条直线互相平行8. 在平面直角坐标系中，将点M(a+1，3-a)向右平移1个单位长度得到点N，若点N在y轴上，则点M的坐标为（ ）.A、(1，5) B、(-1，5) C、(-1，3) D、(1，3)9. 如图，小明观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：已知AB//CD，∠BAE=91°，∠DCE=124°，则∠AEC的度数是（ ）
A、29° B、30° C、31° D、33°10. 如图，将一副三角板的直角顶点重合放置，得到下列结论，其中正确的有（ ），
①∠2=∠3；
②如果∠3=60°，那么AC//DE；
③如果BC//AD，那么∠2=45°
④如果∠CAD=150°，那么∠4=∠C.
A、1个 B、2个 C、3个 D、4个二、填空题(每小题3分，共24分)
-
11. 的立方根是；2-的绝对值是12. 语句“x的4倍与3的和不大于6”用不等式表示为13. 若线段AB//x轴，且A(2，m)，B(3，1)，则m的值为14. 一件衬衫进价50元，问定价至少是多少元，打八折后才不会亏本?设定价为x元，则根据题意可列不等式为15. 给出下面一组数据：19，20，25，31，28，27，26，21，20，22，24，23，25，29，27，28，27，30，18，20.若组距为2，则这组数据应分成组。16. 如图，AB、CD相交于点O，OM平分∠BOD，∠MON是直角，∠AOC=50°，则∠DON的度数是.
17. 若x²a-3b+2y5a+b-10=0是二元一次方程，那么a、b的值分别是.18. 下列说法中：①座位是4排2号；②某城市在东经118°，北纬29°；③某校在文化路229号；④甲地距乙地3km.其中能确定位置的有.(填序号即可)三、简答题：(共66分)
-
19. 计算20. 解方程组：21. 解不等式组把解集在数轴上表示出来.并写出其整数解
22. 用方程组解决问题：某校初一(1)班30名同学为“希望工程”捐款，共捐款300元，捐款情况如下表：
捐款/元 2 5 10 15 人数 5 
10 表格中捐款5元和10元的人数被墨水污染了，问：捐5元和10元的人数各是多少?
23. 已知：如图，在△ABC中，BD⊥AC于点D，E为BC上一点，过E点作EF⊥AC，垂足为F，过D作DH//BC交AB于点H.
(1)、请你补全图形(2)、求证：∠BDH=∠CEF.24. 为了创设全新的校园文化氛围，进一步组织学生开展课外阅读，让学生在丰富多彩的书海中，扩大知识源，亲近母语，提高文学素养．某校准备开展“与经典为友、与名著为伴”的阅读活动，活动前对本校学生进行了“你最喜欢的图书类型 只写一项 ”的随机抽样调查，相关数据统计如图：
请根据以上信息解答下列问题：
(1)、该校对多少名学生进行了抽样调查？(2)、请将图1和图2补充完整；并求出扇形统计图中小说所对应的圆心角度数．(3)、已知该校共有学生700人，利用样本数据估计全校学生中最喜欢小说人数约为多少人？25. 已知：A(0，1)，B(2，0)，C(4，3)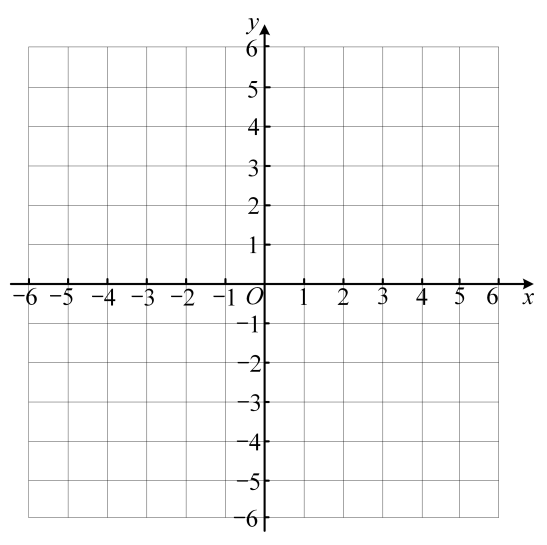
⑴在坐标系中描出各点，画出△ABC.
⑵将△ABC向右平移2个单位长度，再向下平移1个单位长度，得到△A'B'C'，请画出平移后的图形△A'B'C'.
⑶求△ABC的面积；
⑷设点P在X轴上，且△ABP与△ABC的面积相等，求点P的坐标.
26.
(1)、如图1，已知AB//CD，∠AEP=40°，∠PFD=110°，求∠EPF的度数.(2)、如图2，AB//CD，点P在AB的上方，问∠PEA，∠PFC，∠BPP之间有何数量关系?并说明理由；(3)、如图3，在(2)的条件下，已知，∠EPF=60°，∠PEA的平分线和∠PFC的平分线交点G，求∠G的度数.