云南省昆明市昆八中2023-2024学年高二上学期数学特色部开学考试试卷
试卷更新日期:2023-09-01 类型:开学考试
一、单选题(本大题共8小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
-
1. 已知角的终边经过点 , 则( )A、 B、 C、 D、2. 下列各组函数是同一函数的是( )A、与 B、与 C、 D、与3. 下列函数中不能用二分法求零点近似值的是( )A、 B、 C、 D、4. 如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是( )
 A、棱柱 B、棱台 C、棱柱与棱锥的组合体 D、不能确定5. 某工厂近期唕生产一批化工试剂,经市场调查得知,生产这批试剂的成本分为以下三个部分: ①生产1单位试剂需要原料费50元;②支付所有职工的工资总额由7500元的基本工资和每生产1单位试剂补贴20元组成;③后续保养的费用是每单位元(试剂的总产量为单位,),则要使生产每单位试剂的成本最低,试剂总产量应为( )A、60单位 B、70单位 C、80单位 D、90单位6. 某学校随机抽取了部分学生,对他们每周使用手机的时间进行统计,得到如下的频率分布直方图.则下列说法:①;②若抽取100人,则平均用时13.75小时:③若从每周使用时间在 , 三组内的学生中用分层抽样的方法选取8人进行访谈,则应从使用时间在内的学生中选取的人数为3.其中正确的序号是( )
A、棱柱 B、棱台 C、棱柱与棱锥的组合体 D、不能确定5. 某工厂近期唕生产一批化工试剂,经市场调查得知,生产这批试剂的成本分为以下三个部分: ①生产1单位试剂需要原料费50元;②支付所有职工的工资总额由7500元的基本工资和每生产1单位试剂补贴20元组成;③后续保养的费用是每单位元(试剂的总产量为单位,),则要使生产每单位试剂的成本最低,试剂总产量应为( )A、60单位 B、70单位 C、80单位 D、90单位6. 某学校随机抽取了部分学生,对他们每周使用手机的时间进行统计,得到如下的频率分布直方图.则下列说法:①;②若抽取100人,则平均用时13.75小时:③若从每周使用时间在 , 三组内的学生中用分层抽样的方法选取8人进行访谈,则应从使用时间在内的学生中选取的人数为3.其中正确的序号是( ) A、①② B、①③ C、②③ D、①②③7. 已知事件与事件是互斥事件,则( )A、 B、 C、 D、8. 21世纪以来,中国钢铁工业进入快速发展阶段,某工厂要加工一种如图所示的圆锥体容器,圆锥的高和母线长分别为和 , 该容器需要在圆锥内部挖出一个正方体槽,则可以挖出的正方体的最大棱长为( )
A、①② B、①③ C、②③ D、①②③7. 已知事件与事件是互斥事件,则( )A、 B、 C、 D、8. 21世纪以来,中国钢铁工业进入快速发展阶段,某工厂要加工一种如图所示的圆锥体容器,圆锥的高和母线长分别为和 , 该容器需要在圆锥内部挖出一个正方体槽,则可以挖出的正方体的最大棱长为( )
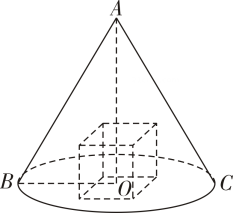 A、 B、 C、 D、
A、 B、 C、 D、二、多选题(本大题共4小题,每小题5分,在每小题给出的四个选项中,有多项是符合题目要求的.)
-
9. 下列运算中正确的是( )A、 B、 C、当时, D、若 , 则10. 将函数的图象向右来移个单位长度,再将图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到的图象,则( )A、 B、在上单调递减 C、直线是图象的一条对称轴 D、在上的最小值为-211. 已知函数是上的减函数,则实数的可能的取值有( )A、4 B、5 C、6 D、712. 已知 , 点满足且 , 则( )A、 B、 C、 D、
三、填空题(本大题共4小题,每小题5分。)
-
13. 若指数函数的图象经过点 , 则;不等式的解集是.14. 市场上有甲、乙、丙三家工厂生产的同一品牌产品,已知三家工厂的市场占有率分别为 , , 且三家工厂的次品率分别为 , 则市场上该品牌产品的次品率为.15. 在中,角A,B,C所对的边分别为a,b,c,且.若 , 则面积的最大值为;若 , 则.16. 正方体的棱长为2,点为底面正方形ABCD的中心,点在侧面正方形的边界及其内部运动,若 , 则点的轨迹的长度为.
四、解答题(本大题共70分,解答应写出文字说明,证明过程或演算步骤。)
-
17. 在平面直角坐标系xOy中,角的始边为轴的非负半轴,终边经过点 , 求下列各式的值:(1)、;(2)、.18. 从某小区抽取100户居民用户进行月用电量调查,发现他们的用电量都在50~350(单位:)之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示:
 (1)、求在被调查的用户中,用电量落在区间的户数;(2)、求直方图中的值;(3)、求这组数据的平均数.19. 如图,直三棱柱中,点是BC上一点.
(1)、求在被调查的用户中,用电量落在区间的户数;(2)、求直方图中的值;(3)、求这组数据的平均数.19. 如图,直三棱柱中,点是BC上一点. (1)、若点D是BC的中点.求证;(2)、若平面⊥平面 , 求证.20. 在①;②③这三个条件中选一个,补充在下面问题中,并加以解答.
(1)、若点D是BC的中点.求证;(2)、若平面⊥平面 , 求证.20. 在①;②③这三个条件中选一个,补充在下面问题中,并加以解答.问题:在中,角A,B,C所对的边分别为a,b,c,已知 , 解三角形.
21. 设为实数,已知函数是奇函数.(1)、求的值;(2)、证明:在区间上单调递减:(3)、当时,求函数的取值范围.22. A地某校准备组织学生及学生家长到B地进行社会实践,为便于管理,所有人员必须乘坐在同一列火车上.根据报名人数,若都买一等座单程火车票需17010元,若都买二等座单程火车票且花钱最少,则需11220元.已知学生家长与教师的人数之比为2:1,从A到B的火车票价格(部分)如下表所示:运行区间
公布票价
学生票
上车站
下车站
一等座
二等座
二等座
A
B
81(元)
68(元)
51(元)
(1)、参加社会实践的老师、家长与学生各有多少人?(2)、由于各种原因,二等座火车票只能买x张(x小于参加社会实践的人数),其余的需买一等座火车票,在保证每位参与人员都有座位的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.(3)、请你做一个预算,按第⑵小题中的购票方案,购买单程火车票至少要花多少钱﹖最多要花多少钱?