辽宁省阜新市海州区2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、选择题（在每一小题给出的四个选项中，只有一个是正确的．每小题3分，共30分）

1. 下列冬奥元素图片中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 计算 $a \cdot a^{2}$ 的正确结果是（）

A、 $2 a^{2}$ B、 $3 a$ C、 $a^{2}$ D、 $a^{3}$

查看试题解析
3. 下列图形中，∠1和∠2为同旁内角的是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、 $2 a^{2} + a^{3} = 3 a^{5}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $2 a^{3} \div a = 2 a$ D、 ${(2 a)}^{3} = 8 a^{3}$

查看试题解析
5. 下列事件中，是必然事件的是（）

A、掷一次骰子，向上的一面的点数是1 B、13位学生参加一个聚会，他们中至少有两位学生的生日在同一个月（可以不同年） C、经过有交通信号灯的路口，遇到红灯 D、射击运动员射击一次，命中靶心

查看试题解析
6. 如图，AD是△ABC的高，BE是△ABC的角平分线，∠BAD＝40°，∠BEC＝80°，则∠DAC的大小是（）；

A、30° B、25° C、15° D、20°

查看试题解析
7. 如图，AB＝AC ， AD＝AE ， ∠BAC＝∠DAE ，点B ， D ， E在同一直线上，若∠1＝25°，∠2＝35°，则∠3的度数是（）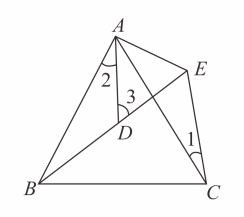

A、50° B、55° C、60° D、70°

查看试题解析
8. 如表列出了一项实验的统计数据（单位：cm）：

x

30

45

55

80

…

y

50

80

100

150

…

它表示皮球从一定高度落下时，下落高度y与弹跳高度x的关系，那么变量y与x之间的关系式能表示为（）

A、y＝2x－10 B、y＝x² C、y＝x＋25 D、y＝x＋5

查看试题解析
9. 如图，在Rt△ABC中，∠C＝90°，首先以顶点B为圆心，任意长度为半径作弧，在边BC、BA上截取BE、BD；然后分别以点D、E为圆心，大于 $\frac{1}{2} D E$ 为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G ．若CG＝4，P为边AB上一动点，则GP的最小值为（）

A、2 B、8 C、4 D、无法确定

查看试题解析
10. 如图，点M是线段AB的中点，点P在MB上，分别以AP、PB为边，在线段AB同侧作正方形APCD和正方形PBEF ，连接MD和ME ，设AP＝m、BP＝n ，且m＋n＝6，mn＝7，则图中阴影部分的面积为（）

A、24.5 B、13 C、18 D、21

查看试题解析

二、填空题（每小题3分，共18分）

11. 可乐和奶茶含有大量的咖啡因，世界卫生组织建议青少年每天摄入的咖啡因不能超过0.000085kg，将数据0.000085用科学记数法表示为.

查看试题解析
12. “学习强国”的英语“Learningpower”中，字母“n”出现的频率为．

查看试题解析
13. 如图，把一块含30°角的三角尺的直角顶点放在直尺的一边上，如果∠1＝37°，那么∠2的度数为°．

查看试题解析
14. 在数学拓展课《折叠的奥秘》中，老师提出一个问题：如图，有一条长方形纸带ABCD ，点E在AD上，点F在BC上，把长方形纸带沿EF折叠，若 $∠ B^{'} F B = 80 °$ ，则∠AEF＝．

查看试题解析
15. 如图，在△ABC中，AB的垂直平分线交AC于点D ，交AB于点E ．若AE＝5，△CBD的周长为18，则△ABC的周长为．

查看试题解析
16. 如图，AB＝18m，CA⊥AB于A，DB⊥AB于B，且AC＝6m，点P从B向A运动，每秒钟走1m，Q点从B向D运动，每秒钟走2m，点P，Q同时出发，运动秒后，△CAP与△PQB全等．

查看试题解析

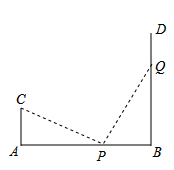
三、解答题（17题12分，18、19题每题8分，20、21题每题10分，22、23题每题12分，共72分）

17. 计算：

(1)、 ${(- \frac{1}{2})}^{- 1} + {(- 2)}^{2} + {(π - 3.14)}^{0}$ ；

(2)、 $a^{3} \cdot a^{5} + {(a 2)}^{4} + {(- 3 a^{4})}^{2}$ ；

(3)、 $(4 x^{3} y - 6 x^{2} y^{2} + 2 x y) \div (- 2 x y)$ ．

查看试题解析
18. 先化简，再求值：

(1)、（x＋2）（x－3）＋x（x－3），其中x＝2：

(2)、（2x－1）²＋（x＋2）（x－2）－4x（x－1），其中x＝－2．

查看试题解析
19. 如图，方格纸中每个小方格都是边长为1的正方形，我们把以格点的连线为边的多边形称为“格点多边形”，如图中四边形 $A B C D$ 就是一个“格点四边形”．

(1)、在图中的方格纸中画一个格点四边形，使该四边形与原四边形 $A B C D$ 关于直线 $l$ 成轴对称；

(2)、求图中四边形 $A B C D$ 的面积．

查看试题解析
20. 如图，是一个材质均匀的转盘，转盘分成8个全等的扇形，颜色分为红、绿、黄三种，指针的位置固定，转动转盘后任其自由停止，（若指针指向两个扇形的交线时，当作指向右边的扇形），转动一次转盘：

(1)、求指针指向绿色扇形的概率；

(2)、指针指向红色扇形的概率大，还是绿色扇形概率大？为什么？

查看试题解析
21. 请把下面的说理过程补充完整：
已知：如图，CD平分∠ACB ， $A C / / D E ， C D / / E F$ ，那么EF平分∠DEB吗？请说明理由．
解：EF平分∠DEB．理由如下：
∵CD平分∠ACB（已知），
∴∠DCA＝∠DCE（角平分线的定义），
∵ $A C / / D E$ （已知），
∴∠DCA＝    ▲     ，
∴∠DCE＝∠CDE（等量代换），
∵ $C D / / E F$ （已知），
∴    ▲    ＝∠CDE（），∠DCE＝∠BEF（），
∴    ▲    ＝    ▲    （等量代换），
∴EF平分∠DEB（）

查看试题解析

22. 已知小明家、超市、体育场依次在同一条直线上，超市离家3km，体育场离家5km，小明从家出发，匀速骑行0.2h到达超市；在超市停留0.2h后，匀速骑行0.1h到达体育场；在体育场锻炼一段时间后，匀速骑行回到家，下面绘出的图象反映了这个过程中小明离家的距离与离开家的时间之间的对应关系，请根据相关信息解答下列问题：

(1)、依据题中提供的信息将下列表格补充完整：

离开家的时间／h	0.3	0.5	1	1.8
离家的距离／km			5

(2)、依据题中提供的信息填空：

①小明从超市骑行到体育场的速度为km/h；

②当小明离家的距离为2km时，他离开家的时间为

查看试题解析

23. 如图1，在△ABC中，AB＝AC，D是BC的中点，过点B作BE⊥AC，垂足为E，连接AD交BE于点F．

(1)、猜想∠CBE与∠CAD的数量关系，并说明理由；

(2)、P是射线EB上的点，过点C作 $C G / / E B$ 交PD的延长线于点G ．
①如图2，若点P在EB的延长线上，请说明PE＝BE＋CG的理由；

②当P在射线EB上运动时，若BE＝3，CG＝1.5，则PE＝ ▲ ．

查看试题解析

x	30	45	55	80	…
y	50	80	100	150	…