辽宁省阜新市海州区2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、选择题（在每一小题给出的四个选项中，只有一个是正确的．每题3分，共30分）

1. 若分式 $\frac{x}{x - 3}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \neq 3$ B、 $x < 3$ C、 $x > 3$ D、 $x \neq 3$ 且 $x \neq 0$

查看试题解析
2. 瓷器上的纹饰是中国古代传统文化的重要载体之一，下面花纹图案中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 平行四边形的周长为 $16 c m$ ，其中一边长为 $5 c m$ ，则它的邻边长为（）

A、 $3 c m$ B、 $5 c m$ C、 $6 c m$ D、 $9 c m$

查看试题解析
4. 用反证法证明命题“若在 $△ A B C$ 中， $A B \neq A C$ ，则 $∠ B \neq ∠ C$ ”时，首先应假设（）

A、 $∠ A = ∠ B$ B、 $A B = A C$ C、 $∠ A = ∠ C$ D、 $∠ B = ∠ C$

查看试题解析
5. 若一个正多边形的每个内角都是 $135 °$ ，则这个正多边形是（）

A、正六边形 B、正七边形 C、正八边形 D、正九边形

查看试题解析
6. 如图，在 $△ A B C$ 中， $D ， E ， F$ 分别是 $B C ， A C ， A B$ 的中点．若 $A B = 6 ， B C = 8$ ，四边形 $B D E F$ 的周长是（）

A、28 B、14 C、10 D、7

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B$ 、 $A C$ 的垂直平分线分别交 $B C$ 于点 $E$ 、 $F$ ，若 $△ A B C$ 的周长是20， $A B = 4 ， A C = 7$ ，则 $△ A E F$ 的周长为（）

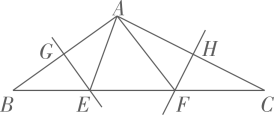A、4 B、7 C、9 D、11

查看试题解析
8. 若不等式组 ${\begin{cases} x + 6 > 4 x - 3 \\ x < m \end{cases}$ 的解集是 $x < 3$ ，则 $m$ 的取值范围是（）

A、 $m > 3$ B、 $m \geq 3$ C、 $m \leq 3$ D、 $m < 3$

查看试题解析
9. 已知 $a$ 、 $b$ 、是三角形的三条边，那么代数式 ${(a - b)}^{2} - c^{2}$ 的值（）

A、大于0 B、等于0 C、小于0 D、无法确定

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中， $∠ A B C$ 的角平分线交 $A D$ 于点 $E$ ， $∠ B C D$ 的角平分线交 $A D$ 于点 $F$ ，若 $A B = 7$ ， $B C = 10$ ，则 $E F$ 的长为（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题（每题3分，共24分）

11. 若分式 $\frac{x + 1}{x - 2}$ 的值等于0，则 $x$ 的值是.

查看试题解析
12. 多项式 $9 a^{2} b - 3 a b^{2}$ 中各项的公因式是.

查看试题解析
13. 若不等式 $(m - 4) x > m - 4$ 的解集为 $x < 1$ ，则 $m$ 的取值范围是.

查看试题解析
14. 对于命题“全等三角形的对应角相等”，它的逆命题是命题．（填“真”或“假”）

查看试题解析
15. 如图， $R t △ A B C$ 中， $A C = 8 ， B C = 15 ， A B = 17$ ，则内部五个小直角三角形的周长和为.

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ A B C$ 和 $∠ A C B$ 的平分线交于点 $D ， D E ⊥ B C$ 于点 $E$ ，如果 $D E = 1 ， △ A B C$ 的面积是6，则 $△ A B C$ 的周长是.

查看试题解析
17. 若关于 $x$ 的方程 $\frac{x}{x + 2} = \frac{m + 2}{2 x + 4}$ 有增根，则 $m$ 的值是.

查看试题解析
18. 如图，将 $△ A B C$ 绕点 $A$ 顺时针旋转 $a$ 度，得到 $△ A E D$ ，若点 $D$ 恰好在 $C B$ 的延长线上，则 $∠ B D E$ 等于度（用含有 $a$ 的代数式表示）．

查看试题解析

三、解答题（19题18分，20、21题每题8分，22、23题每题10分，24题12分，共66分）

19.

(1)、因式分解： $a^{2} (x - y) + 4 b^{2} (y - x)$ ．

(2)、解不等式组： ${\begin{array}{l} 3 x - 2 < x + 2 \\ \frac{x - 1}{2} \geq - 1 \end{array}$

(3)、先化简 $(1 - \frac{3}{x + 2}) \div \frac{x - 1}{x^{2} + 2 x}$ ，再从 $- 3 < x < 2$ 中选取一个合适的整数代入求值．

(4)、解分式方程： $\frac{x}{x - 2} - \frac{3}{2 x - 4} = \frac{1}{2}$ ．

查看试题解析
20. 如图，在平面直角坐标系中， $△ A B C$ 的顶点 $A (0 ， 1)$ ， $B (3 ， 2)$ ， $C (1 ， 4)$ 均在正方形网格的格点上．

⑴把 $△ A B C$ 绕点 $A$ 逆时针旋转 $90 °$ 得到 $△ A B_{1} C_{1}$ ，画出 $△ A B_{1} C_{1}$ ；

⑵直接写出点 $B$ 关于点 $O$ 中心对称的点的坐标；

⑶在 $x$ 轴上找一点 $P$ ，使得 $P A + P B$ 最小，请在图中标出点 $P$ 的位置，并直接写出这个最小值．

查看试题解析
21. 某地理兴趣小组负责老师暑假带领该小组同学去旅游参观，甲、乙两家旅行社的服务质量相同，且报价都是每人1200元，甲旅行社表示：“若老师全价，则学生可享受半价优惠。”乙旅行社表示：“包括老师在内都享受六折优惠。”设学生人数为 $x$ 人，甲旅行社收费为 $y_{甲}$ 元、乙旅行社收费为 $y_{乙}$ 元．

(1)、分别写出两家旅行社的收费与学生人数之间的关系式；

(2)、该老师选择哪一家旅行社支付的旅游费用较少？

查看试题解析
22. 如图， $▱ A B C D$ 的对角线 $A C ， B D$ 相交于点 $O ， E ， F$ 分别是 $O B ， O D$ 的中点，连接AE ， $A F ， C E ， C F$ ．

(1)、求证：四边形 $A E C F$ 是平行四边形；

(2)、若 $A B ⊥ A C ， A B = 3 ， B C = 5$ ．求 $B D$ 的长．

查看试题解析
23. 某中学计划购买 $A$ 、 $B$ 两种学习用品奖励学生，已知购买一个 $A$ 比购买一个 $B$ 多用2元，若用30元购买 $A$ 的数量和用24元购买 $B$ 数量相等．求 $A$ 、 $B$ 两种学习用品每件各需多少？

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ A C B = 90 ° ， A C = B C$ ，点 $M$ 是 $A B$ 的中点，点 $D$ 在 $B M$ 上， $A E ⊥ C D$ ， $B F ⊥ C D$ ，垂足分别为 $E ， F$ ，连接 $M E ， M F$ ．

(1)、求证： $C E = B F$ ；

(2)、求证： $△ E F M$ 是等腰直角三角形；

(3)、试判断线段 $D E ， D F ， D M$ 之间有何数量关系？直接写出你的结论．

查看试题解析