辽宁省抚顺市望花区2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）

1. 若式子 $\sqrt{\frac{1}{x}}$ 有意义，则（）

A、 $x > 0$ B、 $x \geq 0$ C、 $x \neq 0$ D、x为任意实数

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{15}$ C、 $\sqrt{27}$ D、 $\sqrt{40}$

查看试题解析
3. 如图，公路 $A C$ 、 $B C$ 互相垂直，公路 $A B$ 的中点M与点C被湖隔开，若测得 $A B$ 的长为 $4.8 k m$ ，则M、C两点间的距离为（　　）

A、 $2.4 k m$ B、 $3.6 k m$ C、 $4.2 k m$ D、 $4.8 k m$

查看试题解析
4. 在一次函数 $y = k x + 2$ 中， $y$ 的值随着 $x$ 值的增大而减小，则点 $P (3 ， k)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，数轴上点 $A$ 表示的数为 $- 1$ ， $R t △ A B C$ 的直角边 $A B$ 落在数轴上，且 $A B$ 长为3个单位长度， $B C$ 长为1个单位长度，若以点 $A$ 为圆心，以斜边 $A C$ 长为半径画弧交数轴于点 $D$ ，则点 $D$ 表示的数为（）

A、 $\sqrt{10}$ B、 $\sqrt{5} - 1$ C、 $\sqrt{5}$ D、 $\sqrt{10} - 1$

查看试题解析
6. 小明参加“强国有我”主题演讲比赛，其演讲形象、内容、效果三项的成绩分别是 $70$ 分、 $90$ 分、 $80$ 分，若将三项得分依次按 $2$ ： $4$ ： $4$ 的比例确定最终成绩，则小明的最终比赛成绩为（）

A、 $70$ 分 B、 $80$ 分 C、 $82$ 分 D、 $90$ 分

查看试题解析
7. 两张全等的矩形纸片 $A B C D$ ， $A E C F$ 按如图所示的方式交叉叠放， $A B = A F$ ， $A E = B C . A E$ 与 $B C$ 交于点 $G$ ， $A D$ 与 $C F$ 交于点 $H$ ，且 $∠ A G B = 30 °$ ， $A B = 2$ ，则四边形 $A G C H$ 的周长为（）

A、 $4$ B、 $8$ C、 $12$ D、 $16$

查看试题解析
8. 某油箱容量为 $50 L$ 的汽车，加满汽油后开了 $200 k m$ 时，油箱中的汽油大约消耗了四分之一，如果加满汽油后汽车行驶的路程为 $x | k m$ ，油箱中的剩油量为 $y | L$ ，则 $y$ 与 $x$ 之间的函数解析式和自变量取值范围分别是（）

A、 $y = 0.0625 x$ ， $x > 0$ B、 $y = 50 - 0.0625 x$ ， $x > 0$ C、 $y = 0.0625 x$ ， $0 \leq x \leq 800$ D、 $y = 50 - 0.0625 x$ ， $0 \leq x \leq 800$

查看试题解析
9. 已知 $M$ ， $N$ 是线段 $A B$ 上的两点， $A M = M N = 2$ ， $N B = 1$ ，以点 $A$ 为圆心， $A N$ 长为半径画弧；再以点 $B$ 为圆心， $B M$ 长为半径画弧，两弧交于点 $C$ ，则 $△ A B C$ 一定是（）

A、直角三角形 B、等腰直角三角形 C、锐角三角形 D、钝角三角形

查看试题解析
10. 如图1，点 $E$ 为矩形 $A B C D$ 中 $A D$ 边的中点，点 $P$ 从点 $A$ 出发，沿 $A \to E \to B$ 以 $2 cm / s$ 的速度运动到点 $B$ ，图2是点 $P$ 运动时， $△ PBC$ 的面积 $y ({cm}^{2})$ 随时间 $t (s)$ 变化的函数图象，则 $a$ 的值为（）

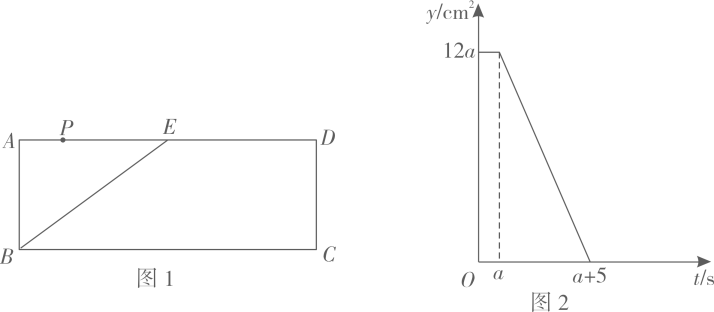A、5 B、4 C、3 D、2

查看试题解析

二、填空题（本大题共8小题，共16.0分）

11. 实数 $a$ 在数轴上的位置如图所示，化简 $\sqrt{a^{2}} - a$ 等于．

查看试题解析
12. 已知： $x = \sqrt{13} + 1 ， y = \sqrt{13} - 1$ ，则 $x y$ 的值为．

查看试题解析
13. 命题“如果两个实数都是正数，那么它们的积也是正数”的逆命题是命题 $. ($ 填“真”或“假” $)$

查看试题解析
14. 某校举行体操比赛，甲、乙两个班各选 $18$ 名学生参加比赛，两个班参赛学生的平身高都是 $1.72$ 米，其方差分别是 $S_{甲}^{2} = 3.24$ ， $S_{乙}^{2} = 1.63$ ，则参赛学生身高比较整齐的班级是班 $.$

查看试题解析
15. 将直线 $y = 4 x - 3$ 向下平移 $2$ 个单位长度，得到的直线解析式是．

查看试题解析
16. 如图，在一束平行光线中插入一张对边平行的纸板，如果光线与纸板右下方所成的 $∠ 1$ 是 $72 ° 15'$ ，那么光线与纸板左上方所成的 $∠ 2$ 的度数是．

查看试题解析
17. 毕达哥拉斯树也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树状图形，其中所有的四边形都是正方形，所有的三角形都是直角三角形 $.$ 如图，若正方形 $A$ 、 $B$ 、 $C$ 、 $D$ 的边长分别是 $2$ ， $3$ ， $1$ ， $2$ ，则正方形 $G$ 的边长是．

查看试题解析
18. 如图，在菱形 $A B C D$ 中， $∠ B A D = 60 °$ ， $A C$ 与 $B D$ 交于点 $O$ ，点 $E$ 为 $C D$ 延长线上一点，且 $C D = D E$ ，连接 $B E$ ，分别交 $A C$ 、 $A D$ 于点 $F$ 、点 $G$ ，连接 $O G$ 、 $A E$ ，则下列结论：

      $① O G = \frac{1}{2} A B$ ；

      $②$ 四边形 $A B D E$ 是菱形；

      $③$ 四边形 $O D E G$ 与四边形 $O B A G$ 面积相等．

其中正确的结论有个 $.$

查看试题解析

三、解答题（本大题共8小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）

19. 计算：

(1)、 $(\sqrt{5} - 1)^{2} + \sqrt{20}$ ；

(2)、 $\sqrt{3} (\sqrt{2} + \sqrt{6}) - \sqrt{24} \div \sqrt{3}$ ．

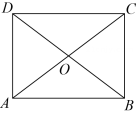
查看试题解析
20. 某景点门票销售分两类：一类为散客门票，价格为 $40$ 元 $/$ 张；另一类为团体门票 $($ 一次购买门票 $10$ 张及以上 $)$ ，每张门票价格在散客门票基础上打 $8$ 折 $.$ 某班部分同学要去该景点旅游，设参加旅游 $x$ 人，购买门票需要 $y$ 元．

(1)、如果买团体票，写出 $y$ 与 $x$ 之间的函数解析式，并写出自变量取值范围；

(2)、根据人数变化设计比较省钱的购票方案．

查看试题解析
21. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，且 $O A = O D .$ 若 $∠ O A D = 50 °$ ，求 $∠ O A B$ 的度数．

查看试题解析
22. 某校八年级 $(1)$ 班的小华和小轩学习了“勾股定理”之后，为了测得风筝的垂直高度 $C E$ ，他们进行了如下操作：

      $①$ 测得水平距离 $B D$ 的长为 $12 m$ ；

      $②$ 根据手中剩余线的长度计算出风筝线 $B C$ 的长为 $20 m$ ；

      $③$ 牵线放风筝的小明的身高 $(A B)$ 为 $1.62 m$ ．

(1)、如图 $1$ 是放风筝的示意图，其中点 $C$ 、 $D$ 、 $E$ 在同一条直线上，且 $B A ⊥ A E$ ， $C E ⊥ A E$ ， $B D ⊥ C E$ ，垂足为点 $D$ ，请根据题意，求出风筝的垂直高度 $C E$ ；

(2)、如果小明想让风筝沿 $C D$ 方向下降 $11 m$ ，则他应该往回收线多少米？

查看试题解析

23. 某校对八年级的

400

名学生进行了一次体育测试

.

测试完成后，在甲、乙两班各抽取了

20

名学生的测试成绩，对数据进行整理分析，并给出了下列信息：

甲班 $20$ 名同学的测试成绩统计如下： $41$ ， $47$ ， $43$ ， $45$ ， $50$ ， $49$ ， $48$ ， $50$ ， $50$ ， $49$ ， $48$ ， $47$ ， $44$ ， $50$ ， $43$ ， $50$ ， $50$ ， $50$ ， $49$ ， $47$ ．

乙班 $20$ 名同学的测试成绩统计如下：

组别	$40 < x \leq 42$	$42 < x \leq 44$	$44 < x \leq 46$	$46 < x \leq 48$	$48 < x \leq 50$
频数	$1$	$1$	$a$	$6$	$9$

其中，乙班 $20$ 名同学的测试成绩高于 $46$ ，但不超过 $48$ 分的成绩如下： $47$ ， $48$ ， $48$ ， $47$ ， $48$ ， $48$ ．

甲、乙两班抽取的学生的测试成绩的平均数、中位数、众数如表所示：

班级	平均数	中位数	众数
甲班	$47.5$	$48.5$	$c$
乙班	$47.5$	$b$	$49$

(1)、根据以上信息可以写出：

a =

，

b =

，

c =

；

(2)、你认为甲、乙两个班哪个班的学生体育测试成绩较好，请说明理由；

(3)、若规定

49

分及以上为优秀，请估计该校八年级参加此次测试的学生中优秀的学生有多少人．

查看试题解析

24. 如图所示，在同一个坐标系中，一次函数 $y = k_{1} x + b_{1}$ 和 $y = k x + b$ 的图象分别与 $x$ 轴交于点 $A$ ，点 $B$ ，两直线相交于点 $C$ ，已知点 $A$ 坐标为 $(- 1 ， 0)$ ，点 $B$ 的坐标为 $(2 ， 0)$ ，观察象并回答下列问题：

(1)、关于 $x$ 的方程 $k_{1} x + b_{1} = 0$ 的解是，关于 $x$ 的不等式 $k x + b < 0$ 的解集是；

(2)、直接写出：关于 $x$ 的不等式组 ${\begin{array}{l} k x + b > 0 \\ k_{1} x + b_{1} > 0 \end{array}$ 的解集是；

(3)、若点 $C$ 坐标为 $(1 ， 3)$ ，
$①$ 关于 $x$ 的不等式 $k_{1} x + b_{1} > k x + b$ 的解集是 ▲ ；

$②$ 请求出 $△ A B C$ 的面积．

查看试题解析
25. 已知四边形 $A B C D$ 是正方形，点 $E$ 、点 $F$ 分别是边 $B C$ 、 $A B$ 所在的直线上的点， $C E = B F$ ，连接 $D E$ 、 $C F$ ， $D E$ 与直线 $C F$ 相交于点 $H$ ，过点 $E$ 作 $E G ⊥ D E$ ，并且使 $E G = D E$ ，连接 $F G$ ．

(1)、如图 $1$ ，当点 $E$ 、点 $F$ 分别在 $B C$ 、 $A B$ 边上时， $F G$ 与 $C E$ 的数量关系是；位置关系是；

(2)、如图 $2$ ，当点 $E$ 、点 $F$ 分别在 $C B$ 、 $B A$ 延长线上时， $(1)$ 中结论是否仍然成立？若成立请予以证明：若不成立，请说明理由；

(3)、如图 $3$ ，当点 $E$ 、点 $F$ 分别在 $B C$ 、 $A B$ 延长线时， $(1)$ 中结论是否仍然成立？请直接写出你的结论．

查看试题解析
26. 如图 $1$ ，在平面直角坐标系中，一次函数 $y = 2 x + 6$ 的图象交 $x$ 轴于点 $A$ ，交 $y$ 轴于点 $B .$ 点 $D$ 在 $x$ 轴正半轴上，且 $O D = \frac{8}{3} O A$ ，以 $A B$ 、 $A D$ 为边作平行四边形 $A B C D$ ．

(1)、点 $A$ 的坐标，点 $B$ 的坐标；

(2)、请求出直线 $B D$ 的函数解析式；

(3)、如图 $2$ ，点 $E$ 从点 $O$ 出发，以每秒 $1$ 个单位的速度沿 $x$ 轴正方向移动，记点 $E$ 运动时间为 $t$ 秒 $.$ 点 $F$ 是线段 $B D$ 的中点，连接 $E F$ 并延长交直线 $B C$ 于点 $H$ ，请直接写出：当 $t$ 为何值时，四边形 $A B H E$ 为平行四边形；

(4)、点 $Q$ 是直线 $B D$ 上的一个动点，在 $y$ 轴上找一点 $P$ ，连接 $A P$ ， $A Q$ ， $P Q$ ，当 $△ A P Q$ 是以 $P Q$ 为斜边的等腰直角三角形时，请直接写出点 $P$ 的坐标．

查看试题解析