辽宁省丹东市凤城市2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录,下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 多项式8a3b2+12ab3c的公因式是( )A、abc B、4ab2 C、ab2 D、4ab2c3. 等腰三角形的一个角是80°,则它顶角的度数是( )A、80° B、80°或20° C、80°或50° D、20°4. 一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )A、360° B、540° C、720° D、900°5. 把分式(x≠0,y≠0)中的分子、分母的x、y同时扩大为原来的2倍,那么分式的值( )A、扩大为原来的2倍 B、扩大为原来的4倍 C、缩小为原来的 D、不改变6. 下列命题为真命题的是( )A、若ab>0,则a>0,b>0 B、两个锐角分别相等的两个直角三角形全等 C、在一个角的内部,到角的两边距离相等的点在这个角的平分线上 D、一组对边平行,另一组对边相等的四边形是平行四边形7. 已知 , 则的值等于( )A、 B、 C、 D、8. 若关于的方程的解为正数,则的取值范围是( )A、 B、且 C、 D、且9. 如图,在▱中,以点为圆心,适当长度为半径作弧,分别交 , 于点 , , 再分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , 作射线交于点 , 连接若 , , , 则▱的面积为( )
2. 多项式8a3b2+12ab3c的公因式是( )A、abc B、4ab2 C、ab2 D、4ab2c3. 等腰三角形的一个角是80°,则它顶角的度数是( )A、80° B、80°或20° C、80°或50° D、20°4. 一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )A、360° B、540° C、720° D、900°5. 把分式(x≠0,y≠0)中的分子、分母的x、y同时扩大为原来的2倍,那么分式的值( )A、扩大为原来的2倍 B、扩大为原来的4倍 C、缩小为原来的 D、不改变6. 下列命题为真命题的是( )A、若ab>0,则a>0,b>0 B、两个锐角分别相等的两个直角三角形全等 C、在一个角的内部,到角的两边距离相等的点在这个角的平分线上 D、一组对边平行,另一组对边相等的四边形是平行四边形7. 已知 , 则的值等于( )A、 B、 C、 D、8. 若关于的方程的解为正数,则的取值范围是( )A、 B、且 C、 D、且9. 如图,在▱中,以点为圆心,适当长度为半径作弧,分别交 , 于点 , , 再分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , 作射线交于点 , 连接若 , , , 则▱的面积为( )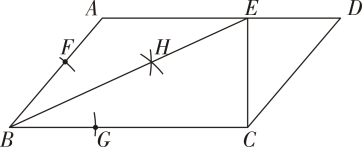 A、 B、 C、 D、10. 如图,为一副重叠放置的三角板,其中 , 与共线,将沿方向平移,当经过的中点时,直线交于点 , 若 , 则此时的长度为( )
A、 B、 C、 D、10. 如图,为一副重叠放置的三角板,其中 , 与共线,将沿方向平移,当经过的中点时,直线交于点 , 若 , 则此时的长度为( )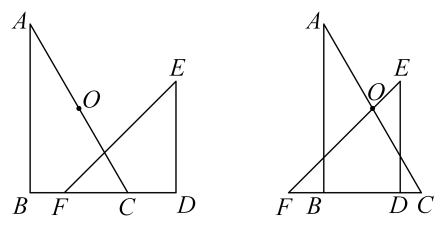 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
11. 函数 的自变量x的取值范围是 .
12. 因式分解:= .13. 如图,在平面直角坐标系中,函数与的图象交于点 , 则不等式的解集为 .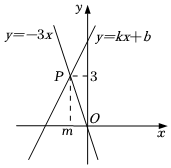 14. 如图,、、、是五边形的外角,且 , 则的度数是 .
14. 如图,、、、是五边形的外角,且 , 则的度数是 . 15. 如图,是的边的中点,平分 , 于点 , 延长交于点 , 已知 , , , 则的周长是 .
15. 如图,是的边的中点,平分 , 于点 , 延长交于点 , 已知 , , , 则的周长是 . 16. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为.
16. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为.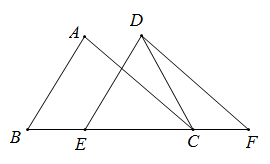 17. 如图,在▱中, , , , 垂足分别为点 , , 则 .
17. 如图,在▱中, , , , 垂足分别为点 , , 则 .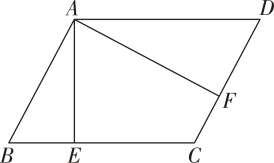 18. 如图,在中, , , , 点为上一点,将线段绕点顺时针旋转得线段 , 点在射线上,当的垂直平分线经过一边中点时,的长为 .
18. 如图,在中, , , , 点为上一点,将线段绕点顺时针旋转得线段 , 点在射线上,当的垂直平分线经过一边中点时,的长为 .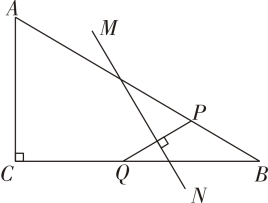
三、计算题(本大题共1小题,共6.0分)
-
19. 解方程: .
四、解答题(本大题共7小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
-
20. 已知实数 , 满足 , 求代数式的值.21. 如图,正方形网格中每个小正方形边长都是一个单位长度,在平面直角坐标系中,为三个顶点分别是 , , .

⑴画出向左平移个单位得到的;
⑵画出绕点逆时针旋转后得到的;
⑶在平面上存在点 , 使得以、、、为顶点的四边形是平行四边形,请直接写出符合条件的所有点的坐标.
22. 如图,在中, , 是的垂直平分线,垂足为 , 交于点 . (1)、若 , 求的度数;(2)、若的周长为 , 的长为 , 求的周长23. 如图,已知 , 、、、在一条直线上, , .
(1)、若 , 求的度数;(2)、若的周长为 , 的长为 , 求的周长23. 如图,已知 , 、、、在一条直线上, , .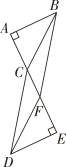
求证:
(1)、≌;(2)、四边形是平行四边形.24. 为了能够更好地进行居家电路实验学习,某校九年级班在电商平台上购买小电动机和小灯泡已知该平台上一个小电动机与一个小灯泡的价格之和是元,同学们决定用元购买小灯泡,元购买小电动机,其中购买的小灯泡数量正好是小电动机数量的倍.(1)、分别求出每个小灯泡和小电动机的价格.(2)、若九年级(1)班决定购买小灯泡和小电动机共计个,且满足小灯泡数量不超过小电动机数量的一半,请设计出更省钱的购买方案,并求出总费用的最小值.25. 如图1,在平面直角坐标系xOy中,有长方形OABC,其中点C坐标为 , , 点D是边OC的中点,点P是射线CA上的一个动点,请回答下面的问题: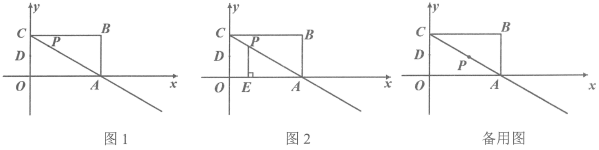 (1)、若点P是线段AC的中点,直接写出 .(2)、如图2,过点P作轴,垂足是点E,若以C、D、E、P为顶点的四边形是平行四边形,求出点P的坐标.(3)、连接BP,若是等腰三角形,求CP的长度.26. 如图 , 为等边三角形,在、上分别取点、 , 使 , 连接 .
(1)、若点P是线段AC的中点,直接写出 .(2)、如图2,过点P作轴,垂足是点E,若以C、D、E、P为顶点的四边形是平行四边形,求出点P的坐标.(3)、连接BP,若是等腰三角形,求CP的长度.26. 如图 , 为等边三角形,在、上分别取点、 , 使 , 连接 .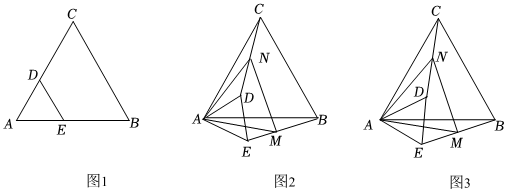 (1)、求证:是等边三角形.(2)、点、分别是、的中点,连接 , 当绕点旋转到如图的位置时,求的度数.(3)、在(2)条件下,若 , , , 求的长.
(1)、求证:是等边三角形.(2)、点、分别是、的中点,连接 , 当绕点旋转到如图的位置时,求的度数.(3)、在(2)条件下,若 , , , 求的长.
-