辽宁省本溪市本溪县2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本题共10小题,每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列图形中不是轴对称图形的是( )A、
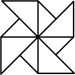 B、
B、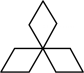 C、
C、 D、
D、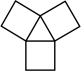 2. 下列运算正确的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、“打开电视,正在播放本溪新闻节目”是必然事件 B、某种彩票中奖率为10%是指买十张一定有一张中奖 C、“明天降雨的概率是50%”表示明天有半天都在降雨 D、“掷一次骰子,向上一面的点数是6”是随机事件4. 一个三角形三个内角的度数之比为 , 则这个三角形一定是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形5. 是完全平方式,则常数k等于( )A、64 B、48 C、32 D、166. 如图,直线 , , , 则的度数为( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、“打开电视,正在播放本溪新闻节目”是必然事件 B、某种彩票中奖率为10%是指买十张一定有一张中奖 C、“明天降雨的概率是50%”表示明天有半天都在降雨 D、“掷一次骰子,向上一面的点数是6”是随机事件4. 一个三角形三个内角的度数之比为 , 则这个三角形一定是( )A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形5. 是完全平方式,则常数k等于( )A、64 B、48 C、32 D、166. 如图,直线 , , , 则的度数为( ) A、50° B、60° C、65° D、75°7. 已知的底边BC上的高8cm,当它的底边BC从16cm变化到5cm时,的面积( )A、从变化到 B、从变化到 C、从变化到 D、从变化到8. 如图,点D , E分别在线段AB , AC上,CD与BE相交于点O , 已知 , 现添加以下的哪个条件仍不能判定( )
A、50° B、60° C、65° D、75°7. 已知的底边BC上的高8cm,当它的底边BC从16cm变化到5cm时,的面积( )A、从变化到 B、从变化到 C、从变化到 D、从变化到8. 如图,点D , E分别在线段AB , AC上,CD与BE相交于点O , 已知 , 现添加以下的哪个条件仍不能判定( ) A、 B、 C、 D、9. 已知a , b , c是的三条边,化简的结果为( )A、 B、 C、 D、010. 如图,在正方形网格中,网格线的交点称为格点.已知A , B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A、 B、 C、 D、9. 已知a , b , c是的三条边,化简的结果为( )A、 B、 C、 D、010. 如图,在正方形网格中,网格线的交点称为格点.已知A , B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( ) A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题(本题共8小题,每小题2分,共16分)
-
11. 若 , 则a的取值范围是 .12. 已知 , 则的补角为 .13. 一个不透明的布袋中,放有3个白球,5个红球,它们除颜色外完全相同,从中随机摸取一个,摸到红球的概率是 .14. 如图,在中,AD为BC边上的中线,若与的周长差为3, , 则 .
 15. 若x+=3,则x2+= .
15. 若x+=3,则x2+= .
16. 若 , 则 .17. 如图,在中,BO平分 , 平分 , 若 , 则 . 18. 如图,在中, , , 以点C为圆心,CA长为半径作弧,交直线BC于点P , 连接AP , 则的度数是 .
18. 如图,在中, , , 以点C为圆心,CA长为半径作弧,交直线BC于点P , 连接AP , 则的度数是 .
三、解答题(第19题12分,第20题6分,21题6分共24分)
-
19. 计算:(1)、(2)、(3)、20. 先化简,再求值: , 其中 , .21. 如图,在正方形网格上有一个 .
 (1)、画出关于直线MN的对称图形(不写画法);(2)、若网格上的每个小正方形的边长为1,求的面积.
(1)、画出关于直线MN的对称图形(不写画法);(2)、若网格上的每个小正方形的边长为1,求的面积.四、解答题(本大题共2小题,第22题6分,第23题6分,共12分)
-
22. 如图, , 点E是CD上一点, , EF平分交AB于点F , 求的度数.
 23. 如图,D是的边AB上一点,DF交AC于点E , , . 试说明 .
23. 如图,D是的边AB上一点,DF交AC于点E , , . 试说明 .
五、解答题(本大题8分)
-
24. 如图是小明骑自行车离家的距离与时间之间的关系.
 (1)、在这个变化过程中自变量是 , 因变量是;(2)、小明何时到达离家最远的地方?此时离家多远?(3)、小明何时与家相距20km?
(1)、在这个变化过程中自变量是 , 因变量是;(2)、小明何时到达离家最远的地方?此时离家多远?(3)、小明何时与家相距20km?六、解答题(本大题10分)
-
25. 国家规定,中小学生每天在校体育活动时间不低于1h , 为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间进行分组(A组: , B组: , C组: , D组:),绘制成如图所示的两幅不完整统计图,请根据图中信息回答问题:
 (1)、此次抽查的学生为人;(2)、补全条形统计图;(3)、从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是多少?(4)、若当天在校学生为1600人,请估计在当天达到国家规定体育活动时间的学生有多少人.
(1)、此次抽查的学生为人;(2)、补全条形统计图;(3)、从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是多少?(4)、若当天在校学生为1600人,请估计在当天达到国家规定体育活动时间的学生有多少人.七、解答题(本大题10分)
-
26. 已知 , , , , 垂足分别为点D , E .
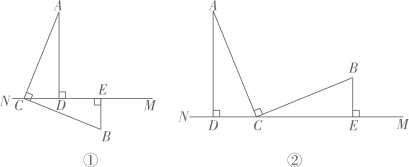 (1)、如图①,求证:(2)、如图②,(1)中的结论还成立吗?如果不成立,请写出线段AD , BE , DE之间的数量关系,并说明理由.
(1)、如图①,求证:(2)、如图②,(1)中的结论还成立吗?如果不成立,请写出线段AD , BE , DE之间的数量关系,并说明理由.
-
-