辽宁省抚顺市清原县2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{7}$ B、 $\sqrt{8}$ C、 $\sqrt{9}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 下列各组数中，是勾股数的是（）

A、 $1$ ， $1$ ， $\sqrt{2}$ B、 $3^{2}$ ， $4^{2}$ ， $5^{2}$ C、 $9$ ， $12$ ， $15$ D、 $1.5$ ， $2$ ， $2.5$

查看试题解析
3. 下列运算结果正确的是（）

A、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$ B、 $2 + 3 \sqrt{2} = 5 \sqrt{2}$ C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$

查看试题解析
4. 已知函数 $y = (m + 2) x^{m^{2} - 3}$ 是正比例函数，则 $m$ 的值是（）

A、 $2$ B、 $- 2$ C、 $\pm 2$ D、 $\frac{1}{2}$

查看试题解析
5. 小红在“养成阅读习惯，快乐阅读，健康成长”读书大赛活动中，随机调查了本校初二年级20名同学，在近5个月内每人阅读课外书的数量，数据如下表所示：
人数
3
4
8
5
课外书数量（本）
12
13
15
18
则阅读课外书数量的中位数和众数分别是（）

A、13，15 B、14，15 C、13，18 D、15，15

查看试题解析
6. 根据图象，可得关于 $x$ 的不等式 $k x > - x + 3$ 的解集是（）

A、 $x < 2$ B、 $x > 2$ C、 $x < 1$ D、 $x > 1$

查看试题解析
7. 已知▱ $A B C D$ ，根据图中尺规作图的痕迹，判断下列结论中不一定成立的是（）

A、 $∠ D A E = ∠ B A E$ B、 $∠ D E A = \frac{1}{2} ∠ D A B$ C、 $D E = B E$ D、 $B C = D E$

查看试题解析
8. 如图，有两棵树，一棵高 $10$ 米，另一棵高 $4$ 米，两树相距 $8$ 米 $.$ 一只鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行（）

A、 $6$ 米 B、 $8$ 米 C、 $10$ 米 D、 $12$ 米

查看试题解析
9. 如图， $O$ 为正方形 $A B C D$ 对角线 $A C$ 的中点， $△ A C E$ 为等边三角形．若 $A B = 2$ ，则 $O E$ 的长度为（）

A、 $\frac{\sqrt{6}}{2}$ B、 $\sqrt{6}$ C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

查看试题解析
10. 如图，在矩形纸片 $A B C D$ 中，点 $E$ 在 $B C$ 边上，将 $△ C D E$ 沿 $D E$ 翻折得到 $△ F D E$ ，点 $F$ 落在 $A E$ 上.若 $C E = 3 c m$ ， $A F = 2 E F$ ，则AB= cm（）

A、 $2 \sqrt{5}$ B、 $3 \sqrt{5}$ C、 $\sqrt{5}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析

二、填空题（本大题共8小题，共24.0分）

11. 式子 $\sqrt{a + 1}$ 有意义，则实数 $a$ 的取值范围是．

查看试题解析
12. 一组数据 $2$ ， $5$ ， $8$ ， $3$ ， $5$ ， $1$ 的中位数是．

查看试题解析
13. 一组数据 $1$ 、 $2$ 、 $3$ 、 $4$ 、 $5$ 的方差是．

查看试题解析
14. 某校举行科技创新比赛，按照理论知识占 $20 %$ ，创新设计占 $50 %$ ，现场展示占 $30 %$ 这样的比例计算选手的综合成绩 $.$ 某同学本次比赛的各项成绩分别为理论知识 $95$ 分，创新设计 $88$ 分，现场展示 $90$ 分，则该同学的综合成绩是分．

查看试题解析
15. 若一次函数 $y = 2 x + 1$ 的图象经过点 $(- 3 ， y_{1})$ ， $(4 ， y_{2})$ ，则 $y_{1}$ $y_{2} ($ 填“ $<$ ”或“ $>$ ” $)$ ．

查看试题解析
16. 我国古代数学著作 $《$ 九章算术 $》$ 中记载了一个问题：“今有池方一丈，葭 $(j i a)$ 生其中，出水一尺，引葭赴岸，适与岸齐 $.$ 问水深几何 $.$ ” $($ 丈、尺是长度单位， $1$ 丈 $= 10$ 尺 $)$ 其大意为：有一个水池，水面是一个边长为 $10$ 尺的正方形，在水池正中央有一根芦苇，它高出水面 $1$ 尺 $.$ 如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度是多少？则水深为．

查看试题解析
17. 如图，四边形 $A B C D$ 为菱形， $∠ A B C = 80 °$ ，延长 $B C$ 到 $E$ ，在 $∠ D C E$ 内作射钱 $C M$ ，使得 $∠ E C M = 30 °$ ，过点 $D$ 作 $D F ⊥ C M$ ，垂足为 $F .$ 若 $D F = \sqrt{6}$ ，则 $B D$ 的长为 $($ 结果保留根号 $)$ ．

查看试题解析
18. 如图，矩形 $A B C D$ ， $A B = 1$ ， $B C = 2$ ，点 $A$ 在 $x$ 轴正半轴上，点 $D$ 在 $y$ 轴正半轴上.当点 $A$ 在 $x$ 轴上运动时，点 $D$ 也随之在 $y$ 轴上运动，在这个运动过程中，点 $C$ 到原点 $O$ 的最大距离为 .

查看试题解析

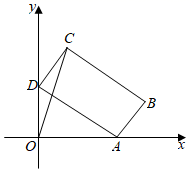
三、解答题（本大题共8小题，共76.0分。解答应写出文字说明，证明过程或演算步骤）

19. 计算：

(1)、 $\sqrt{12} - \sqrt{2} \times (\sqrt{8} - 3 \sqrt{\frac{1}{2}})$ ；

(2)、 $(\sqrt{5} + 3) (\sqrt{5} - 3) - (\sqrt{3} - 1)^{2}$ ．

查看试题解析

20. 某校团委组织了一次全校

2000

名学生参加的“中国诗词大会”海选比赛，赛后发现所有参赛学生的成绩均不低于

50

分

.

为了更好地了解本次海选比赛的成绩分布情况，随机抽取了其中

200

名学生的海选比赛成绩

(

成绩

x

取整数，总分

100

分

)

，作为样本进行整理，得到下列统计图表：

组别	海选成绩 $x$	频数
$A$ 组	$50 \leq x < 60$	$10$
$B$ 组	$60 \leq x < 70$	$30$
$C$ 组	$70 \leq x < 80$	$40$
$D$ 组	$80 \leq x < 90$	$b$
$E$ 组	$90 \leq x < 100$	$70$

(1)、在频数分布表中

b

的值是在图

2

的扇形统计图中，记表示

B

组人数所占的百分比为

a %

，则

a

的值为，表示

C

组扇形的圆心角的度数为度；

(2)、根据频数分布表，请估计所选取的

200

名学生的平均成绩；

(3)、规定海选成绩在

90

分以上

(

包括

90

分

)

记为“优等”，请估计该校参加这次海选比赛的

2000

名学生中成绩“优等”的有多少人．

查看试题解析

21. 学过 $《$ 勾股定理 $》$ 后，某班兴趣小组来到操场上测量旗杆 $A B$ 的高度，得到如下信息：
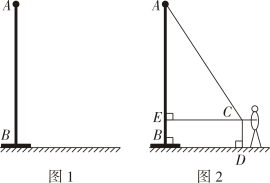
$①$ 测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长 $1$ 米 $($ 如图 $1)$ ；
$②$ 当将绳子拉直时，测得此时拉绳子的手到地面的距离 $C D$ 为 $1$ 米，到旗杆的距离 $C E$ 为 $6$ 米（如图2）．
根据以上信息，求旗杆 $A B$ 的高度．

查看试题解析
22. 如图，在菱形ABCD中， $A E ⊥ B C$ 于点E， $A F ⊥ C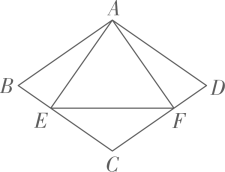 D$ 于点F，连结EF。

(1)、求证： $A E = A F$ ；

(2)、若 $∠ B = 60 °$ ，求 $∠ A E F$ 的度数。

查看试题解析
23. 某教育科技公司销售 $A$ ， $B$ 两种多媒体教学设备，这两种多媒体设备的进价与售价如表所示：该教育科技公司计划购进 $A$ ， $B$ 两种多媒体设备共 $50$ 套，设购进 $A$ 种多媒体设备 $x$ 套，利润为 $y$ 万元．

          $A$
          $B$
进价 $($ 万元 $/$ 套 $)$
          $3$
          $2.4$
售价 $($ 万元 $/$ 套 $)$
          $3.3$
          $2.8$

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、若公司要求购进 $B$ 种多媒体设备的数量不超过 $A$ 种多媒体设备的 $4$ 倍，当该公司把购进的两种多媒体设备全部售出，求购进 $A$ 种多媒体设备多少套时，能获得最大利润，最大利润是多少万元？

查看试题解析
24. 如图，四边形 $A B C D$ 是正方形，以 $C D$ 为边在正方形的外部作等边 $△ C D E$ ，连接 $B E$ ， $A C$ ， $B E$ 与 $A C$ 交于点 $M$ ，连接 $M D$ ．

(1)、求 $∠ C B E$ 的度数；

(2)、求证： $M E = M A$ ．

查看试题解析
25. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = - \frac{4}{3} x + 4$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 、点 $B$ ，点 $D$ 在 $y$ 轴的负半轴上，若将 $△ D A B$ 沿直线 $A D$ 折叠，点 $B$ 恰好落在 $x$ 轴正半轴上的点 $C$ 处．

(1)、求 $A B$ 的长；

(2)、求点 $C$ 和点 $D$ 的坐标；

(3)、 $y$ 轴上是否存在一点 $P$ ，使得 $S_{△ P A B} = \frac{1}{2} S_{△ O C D}$ ？若存在，直接写出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析
26. 在▱ $A B C D$ 中， $∠ C = 45 °$ ， $A D = B D$ ，点 $P$ 为射线 $C D$ 上的动点 $($ 点 $P$ 不与点 $D$ 重合 $)$ ，连接 $A P$ ，过点 $P$ 作 $E P ⊥ A P$ 交直线 $B D$ 于点 $E$ ．

(1)、如图 $①$ ，当点 $P$ 为线段 $C D$ 的中点时，请直接写出 $P A$ ， $P E$ 的数量关系；

(2)、如图 $②$ ，当点 $P$ 在线段 $C D$ 上时，求证： $D A + \sqrt{2} D P = D E$ ；

(3)、点 $P$ 在射线 $C D$ 上运动，若 $A D = 3 \sqrt{2}$ ， $A P = 5$ ，请直接写出线段 $B E$ 的长．

查看试题解析

	$A$	$B$
进价 $($ 万元 $/$ 套 $)$	$3$	$2.4$
售价 $($ 万元 $/$ 套 $)$	$3.3$	$2.8$

人数	3	4	8	5
课外书数量（本）	12	13	15	18