辽宁省丹东市凤城市2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是 , 这个数用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 下列各组图形中,是的高的图形是( )A、
2. 石墨烯是现在世界上最薄的纳米材料,其理论厚度仅是 , 这个数用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 下列各组图形中,是的高的图形是( )A、 B、
B、 C、
C、 D、
D、 5. 下列说法正确的是( )A、“守株待兔”是必然事件 B、“概率为的事件”是不可能事件 C、“在一个只装有个红球的袋中摸出个球是红球”是必然事件 D、任意掷一枚质地均匀的硬币次,正面向上的次数一定是次6. 如图,的垂直平分线交于点 , , , 则的周长为( )
5. 下列说法正确的是( )A、“守株待兔”是必然事件 B、“概率为的事件”是不可能事件 C、“在一个只装有个红球的袋中摸出个球是红球”是必然事件 D、任意掷一枚质地均匀的硬币次,正面向上的次数一定是次6. 如图,的垂直平分线交于点 , , , 则的周长为( ) A、 B、 C、 D、7. 如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是( )
A、 B、 C、 D、7. 如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是( ) A、ASA B、SAS C、AAS D、SSS8. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如表),下列说法中错误的是( )
A、ASA B、SAS C、AAS D、SSS8. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如表),下列说法中错误的是( )温度
声速
A、当空气温度为时,内声音可以传播 B、温度每升高 , 声速增加 C、在这个变化过程中,自变量是温度,因变量是声速 D、温度越高,声速越快9. 如图,在和中,如果 , 在下列条件中不能保证≌的是( ) A、 B、 C、 D、10. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三角形 , 改变三角板的位置其中点位置始终不变 , 当时, . ( )
A、 B、 C、 D、10. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三角形 , 改变三角板的位置其中点位置始终不变 , 当时, . ( ) A、 B、或 C、或 D、或
A、 B、或 C、或 D、或二、填空题(本大题共8小题,共24.0分)
-
11. 若 , , 则 .12. 若 , 则它的余角的补角等于度13. 一个等腰三角形的边长分别是4cm和9cm,则它的周长是cm.
14. 如图,一块飞镖游戏板由大小相等的小正方形格子构成.向游戏板随机投掷一枚飞镖(每次飞镖均落在纸板上),击中阴影区域的概率是 . 15. 将直尺与三角尺按如图所示的方式叠放在一起,在图中标记的角中,所有与互余的角一共有个
15. 将直尺与三角尺按如图所示的方式叠放在一起,在图中标记的角中,所有与互余的角一共有个 16. 小明沿一段笔直的人行道行走,边走边欣赏风景,在由走到的过程中,通过隔离带的空隙 , 刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图, , 相邻两平行线间的距离相等, , 相交于 , 垂足为已知米请根据上述信息求标语的长度 .
16. 小明沿一段笔直的人行道行走,边走边欣赏风景,在由走到的过程中,通过隔离带的空隙 , 刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图, , 相邻两平行线间的距离相等, , 相交于 , 垂足为已知米请根据上述信息求标语的长度 . 17. 如图,在中,是边上的高,平分交于点 , , , 的面积等于 .
17. 如图,在中,是边上的高,平分交于点 , , , 的面积等于 . 18. 在一条笔直的航道上依次有甲、乙、丙三个港口,一艘船从甲港出发,沿直线匀速行驶经过乙港驶向丙港,最终到达丙港,设行驶后,与乙港的距离为 , 与的关系如图所示,下列结论:
18. 在一条笔直的航道上依次有甲、乙、丙三个港口,一艘船从甲港出发,沿直线匀速行驶经过乙港驶向丙港,最终到达丙港,设行驶后,与乙港的距离为 , 与的关系如图所示,下列结论:
甲港与丙港的距离是;
船在中途休息了;
船的行驶速度是;
的值为 .
其中正确的只填序号
三、计算题(本大题共1小题,共8.0分)
-
19. 某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证元,只限本人当年使用,凭证游泳每次再付费元;方式二:不购买会员证,每次游泳付费元.设小聪计划今年夏季游泳次数为为正整数 .(1)、根据题意,填写下表:
游泳次数
方式一的总费用元
方式二的总费用元
(2)、若小聪计划今年夏季游泳的总费用为元,通过计算说明选择哪种付费方式,她游泳的次数比较多?(3)、张老师是游泳爱好者,他计划今年夏季在这个游泳馆至少游泳次,通过计算说明,张老师选择哪种方式合算?四、解答题(本大题共7小题,共58.0分。解答应写出文字说明,证明过程或演算步骤)
-
20. 计算:(1)、;(2)、 .21. 先化简,再求值: , 其中 , .22. 如图,两条公路和相交于点,在的内部有工厂和 , 现要在内部修建一个货站 , 使货站到两条公路、的距离相等,且到两工厂、的距离相等,用尺规作出货站的位置.要求:不写作法,保留作图痕迹,写出结论
 23. 在一个不透明的盒子里装有颜色不同的黑、白两种球共个,它们除颜色不同外,其余都相同,王颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率定于(1)、请估计摸到白球的概率将会接近;(2)、计算盒子里白、黑两种颜色的球各有多少个?(3)、如果要使摸到白球的概率为 , 需要往盒子里再放入多少个白球?24. 如图,点、、、在直线上、之间不能直接测量 , 点、在异侧,测得 , , .
23. 在一个不透明的盒子里装有颜色不同的黑、白两种球共个,它们除颜色不同外,其余都相同,王颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中搅匀,经过大量重复上述摸球的过程,发现摸到白球的频率定于(1)、请估计摸到白球的概率将会接近;(2)、计算盒子里白、黑两种颜色的球各有多少个?(3)、如果要使摸到白球的概率为 , 需要往盒子里再放入多少个白球?24. 如图,点、、、在直线上、之间不能直接测量 , 点、在异侧,测得 , , . (1)、求证:≌;(2)、若 , , 求的长度.25. 由于受“”特大暴雨灾害的影响,南方某镇受灾严重,广大党员干部闻“汛”而动,组建、两个团队冲锋在灾后重建的第一线,筑起一道靓丽风景线该镇有两段长度相等的河渠挖掘任务,分别交给、两个团队同时进行挖掘,如图是反映所挖据的路程与挖掘时间之间关系的部分图象,根据图中的信息回答下列问题:
(1)、求证:≌;(2)、若 , , 求的长度.25. 由于受“”特大暴雨灾害的影响,南方某镇受灾严重,广大党员干部闻“汛”而动,组建、两个团队冲锋在灾后重建的第一线,筑起一道靓丽风景线该镇有两段长度相等的河渠挖掘任务,分别交给、两个团队同时进行挖掘,如图是反映所挖据的路程与挖掘时间之间关系的部分图象,根据图中的信息回答下列问题:
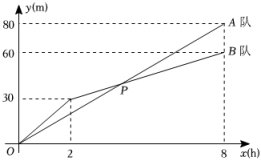 (1)、在挖掘过程中,队前个小时挖了 , 当挖掘个小时的时候,队比队多挖了;(2)、在这个小时内,队施工的平均速度是;(3)、开挖几小时后,队所挖掘的河渠长度开始超过队?(4)、你还能从图中得到什么信息写出一条即可26. 如图 , 已知正方形的边长为 , , , 点为正方形边上的动点,动点从点出发,沿着运动到点时停止,设点经过的路程为 , 的面积为 .
(1)、在挖掘过程中,队前个小时挖了 , 当挖掘个小时的时候,队比队多挖了;(2)、在这个小时内,队施工的平均速度是;(3)、开挖几小时后,队所挖掘的河渠长度开始超过队?(4)、你还能从图中得到什么信息写出一条即可26. 如图 , 已知正方形的边长为 , , , 点为正方形边上的动点,动点从点出发,沿着运动到点时停止,设点经过的路程为 , 的面积为 .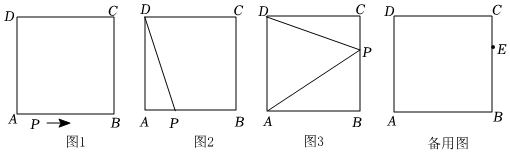 (1)、如图 , 当时,;(2)、如图 , 当点在边上运动时,;(3)、当时,求的值;(4)、若点是边上一点且 , 连接 , 在正方形的边上是否存在一点 , 使得与全等?若存在,求出此时的值;若不存在,请说明理由.
(1)、如图 , 当时,;(2)、如图 , 当点在边上运动时,;(3)、当时,求的值;(4)、若点是边上一点且 , 连接 , 在正方形的边上是否存在一点 , 使得与全等?若存在,求出此时的值;若不存在,请说明理由.
-