辽宁省丹东六中协作校联考2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共20.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在中国园林建筑中,洞窗是最生动的眼睛,主要以漏空图案填心为主,故也称镂空花窗花窗图案丰富多样,以各种植物,动物,字体,几何图案和其他图案为基础,相互交错形成多种吉祥图案则下列填心的图案中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在年发布的国际学术杂志上了解到,当前垂直型晶体管已经可以使芯片工艺级别达到 , 数据用科学记数法可表示为( )A、 B、 C、 D、3. 一个三角形的两边长分别为和 , 则第三边的长可能是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法中正确的是( )A、天宫六号货运飞船发射前各零件的检查是抽样调查 B、某小组有名同学,至少有名同学的生日在同一个月 C、可能性是的事件在一次试验中一定不会发生 D、为了解近十年宿迁初中生的视力变化趋势,采用扇形统计图最合适6. 若中,:::: , 则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、任意三角形7. 已知直线 , 将一块含角的直角三角板按如图所示方式放置,直角顶点在直线上,斜边与直线相交若 , 则的度数为( )
2. 在年发布的国际学术杂志上了解到,当前垂直型晶体管已经可以使芯片工艺级别达到 , 数据用科学记数法可表示为( )A、 B、 C、 D、3. 一个三角形的两边长分别为和 , 则第三边的长可能是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法中正确的是( )A、天宫六号货运飞船发射前各零件的检查是抽样调查 B、某小组有名同学,至少有名同学的生日在同一个月 C、可能性是的事件在一次试验中一定不会发生 D、为了解近十年宿迁初中生的视力变化趋势,采用扇形统计图最合适6. 若中,:::: , 则是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、任意三角形7. 已知直线 , 将一块含角的直角三角板按如图所示方式放置,直角顶点在直线上,斜边与直线相交若 , 则的度数为( ) A、 B、 C、 D、8. 如图,小明用一副三角板拼成一幅“帆船图”, , , , , 连结 , 则的度数是( )
A、 B、 C、 D、8. 如图,小明用一副三角板拼成一幅“帆船图”, , , , , 连结 , 则的度数是( ) A、 B、 C、 D、9. 老师在微信群发了这样一个图:以线段为边作正五边形和正三角形 , 连接 , 交于点 , 下列四位同学的说法不正确的是( )
A、 B、 C、 D、9. 老师在微信群发了这样一个图:以线段为边作正五边形和正三角形 , 连接 , 交于点 , 下列四位同学的说法不正确的是( )
甲
乙是的垂直平分线
丙是等腰三角形
丁与平行
A、甲 B、乙 C、丙 D、丁10. 小李和小陆从地出发,骑自行车沿同一条路行驶到地,小李先出发行驶后小陆出发,他们离出发地的距离和行驶时间之间的关系图象如图所示,根据图中的信息,有下列说法:
他们都行驶了;
小陆全程共用了;
小陆出发后 , 小陆和小李相遇;
小李在途中停留了;
其中正确的有( )
A、个 B、个 C、个 D、个二、填空题(本大题共8小题,共24.0分)
-
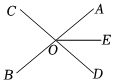
11. 如图,直线、相交于点 , 平分 , 若 , 则的度数是 .
 12. 现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,卡片除正面图案不同外,其余均相同,将三张卡片正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是。
12. 现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,卡片除正面图案不同外,其余均相同,将三张卡片正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是。 13. 学校七年级开展种植班树活动.已知一班的班树现在高80厘米,以后一年中每个月平均长高2厘米,x月后这棵树的高度为h厘米,则h与x的函数关系式为 .14. 已知是完全平方式,则的值是 .15. 如图,在中, , 平分 , 若 , , 则 .
13. 学校七年级开展种植班树活动.已知一班的班树现在高80厘米,以后一年中每个月平均长高2厘米,x月后这棵树的高度为h厘米,则h与x的函数关系式为 .14. 已知是完全平方式,则的值是 .15. 如图,在中, , 平分 , 若 , , 则 . 16. 小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠B=°.
16. 小丽从一张等腰三角形纸片ABC(AB=AC)中恰好剪出五个如图所示的小等腰三角形,其中BC=BD,EC=EF=FG=DG=DA,则∠B=°. 17. 如图,分别以 , , , 为边长作正方形,已知且满足 , .
17. 如图,分别以 , , , 为边长作正方形,已知且满足 , . (1)、若 , , 则图阴影部分的面积是;(2)、若图阴影部分的面积为 , 图四边形的面积为 , 则图阴影部分的面积是 .18. 如图,在中, , 点是上一点,交延长线于点 , 连接 , 若图中两阴影三角形的面积之差为即, , 则 .
(1)、若 , , 则图阴影部分的面积是;(2)、若图阴影部分的面积为 , 图四边形的面积为 , 则图阴影部分的面积是 .18. 如图,在中, , 点是上一点,交延长线于点 , 连接 , 若图中两阴影三角形的面积之差为即, , 则 .
三、解答题(本大题共8小题,共76.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算:(1)、;(2)、简便运算;(3)、;(4)、 .20. 先化简,再求值: , 其中 , .21. 在图示的正方形网格纸中,每个小正方形的边长都是 , 的三个顶点都在小正方形的顶点处,直线与网格中竖直的线相重合.

⑴直接写出的面积;
⑵作出关于直线对称的;
⑶在网格内找一点 , 使点到线段 , 的距离相等且在网格上直接标出点的位置,不写作法
22. 在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球其中红球个,白球个,黑球若干个,若从中任意摸出一个白球的概率是 .(1)、求盒子中黑球的个数;(2)、求任意摸出一个球是黑球的概率;(3)、能否通过只改变盒子中白球的数量,使得任意摸出一个球是红球的概率为 , 若能,请写出如何调整白球数量;若不能,请说明理由.23. 已知 , , , 试说明: .
请完善下面解答过程,并填写理由.
解:已知 ,
▲ ( ),
▲ 两直线平行,内错角相等 ,
已知 ,
▲ ( ),
同位角相等,两直线平行 ,
( ),
即 ,
已知 ,
等量代换 ,
即 ,
▲ ( ).
24. 如图,在中,为上一点,为中点,连接并延长至点使得 , 连 . (1)、求证:;(2)、连接 , 若 , 平分 , 平分 , 求的度数.
(1)、求证:;(2)、连接 , 若 , 平分 , 平分 , 求的度数.