辽宁省丹东市东港市2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本通共10个小题,每小题2分,共20分.在每小题给出的四个选项中,只有一项符合题目要求)
-
1. 以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 下列不等式一定成立的是( )A、 B、 C、 D、3. 当时,对于分式的说法正确的是( )A、分式的值为0 B、分式的值为 C、分式无意义 D、分式有意义4. 不等式组的解集为 , 则的值为( )A、-6 B、6 C、-2 D、25. 如图,的对角线 , 交于点O , 且 , , 若的周长为12,则的周长为( )
2. 若 , 下列不等式一定成立的是( )A、 B、 C、 D、3. 当时,对于分式的说法正确的是( )A、分式的值为0 B、分式的值为 C、分式无意义 D、分式有意义4. 不等式组的解集为 , 则的值为( )A、-6 B、6 C、-2 D、25. 如图,的对角线 , 交于点O , 且 , , 若的周长为12,则的周长为( ) A、10 B、12 C、15 D、206. 如图,在平面直角坐标系中,点的坐标是 , 将线段向右平移5个单位长度,得到线段 , 则点的对应点的坐标为( )
A、10 B、12 C、15 D、206. 如图,在平面直角坐标系中,点的坐标是 , 将线段向右平移5个单位长度,得到线段 , 则点的对应点的坐标为( ) A、 B、 C、 D、7. 如图,直线与直线相交于点 , 直线过点 , 则关于的不等式的解集为( )
A、 B、 C、 D、7. 如图,直线与直线相交于点 , 直线过点 , 则关于的不等式的解集为( ) A、 B、 C、 D、8. 如图,平分 , , , , , 则的长为( )
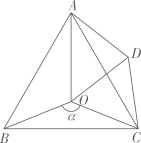
A、 B、 C、 D、8. 如图,平分 , , , , , 则的长为( ) A、13 B、12 C、11 D、109. 已知是三角形的三边,且满足则的形状为( )A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形10. 如图,在Rt中, , , 点O是边的中点,点 , 分别在边上,且 . 则下列结论中:①图中有两对全等的三角形;②;③若四边形的面积为2,则的面积为4;④ , 正确的结论有( )
A、13 B、12 C、11 D、109. 已知是三角形的三边,且满足则的形状为( )A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形10. 如图,在Rt中, , , 点O是边的中点,点 , 分别在边上,且 . 则下列结论中:①图中有两对全等的三角形;②;③若四边形的面积为2,则的面积为4;④ , 正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(本题共8个小题,每小题2分,共16分)
-
11. 因式分解: .12. 若关于的方程有增根,则的值是 .13. 如果一个多边形的每个外角都等于相邻内角的 , 则这个多边形的边数为 .14. 若多项式是一个完全平方式,则的值为 .15. 如图,在中,平分 , 于点 , 连接 , 若的面积为 , 的面积为 , 则的面积为 .
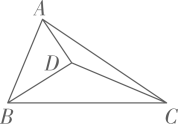 16. 如图,的对角线 , 相交于点 , 平分交于点 , 且 , , 连接 , 若 , 则的面积为 .
16. 如图,的对角线 , 相交于点 , 平分交于点 , 且 , , 连接 , 若 , 则的面积为 . 17. 在Rt中, , , 点在线段上, , 将线段绕点顺时针旋转得到线段于点 , 则的长为 .
17. 在Rt中, , , 点在线段上, , 将线段绕点顺时针旋转得到线段于点 , 则的长为 .
 18. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 点在轴的正半轴上,且 , 在平面直角坐标系内确定点 , 使得以点为顶点的四边形是平行四边形,则点的坐标为 .
18. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 点在轴的正半轴上,且 , 在平面直角坐标系内确定点 , 使得以点为顶点的四边形是平行四边形,则点的坐标为 .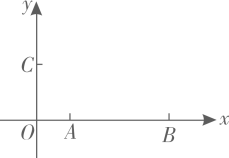
三、计算题(第19髟每小题5分,第20题5分,共15分)
-
19.(1)、解不等式组:(2)、分解因式:20. 先化简,再求值: , 其中 .
四、(第21题6分,第22题7分,共13分)
-
21. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .

⑴若将经过一次平移后得到对应图形 , 点的坐标为 , 请画出平移后的 , 并直接写出上的点的对应点的坐标(用含的代数式表示);
⑵直接写出(1)中经过一次平移得到的平移距离;
⑶在平面直角坐标系中画出关于原点O成中心对称的图形 .
22. 如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.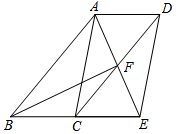 (1)、求证:BE=CD;(2)、若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
(1)、求证:BE=CD;(2)、若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.五、解答题:(第23题8分,第24题8分,共16分)
-
23. 甲、乙两同学的家与某科技馆的距离均为4000米,甲、乙两人同时从家出发去科技馆,甲同学先步行800米,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5分钟.求甲步行的速度.24. 某超市需购进一批圆珠笔,现有甲、乙两个批发商有相同品牌的圆珠笔可供选择,甲批发商每支圆珠笔都是1.8元;乙批发商圆珠笔售价如下表.设购买圆珠笔支,到两个批发商购买所需费用分别为、元.
购买圆珠笔数量 销售单价
不超过1000支时
2元/支
超过1000支部分
1.6元/支
(1)、如果要购买800支圆珠笔,若全部都在甲批发商处购买,所需费用为元;若全部都在乙批发商处购买,所需费用为元;(2)、当时,请分别求出、与之间的函数关系式;(3)、求该超市购买圆珠笔超过1000支时,选择哪一个批发商购买更合算.六、(第25题8分)