辽宁省阜新市2023年中考数学试卷
试卷更新日期:2023-09-01 类型:中考真卷
一、选择题(本题共10小题,每小题3分,共30分,在每一个小题给出的四个选中,只有一个是正确的)
-
1. 的相反数是( )A、2 B、 C、 D、2. 如图所示的几何体是由5个大小相同的立方块搭成的,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 在下列计算中,正确的是( )A、 B、 C、 D、4. 某中学甲、乙两支国旗护卫队的队员身高(单位:)数据如下:
3. 在下列计算中,正确的是( )A、 B、 C、 D、4. 某中学甲、乙两支国旗护卫队的队员身高(单位:)数据如下:甲队:178,177,179,179,178,178,177,178,177,179;
乙队:178,177,177,176,178,175,177,181,180,181.
若要判断哪支护卫队队员身高更为整齐,应该比较两组数据的( )
A、平均数 B、众数 C、中位数 D、方差5. 某中学举办“传承红色精神,讲好阜新故事”演讲比赛,共设置“海州矿精神”“三沟精神”“治沙精神”三个主题,每位选手随机选取一个主题参赛.如果小明和小宇都参加比赛,他们同时选中主题“海州矿精神”的概率是( )A、 B、 C、 D、6. 不等式的解集是( )A、 B、 C、 D、7. 如图,A , B , C是上的三点,若 , 则的度数是( ) A、 B、 C、 D、8. 近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商纷纷开展降价促销活动.某款燃油汽车今年3月份售价为23万元,5月份售价为16万元.设该款汽车这两月售价的月均下降率是x , 则所列方程正确的是( )A、 B、 C、 D、9. 如图,二次函数的图象与x轴的一个交点为 , 对称轴是直线 , 下列结论正确的是( )
A、 B、 C、 D、8. 近年来,由于新能源汽车的崛起,燃油汽车的销量出现了不同程度的下滑,经销商纷纷开展降价促销活动.某款燃油汽车今年3月份售价为23万元,5月份售价为16万元.设该款汽车这两月售价的月均下降率是x , 则所列方程正确的是( )A、 B、 C、 D、9. 如图,二次函数的图象与x轴的一个交点为 , 对称轴是直线 , 下列结论正确的是( )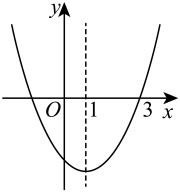 A、 B、 C、 D、点在函数图象上10. 如图,四边形是正方形,曲线叫作“正方形的渐开线”,其中 , , , , …的圆心依次按O , A , B,循环.当时,点的坐标是( )
A、 B、 C、 D、点在函数图象上10. 如图,四边形是正方形,曲线叫作“正方形的渐开线”,其中 , , , , …的圆心依次按O , A , B,循环.当时,点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共6个小题,每小题3分,共18分)
-
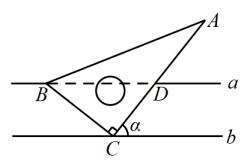
11. 计算: .12. 将一个三角尺按如图所示的位置摆放,直线 , 若 , 则的度数是 .
 13.
13.如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为
 14. 正比例函数的图象与反比例函数的图象相交于A , B两点,过点A作轴,垂足为点C , 连接 , 则的面积是 .15. 如图,在矩形中, . 连接 , 在和上分别截取 , 使 . 分别以点E和点F为圆心,以大于的长为半径作弧,两弧交于点G . 作射线交于点H , 则线段的长是 .
14. 正比例函数的图象与反比例函数的图象相交于A , B两点,过点A作轴,垂足为点C , 连接 , 则的面积是 .15. 如图,在矩形中, . 连接 , 在和上分别截取 , 使 . 分别以点E和点F为圆心,以大于的长为半径作弧,两弧交于点G . 作射线交于点H , 则线段的长是 . 16. 德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称.今年5月在此举办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加.甲、乙两名选手同时参加了往返(单程)的业余组比赛,如果全程保持匀速,甲、乙之间的距离s()与甲所用的时间(h)之间的函数关系如图所示,那么当甲到达终点时,乙距离终点 .
16. 德力格尔草原位于彰武县境内,以草场资源丰富,景色优美著称.今年5月在此举办的“漠上草原欢乐跑”首届马拉松比赛,吸引了千余名国内外选手参加.甲、乙两名选手同时参加了往返(单程)的业余组比赛,如果全程保持匀速,甲、乙之间的距离s()与甲所用的时间(h)之间的函数关系如图所示,那么当甲到达终点时,乙距离终点 .
三、解答题(本题共8个小题,17、18题每题6分,19、20题每题8分,21、22题每题10分,23、24题每题12分,共72分)
-
17. 先化简,再求值: , 其中 .18. 某中学数学兴趣小组的同学们,对函数(a , b , c是常数,)的性质进行了初步探究,部分过程如下,请你将其补充完整.
 (1)、当 , 时,即 , 当时,函数化简为;当时,函数化简为 .(2)、当 , , 时,即 .
(1)、当 , 时,即 , 当时,函数化简为;当时,函数化简为 .(2)、当 , , 时,即 .①该函数自变量x和函数值y的若干组对应值如下表:
…
-2 -1 0
1
2
3
4
…
…
6 m 2
0
2
4
6
…
其中 ▲ .
②在图1所示的平面直角坐标系内画出函数的图象.
(3)、当时,即 .①当时,函数化简为 ▲ .
②在图2所示的平面直角坐标系内画出函数的图象.
(4)、请写出函数(a , b , c是常数,)的一条性质: . (若所列性质多于一条,则仅以第一条为准)19. 如图,是的直径,点C , D是上异侧的两点, , 交的延长线于点E , 且平分 . (1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积.20. 端午节是中华民族的传统节日,节日里吃粽子是传统习俗.为了了解附近居民对A(肉粽子),B(蛋黄粽子).C(红枣粽子),D(葡萄干粽子)四种口味粽子的喜爱情况,某商场随机抽取了某小区的部分居民进行问卷调查(每人只能选一种口味),并将调查结果绘制成如下两幅不完整的统计图.
(1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积.20. 端午节是中华民族的传统节日,节日里吃粽子是传统习俗.为了了解附近居民对A(肉粽子),B(蛋黄粽子).C(红枣粽子),D(葡萄干粽子)四种口味粽子的喜爱情况,某商场随机抽取了某小区的部分居民进行问卷调查(每人只能选一种口味),并将调查结果绘制成如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)、参加此次问卷调查的居民共有人.(2)、通过计算将条形统计图补充完整.(3)、若该小区共有2000名居民,请估计喜爱A(肉粽子)的居民约有多少人.21. 如图,小颖家所在居民楼高为 , 从楼顶A处测得另一座大厦顶部C的仰角是 , 而大厦底部D的俯角是 . (1)、求两楼之间的距离 .(2)、求大厦的高度 .
(1)、求两楼之间的距离 .(2)、求大厦的高度 .(结果精确到 . 参考数据: , , )
22. 为了进一步丰富校园文体活动,某中学准备一次性购买若干个足球和排球,用480元购买足球的数量和用390元购买排球的数量相同,已知足球的单价比排球的单价多15元.(1)、求:足球和排球的单价各是多少元?(2)、根据学校实际情况,需一次性购买足球和排球共100个,但要求其总费用不超过7550元,那么学校最多可以购买多少个足球?23. 如图,在正方形中,线段绕点C逆时针旋转到处,旋转角为 , 点F在直线上,且 , 连接 . (1)、如图1,当时,
(1)、如图1,当时,①求的大小(用含的式子表示).
②求证: .
(2)、如图2,取线段的中点G , 连接 , 已知 , 请直接写出在线段旋转过程中()面积的最大值.24. 如图,在平面直角坐标系中,二次函数的图象与轴交于点和点 , 与y轴交于点C . (1)、求这个二次函数的表达式.(2)、如图1,二次函数图象的对称轴与直线交于点D , 若点M是直线上方抛物线上的一个动点,求面积的最大值.(3)、如图2,点是直线上的一个动点,过点的直线与平行,则在直线上是否存在点 , 使点与点关于直线对称?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求这个二次函数的表达式.(2)、如图1,二次函数图象的对称轴与直线交于点D , 若点M是直线上方抛物线上的一个动点,求面积的最大值.(3)、如图2,点是直线上的一个动点,过点的直线与平行,则在直线上是否存在点 , 使点与点关于直线对称?若存在,请直接写出点的坐标;若不存在,请说明理由.