黑龙江省哈尔滨市2023年中考数学试卷
试卷更新日期:2023-09-01 类型:中考真卷
一、选择题(每小题3分,共计30分)
-
1. 的绝对值是( )A、 B、10 C、 D、2. 下列运算一定正确的是( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
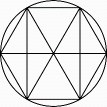 B、
B、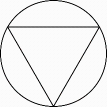 C、
C、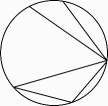 D、
D、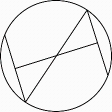 4. 七个大小相同的正方体搭成的几何体如图所示,其俯视图是( )
4. 七个大小相同的正方体搭成的几何体如图所示,其俯视图是( )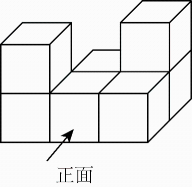 A、
A、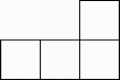 B、
B、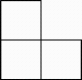 C、
C、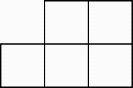 D、
D、 5. 如图,是的切线,A为切点,连接﹐点C在上, , 连接并延长,交于点D , 连接 . 若 , 则的度数为( )
5. 如图,是的切线,A为切点,连接﹐点C在上, , 连接并延长,交于点D , 连接 . 若 , 则的度数为( )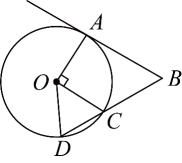 A、 B、 C、 D、6. 方程的解为( )A、 B、 C、 D、7. 为了改善居民生活环境,云中小区对一块矩形空地进行绿化,这块空地的长比宽多6米,面积为720平方米,设矩形空地的长为x米,根据题意,所列方程正确的是( )A、 B、 C、 D、8. 将枚黑棋子5枚白棋子装入一个不透明的空盒子里,这些棋子除颜色外无其他差别,从盒子中随机取出一枚棋子,则取出的棋子是黑棋子的概率是( )A、 B、 C、 D、9. 如图, , 相交于点 , , 是的中点, , 交于点 . 若 , 则的长为( )
A、 B、 C、 D、6. 方程的解为( )A、 B、 C、 D、7. 为了改善居民生活环境,云中小区对一块矩形空地进行绿化,这块空地的长比宽多6米,面积为720平方米,设矩形空地的长为x米,根据题意,所列方程正确的是( )A、 B、 C、 D、8. 将枚黑棋子5枚白棋子装入一个不透明的空盒子里,这些棋子除颜色外无其他差别,从盒子中随机取出一枚棋子,则取出的棋子是黑棋子的概率是( )A、 B、 C、 D、9. 如图, , 相交于点 , , 是的中点, , 交于点 . 若 , 则的长为( ) A、2 B、4 C、6 D、810. 一条小船沿直线从码头向码头匀速前进,到达码头后,停留一段时间,然后原路匀速返回码头.在整个过程中,这条小船与码头的距离s(单位:)与所用时间(单位:)之间的关系如图所示,则这条小船从码头到码头的速度和从码头返回码头的速度分别为( )
A、2 B、4 C、6 D、810. 一条小船沿直线从码头向码头匀速前进,到达码头后,停留一段时间,然后原路匀速返回码头.在整个过程中,这条小船与码头的距离s(单位:)与所用时间(单位:)之间的关系如图所示,则这条小船从码头到码头的速度和从码头返回码头的速度分别为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共计30分)
-
11. 船闸是我国劳动人民智慧的结晶,三峡船闸的“人”字闸门是目前世界上最大的巨型闸门,重867000千克,用科学记数法表示为千克.12. 在函数中,自变量x的取值范围是 .13. 已知反比例函数的图象经过点 , 则a的值为 .14. 计算的结果是 .15. 把多项式分解因式的结果是 .16. 抛物线与y轴的交点坐标 .17. 不等式组的解集是 .18. 一个扇形的圆心角是 , 弧长是 , 则扇形的半径是cm.19. 矩形的对角线 , 相交于点 , 点在矩形边上,连接 . 若 , , 则 .20. 如图在正方形中,点E在上,连接 , , F为的中点连接 . 若 , 则的长为 .

三、解答题(共60分)
-
21. 先化简,再求代数式的值,其中 .22. 如图,方格纸中每个小正方形的边长均为个单位长度,线段和线段的端点均在小正方形的顶点上.
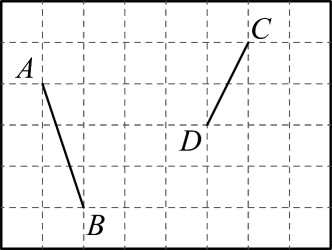 (1)、在方格纸中画出 , 且为钝角(点在小正方形的顶点上);(2)、在方格纸中将线段向下平移个单位长度,再向右平移个单位长度后得到线段(点的对应点是点 , 点的对应点是点),连接 , 请直接写出线段的长.23. 军乐中学开展以“我最喜欢的劳动实践课”为主题的调查活动,围绕“在园艺课,泥塑课,编织课、烹饪课四门劳动实践课中,你最喜欢哪一门课?(必选且只选一门)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢泥塑课的学生人数占所调查人数的 .
(1)、在方格纸中画出 , 且为钝角(点在小正方形的顶点上);(2)、在方格纸中将线段向下平移个单位长度,再向右平移个单位长度后得到线段(点的对应点是点 , 点的对应点是点),连接 , 请直接写出线段的长.23. 军乐中学开展以“我最喜欢的劳动实践课”为主题的调查活动,围绕“在园艺课,泥塑课,编织课、烹饪课四门劳动实践课中,你最喜欢哪一门课?(必选且只选一门)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢泥塑课的学生人数占所调查人数的 .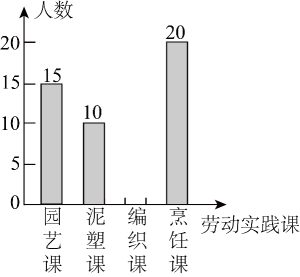
请你根据图中提供的信息解答下列问题:
(1)、在这次调查中,一共抽取了多少名学生?(2)、请通过计算补全条形统计图;(3)、若军乐中学共有1200名学生,请你估计该中学最喜欢烹任课的学生共有多少名.24. 已知四边形是平行四边形,点在对角线上,点在边上,连接 , , .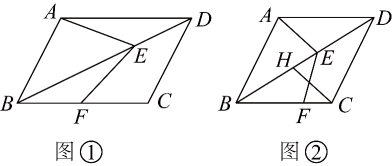 (1)、如图①,求证;(2)、如图②,若 , 过点作交于点 , 在不添加任何辅助线的情况下,请直接写出图②中四个角(除外),使写出的每个角都与相等.25. 佳衣服装厂给某中学用同样的布料生产 , 两种不同款式的服装,每套款服装所用布料的米数相同,每套款服装所用布料的米数相同,若套款服装和套款服装需用布料米,套款服装和套款服装需用布料米.(1)、求每套款服装和每套款服装需用布料各多少米;(2)、该中学需要 , 两款服装共套,所用布料不超过米,那么该服装厂最少需要生产多少套款服装?26. 已知内接于 , 为的直径,N为的中点,连接交于点H .
(1)、如图①,求证;(2)、如图②,若 , 过点作交于点 , 在不添加任何辅助线的情况下,请直接写出图②中四个角(除外),使写出的每个角都与相等.25. 佳衣服装厂给某中学用同样的布料生产 , 两种不同款式的服装,每套款服装所用布料的米数相同,每套款服装所用布料的米数相同,若套款服装和套款服装需用布料米,套款服装和套款服装需用布料米.(1)、求每套款服装和每套款服装需用布料各多少米;(2)、该中学需要 , 两款服装共套,所用布料不超过米,那么该服装厂最少需要生产多少套款服装?26. 已知内接于 , 为的直径,N为的中点,连接交于点H .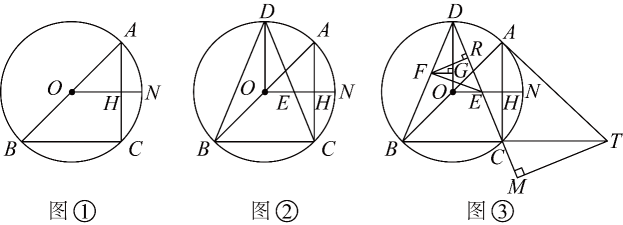 (1)、如图①,求证;(2)、如图②,点D在上,连接 , , , 交于点E , 若 , 求证;(3)、如图③,在(2)的条件下,点F在上,过点F作 , 交于点G . , 过点F作 , 垂足为R , 连接 , , , 点T在的延长线上,连接 , 过点T作 , 交的延长线于点M , 若 , 求的长.27. 在平面直角坐标系中,为坐标原点,抛物线与轴交于点 , , 与轴交于点 .
(1)、如图①,求证;(2)、如图②,点D在上,连接 , , , 交于点E , 若 , 求证;(3)、如图③,在(2)的条件下,点F在上,过点F作 , 交于点G . , 过点F作 , 垂足为R , 连接 , , , 点T在的延长线上,连接 , 过点T作 , 交的延长线于点M , 若 , 求的长.27. 在平面直角坐标系中,为坐标原点,抛物线与轴交于点 , , 与轴交于点 .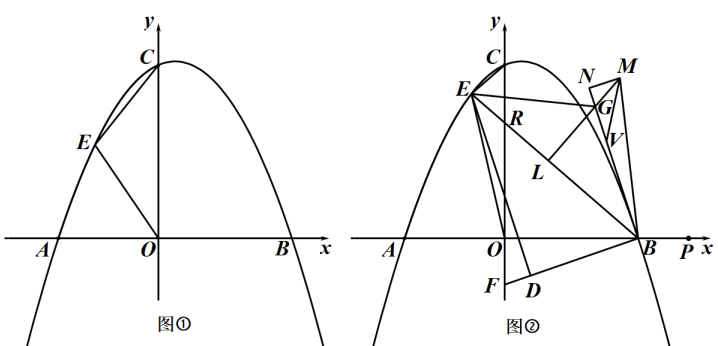 (1)、求 , 的值;(2)、如图①,是第二象限抛物线上的一个动点,连接 , , 设点的横坐标为 , 的面积为 , 求关于的函数解析式(不要求写出自变量的取值范围);(3)、如图②,在(2)的条件下,当时,连接交轴于点 , 点在轴负半轴上,连接 , 点在上,连接 , 点在线段上(点不与点重合),过点作的垂线与过点且平行于的直线交于点 , 为的延长线上一点,连接 , , 使 , 是轴上一点,且在点的右侧, , 过点作 , 交的延长线于点 , 点在上,连接 , 使 , 若 , 求直线的解析式.
(1)、求 , 的值;(2)、如图①,是第二象限抛物线上的一个动点,连接 , , 设点的横坐标为 , 的面积为 , 求关于的函数解析式(不要求写出自变量的取值范围);(3)、如图②,在(2)的条件下,当时,连接交轴于点 , 点在轴负半轴上,连接 , 点在上,连接 , 点在线段上(点不与点重合),过点作的垂线与过点且平行于的直线交于点 , 为的延长线上一点,连接 , , 使 , 是轴上一点,且在点的右侧, , 过点作 , 交的延长线于点 , 点在上,连接 , 使 , 若 , 求直线的解析式.