黑龙江省牡丹江市海宁市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(每小题3分,满分30分)
-
1. 下列二次根式中是最简二次根式的是( )A、 B、 C、 D、2. 为庆祝神舟十六号载人飞船发射成功,学校开展航天知识竞赛活动,经过几轮筛选,本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学的平均数(单位:分)及方差(单位:分2)如表所示,如果要选择一名成绩好且状态稳定的同学参赛,那么应该选择( )
甲
乙
丙
丁
平均数
96
98
95
98
方差
2
0.4
0.4
1.6
A、甲 B、乙 C、丙 D、丁3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,均匀地向此容器内注水,直到把容器注满,在注水过程中,下列图象能大致反映水面高度h随注水时间t变化规律的是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,在平面直角坐标系中,四边形是正方形,点的坐标是 , 点为边上一点, , 沿折叠正方形,折叠后点落在平面内点处,则点的坐标为( )
5. 如图,在平面直角坐标系中,四边形是正方形,点的坐标是 , 点为边上一点, , 沿折叠正方形,折叠后点落在平面内点处,则点的坐标为( ) A、 B、 C、 D、6. 下列说法:①四边相等的四边形一定是菱形;②顺次连接矩形各边中点形成的四边形一定是正方形:③对角线相等的四边形一定是矩形;④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分.其中正确的有( )A、4个 B、3个 C、2个 D、1个7. 李老师参加本校青年数学教师优质课比赛,笔试得90分,微型课得92分,教学反思得88分.按照如图所显示的笔试、微型课、教学反思的权重,李老师的综合成绩为( )
A、 B、 C、 D、6. 下列说法:①四边相等的四边形一定是菱形;②顺次连接矩形各边中点形成的四边形一定是正方形:③对角线相等的四边形一定是矩形;④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分.其中正确的有( )A、4个 B、3个 C、2个 D、1个7. 李老师参加本校青年数学教师优质课比赛,笔试得90分,微型课得92分,教学反思得88分.按照如图所显示的笔试、微型课、教学反思的权重,李老师的综合成绩为( ) A、88分 B、90分 C、91分 D、92分8. 直线和的图象可能是( )A、
A、88分 B、90分 C、91分 D、92分8. 直线和的图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,菱形中,对角线相交于点 , 过点作于点 , 连接 , 若 , 则菱形的面积为( )
9. 如图,菱形中,对角线相交于点 , 过点作于点 , 连接 , 若 , 则菱形的面积为( ) A、12 B、24 C、48 D、10. 如图,已知在正方形外取一点 , 连接 . 过点作的垂线交于点 . 若 . 下列结论:①;②;③点到直线的距离为;④;⑤;其中正确结论的序号有( )
A、12 B、24 C、48 D、10. 如图,已知在正方形外取一点 , 连接 . 过点作的垂线交于点 . 若 . 下列结论:①;②;③点到直线的距离为;④;⑤;其中正确结论的序号有( ) A、①③④ B、①②④ C、③④⑤ D、①③⑤
A、①③④ B、①②④ C、③④⑤ D、①③⑤二、填空题(每小题3分,满分30分)
-
11. 在函数中,自变量的取值范围是 .12. 如图,在中,点是的中点,点分别在线段及其延长线上,且 , 请你添加一个条件 , 使四边形是菱形
 13. 已知一组数据有唯一众数,那么这组数据的中位数是 .14. 若一次函数的图不经过第二象限,则的取值范围为 .15. 如图,在平行四边形中,点分别是的中点, , 垂足为 , 与交于点 , 若 , 则的长为 .
13. 已知一组数据有唯一众数,那么这组数据的中位数是 .14. 若一次函数的图不经过第二象限,则的取值范围为 .15. 如图,在平行四边形中,点分别是的中点, , 垂足为 , 与交于点 , 若 , 则的长为 . 16. 下列对于一次函数的说法,正确的有(填写序号)
16. 下列对于一次函数的说法,正确的有(填写序号)①图象经过二、三、四象限;
②图象与两坐标轴围成的面积是6;
③随的增大而减小;
④当时,;
⑤当时, .
17. 如图,在矩形中,对角线相交于点的平分线交于点 , 若 , 则 . 18. 如图,在平面直角坐标系中,直线与直线相交于 , 则关于的不等式的解集是 .
18. 如图,在平面直角坐标系中,直线与直线相交于 , 则关于的不等式的解集是 .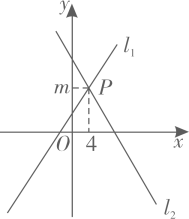 19. 已知在矩形中, , 点在边上, , 点在矩形的边上,是等腰三角形,则的底边长为 .20. 在正方形按如图的方式放置,点和点分别在直线和轴上,则点的坐标是(为正整数).
19. 已知在矩形中, , 点在边上, , 点在矩形的边上,是等腰三角形,则的底边长为 .20. 在正方形按如图的方式放置,点和点分别在直线和轴上,则点的坐标是(为正整数).
三、解答题(满分60分)
-
21. 计算(1)、(2)、22. 甲、乙两校参加市教育局举办的学生英语口语竞赛,两校参赛人数相等,比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.

甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
8
(1)、在图①中,“7分”所在扇形的圆心角等于 .(2)、请你将图②的统计图补充完整.(3)、经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好?(4)、如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?23. 如图,点是平行四边形中边的中点,连接并延长交的延长线于点 , 连接 (1)、求证:四边形是矩形;(2)、若是边长为4的等边三角形,求四边形的面积.24. 某商场准备购进A,B两种型号冰箱,每台A型号冰箱进价比每台B型号冰箱的进价多500元,用60000元购进A型号冰箱的数量与用45000元购进B型号冰箱的数量相同,请解答下列问题:(1)、A,B两种型号冰箱每台进价各是多少元?(2)、若每台A型号冰箱售价为2500元,每台B型号冰箱售价为1800元,商场决定同时购进A,B两种型号冰箱20台,且全部售出,请写出所获的利润y(元)与A型号冰箱x(台)的函数关系式,若商场用不超过36000元购进A,B两种型号冰箱,A型号冰箱至少购进10台,则有几种购买方案?(3)、在(2)的条件下,将不超过所获得的最大利润再次购买A,B两种型号冰箱捐赠给某个中学,请直接写出捐赠A,B型号冰箱总数最多是多少台?25. 甲、乙两车分别从A,B两地同时出发,匀速行驶,先相向而行.途中乙车因故停留1小时,然后以原速继续向A地行驶,甲车到达B地后,立即按原路原速返回A地(甲车掉头的时间忽略不计),到达A地后停止行驶,原地休息;甲、乙两车距B地的路程y(千米)与所用时间x(时)之间的函数图象如图,请结合图象信息解答下列问题:
(1)、求证:四边形是矩形;(2)、若是边长为4的等边三角形,求四边形的面积.24. 某商场准备购进A,B两种型号冰箱,每台A型号冰箱进价比每台B型号冰箱的进价多500元,用60000元购进A型号冰箱的数量与用45000元购进B型号冰箱的数量相同,请解答下列问题:(1)、A,B两种型号冰箱每台进价各是多少元?(2)、若每台A型号冰箱售价为2500元,每台B型号冰箱售价为1800元,商场决定同时购进A,B两种型号冰箱20台,且全部售出,请写出所获的利润y(元)与A型号冰箱x(台)的函数关系式,若商场用不超过36000元购进A,B两种型号冰箱,A型号冰箱至少购进10台,则有几种购买方案?(3)、在(2)的条件下,将不超过所获得的最大利润再次购买A,B两种型号冰箱捐赠给某个中学,请直接写出捐赠A,B型号冰箱总数最多是多少台?25. 甲、乙两车分别从A,B两地同时出发,匀速行驶,先相向而行.途中乙车因故停留1小时,然后以原速继续向A地行驶,甲车到达B地后,立即按原路原速返回A地(甲车掉头的时间忽略不计),到达A地后停止行驶,原地休息;甲、乙两车距B地的路程y(千米)与所用时间x(时)之间的函数图象如图,请结合图象信息解答下列问题: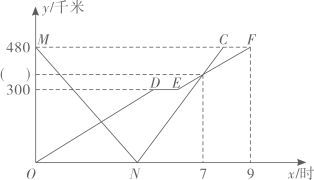 (1)、A,B两地的路程是千米,乙车的速度为千米/时,在图中的内填上正确的数.(2)、求甲车从B地返回A地的过程中,y与x的函数关系式(不需要写出自变量的取值范围).(3)、两车出发后几小时相距120千米,请直接写出答案.26. 在菱形中,对角线交于点 , 点是直线上一点,将线段绕点顺时针旋转到 , 连接 .
(1)、A,B两地的路程是千米,乙车的速度为千米/时,在图中的内填上正确的数.(2)、求甲车从B地返回A地的过程中,y与x的函数关系式(不需要写出自变量的取值范围).(3)、两车出发后几小时相距120千米,请直接写出答案.26. 在菱形中,对角线交于点 , 点是直线上一点,将线段绕点顺时针旋转到 , 连接 . (1)、当点在线段上时,如图①,求证: . (提示:连接 . )(2)、当点在线段延长线上时,如图②;当点在线段延长线上时,如图③,请直接写出线段的数量关系,不需要证明;(3)、在(1)、(2)的条件下,若 , 则 .
(1)、当点在线段上时,如图①,求证: . (提示:连接 . )(2)、当点在线段延长线上时,如图②;当点在线段延长线上时,如图③,请直接写出线段的数量关系,不需要证明;(3)、在(1)、(2)的条件下,若 , 则 .