黑龙江省佳木斯二十中、十三中、三中2022-2023学年七年级(下)期末数学试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列运算中,正确的是( )A、 B、 C、 D、2. 点所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、
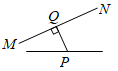 B、
B、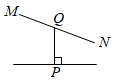 C、
C、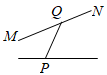 D、
D、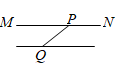 4. 若是关于 , 的二元一次方程,则的值为( )A、 B、 C、 D、5. 下列调查中,最适合采用全面调查的是( )A、了解全国中学生的睡眠时间 B、了解某河流的水质情况 C、调查全班同学的视力情况 D、了解一批灯泡的使用寿命6. 已知四个实数 , , , ,若 , ,则( )A、 B、 C、 D、7. 端午节前夕,某食品加工厂准备将生产的粽子装入A、B两种食品盒中,A种食品盒每盒装8个粽子,B种食品盒每盒装10个粽子,若现将200个粽子分别装入A、B两种食品盒中(两种食品盒均要使用并且装满),则不同的分装方式有( )A、2种 B、3种 C、4种 D、5种8. 关于的不等式组的整数解只有个,则的取值范围是( )A、 B、 C、 D、9. 如图,长方形中, , 现将这一长方形纸片沿折叠,当折痕与的夹角( )时, .
4. 若是关于 , 的二元一次方程,则的值为( )A、 B、 C、 D、5. 下列调查中,最适合采用全面调查的是( )A、了解全国中学生的睡眠时间 B、了解某河流的水质情况 C、调查全班同学的视力情况 D、了解一批灯泡的使用寿命6. 已知四个实数 , , , ,若 , ,则( )A、 B、 C、 D、7. 端午节前夕,某食品加工厂准备将生产的粽子装入A、B两种食品盒中,A种食品盒每盒装8个粽子,B种食品盒每盒装10个粽子,若现将200个粽子分别装入A、B两种食品盒中(两种食品盒均要使用并且装满),则不同的分装方式有( )A、2种 B、3种 C、4种 D、5种8. 关于的不等式组的整数解只有个,则的取值范围是( )A、 B、 C、 D、9. 如图,长方形中, , 现将这一长方形纸片沿折叠,当折痕与的夹角( )时, .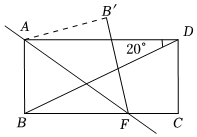 A、 B、 C、 D、10. 九章算术中有这样的问题:只闻隔壁人分银,不知多少银和人;每人两少两,每人半斤多半斤;试问各位善算者,多少人分多少银?注:这里的斤是指市斤,市斤两设共有人,两银子,下列方程组中正确的是( )A、 B、 C、 D、
A、 B、 C、 D、10. 九章算术中有这样的问题:只闻隔壁人分银,不知多少银和人;每人两少两,每人半斤多半斤;试问各位善算者,多少人分多少银?注:这里的斤是指市斤,市斤两设共有人,两银子,下列方程组中正确的是( )A、 B、 C、 D、二、填空题(本大题共7小题,共21.0分)
-
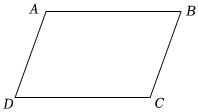
11. 如图,已知四边形 , 要使 , 添加的条件是 填一个即可 .
 12. 在平面直角坐标系中,将点向上平移个单位长度,再向左平移个单位长度得到的点的坐标是 .13. 已知的平方根是 , 则的立方根是 .14. 已知二元一次方程组 , 则的值为.15. 如图,已知直线与和分别相交于点和点 , 且 , , 则的度数是 .
12. 在平面直角坐标系中,将点向上平移个单位长度,再向左平移个单位长度得到的点的坐标是 .13. 已知的平方根是 , 则的立方根是 .14. 已知二元一次方程组 , 则的值为.15. 如图,已知直线与和分别相交于点和点 , 且 , , 则的度数是 .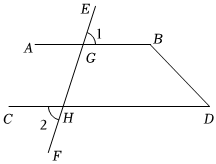 16. 我们定义一种新运算: , 如 , 则关于的不等式的最大整数解为 .17. 如图, , 的平分线交于点 , 是上的一点,的平分线交于点 , 且 , 下列结论:平分;;若 , 则;与互余的角有个,其中正确的有 把你认为正确结论的序号都填上
16. 我们定义一种新运算: , 如 , 则关于的不等式的最大整数解为 .17. 如图, , 的平分线交于点 , 是上的一点,的平分线交于点 , 且 , 下列结论:平分;;若 , 则;与互余的角有个,其中正确的有 把你认为正确结论的序号都填上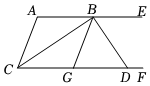
三、解答题(本大题共8小题,共69.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 计算: .19. 解方程组:(1)、;(2)、 .20. 解不等式组:(1)、;(2)、 .21. 为了解某校八年级学生立定跳远水平,随机抽取该年级名学生进行测试,并把测试成绩单位:绘制成了不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩频数分布表
分组
频数
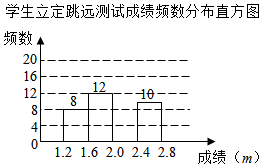
请根据频数分布所提供的信息,完成下列问题:
(1)、求表中 , 的值;(2)、请将下列频数分布直方图补充完整;(3)、该校八年级共有名学生,估计该年级立定跳远成绩在范围内的学生有多少人?22. 某网店“双”前准备从厂家选购甲、乙两种商品,乙种商品每件进价比甲种商品每件进价少元,若购进件甲种商品和件乙种商品共需要元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、若甲种商品的售价为每件元,乙种商品的售价为每件元,该网店准备购进甲、乙两种商品共件,且这两种商品全部售出后总利润不少于元,则乙种商品最多可购进多少件?23. 已知是平面直角坐标系中的一点,若 , 是关于 , 的二元一次方程组的解,则称为该方程组的“梦想点”例如:是二元一次方程组 , 的“梦想点”根据以上定义,回答下列问题:(1)、求关于 , 的二元一次方程组的“梦想点”.(2)、若关于 , 的方程组与的“梦想点”相同,求 , 的值.24. 已知 , 点为平面内一点,于 .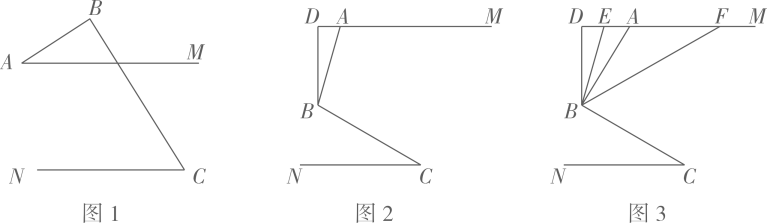 (1)、如图 , 直接写出和之间的数量关系;(2)、如图 , 过点作于点 , 求证:;(3)、如图 , 在问的条件下,点、在上,连接、、 , 平分 , 平分 , 若 , , 求的度数.25. 在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).
(1)、如图 , 直接写出和之间的数量关系;(2)、如图 , 过点作于点 , 求证:;(3)、如图 , 在问的条件下,点、在上,连接、、 , 平分 , 平分 , 若 , , 求的度数.25. 在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).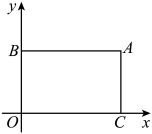 (1)、直接写出点B和点C的坐标.(2)、当点P运动时,用含t的式子表示线段AP的长,(3)、点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使 , 若存在,请求出t值,若不存在,请说明理由.
(1)、直接写出点B和点C的坐标.(2)、当点P运动时,用含t的式子表示线段AP的长,(3)、点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使 , 若存在,请求出t值,若不存在,请说明理由.