黑龙江省绥化市肇东市2022-2023学年八年级下学期7月期末数学试题
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下面的图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、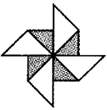 D、
D、 2. 下列关于的方程中,一定是一元二次方程的是( )A、 B、 C、 D、3. 若是二次函数,则的值是( )A、 B、3 C、9 D、4. 若抛物线先向左平移2个单位长度,再向下平移3个单位长度,则所得到的新拋物线的解析式时( )A、 B、 C、 D、5. 若是一元二次方程的一个实数根,则的值为( )A、2021 B、2020 C、2019 D、20186. 要组织一次篮球邀请赛,参赛的每个队之间都要比赛一场,计划安排20场比赛,设比赛组织者应邀请个队参赛,则满足的关系式为( )A、 B、 C、 D、7. 关于一元二次方程的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定根的情况8. 已知点 , 均在抛物线上,下列说法中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )A、
2. 下列关于的方程中,一定是一元二次方程的是( )A、 B、 C、 D、3. 若是二次函数,则的值是( )A、 B、3 C、9 D、4. 若抛物线先向左平移2个单位长度,再向下平移3个单位长度,则所得到的新拋物线的解析式时( )A、 B、 C、 D、5. 若是一元二次方程的一个实数根,则的值为( )A、2021 B、2020 C、2019 D、20186. 要组织一次篮球邀请赛,参赛的每个队之间都要比赛一场,计划安排20场比赛,设比赛组织者应邀请个队参赛,则满足的关系式为( )A、 B、 C、 D、7. 关于一元二次方程的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定根的情况8. 已知点 , 均在抛物线上,下列说法中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则9. 在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )A、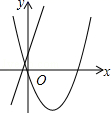 B、
B、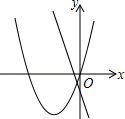 C、
C、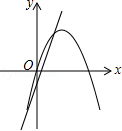 D、
D、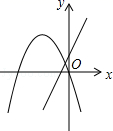 10. 方程经过配方法化为的形式,正确的是( )A、 B、 C、 D、
10. 方程经过配方法化为的形式,正确的是( )A、 B、 C、 D、二、填空题(每空3分,共30分)
-
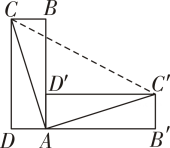
11. 点绕着原点逆时针方向旋转90°与点重合,则的坐标为 .12. 二次函数的顶点坐标是 .13. 如图,将矩形绕点顺时针旋转90°后,得到矩形 , 如果 , 那么 .
 14. 如图,二次函数的图象与轴相交于和两点,当函数值时,自变量的取值范围是 .
14. 如图,二次函数的图象与轴相交于和两点,当函数值时,自变量的取值范围是 .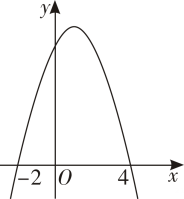 15. 如图是二次函数的图象,其对称轴为 , 下列结论:①;②;③;④若 , 是抛物线上两点,则其中结论正确的有 .
15. 如图是二次函数的图象,其对称轴为 , 下列结论:①;②;③;④若 , 是抛物线上两点,则其中结论正确的有 .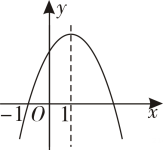 16. 三角形两边长分别是8和6,第三边的长是一元二次方程的一个实数根,则该三角形的面积是 .17. 如果二次函数的图象的顶点在轴上,那么 .18. 已知二次函数的部分图象如下图所示,则关于的一元二次方程的解为 .
16. 三角形两边长分别是8和6,第三边的长是一元二次方程的一个实数根,则该三角形的面积是 .17. 如果二次函数的图象的顶点在轴上,那么 .18. 已知二次函数的部分图象如下图所示,则关于的一元二次方程的解为 .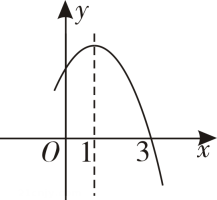 19. 某市某企业为节约用水,自建污水净化站.7月份净化污水6000吨,9月份增加到7260吨,则这两个月净化的污水量平均每月增长的百分率为 .20. 若关于的一元二次方程的一个根是 , 则另一个根是 .
19. 某市某企业为节约用水,自建污水净化站.7月份净化污水6000吨,9月份增加到7260吨,则这两个月净化的污水量平均每月增长的百分率为 .20. 若关于的一元二次方程的一个根是 , 则另一个根是 .三、解答题(共60分)
-
21. 解下列方程(1)、;(2)、;(3)、;(4)、 .22. 已知 , 是方程的两个根,求代数式的值.23. 如图,是正三角形内的一点,且 , , . 若将绕点逆时针旋转后,得到 .
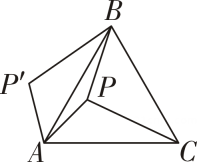 (1)、求点与点之间的距离;(2)、的度数.24. 已知关于的一元二次方程 ,(1)、求证:无论取何值,方程总有两个不相等的实数根;(2)、若方程有两个实数根 , , 且 , 求的值.25. 阅读并解答问题:用配方法可以解一元二次方程,还可以用它来解决很多问题.
(1)、求点与点之间的距离;(2)、的度数.24. 已知关于的一元二次方程 ,(1)、求证:无论取何值,方程总有两个不相等的实数根;(2)、若方程有两个实数根 , , 且 , 求的值.25. 阅读并解答问题:用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为 , 所以就有最小值1,
即 , 只有当时,才能得到这个式子的最小值1.
同样,因为 , 所以有最大值1,
即 , 只有在时,才能得到这个式子的最大值1.
(1)、当时,代数式有最(填写大或小)值为;(2)、矩形花园的一面靠墙,另外三面的棚栏所围成的总长度是 , 当花园与墙垂直的边长为多少时,花园的面积最大?最大面积是多少?
 26. 如图,二次函数的图象与轴交于和两点,交轴于点 , 点、是二次函数图象上的一对对称点,一次函数的图象过点、 .
26. 如图,二次函数的图象与轴交于和两点,交轴于点 , 点、是二次函数图象上的一对对称点,一次函数的图象过点、 . (1)、请直接写出点的坐标.(2)、求二次函数的解析式.(3)、根据图象直接写出使一次函数值大于二次函数值的的取值范围.27. 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第天生产的粽子数量为只,与满足下列关系式: .
(1)、请直接写出点的坐标.(2)、求二次函数的解析式.(3)、根据图象直接写出使一次函数值大于二次函数值的的取值范围.27. 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第天生产的粽子数量为只,与满足下列关系式: .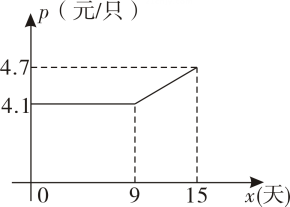 (1)、李明第几天生产的粽子数量为420只?(2)、如图,设第天每只粽子的成本是元,与之间的关系可用图中的函数图象来刻画.若李明第天创造的利润为元,求与之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
(1)、李明第几天生产的粽子数量为420只?(2)、如图,设第天每只粽子的成本是元,与之间的关系可用图中的函数图象来刻画.若李明第天创造的利润为元,求与之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)