黑龙江省哈尔滨市香坊区2022-2023学年（五四学制）六年级下学期期末数学试题

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. $- \frac{3}{2}$ 的相反数是 $($ $)$

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
2. 根据规划，中国倡导的“一带一路”地区覆盖总人口约为4400000000，请用科学记数法表示这个数为（）

A、 $44 \times 1 0^{8}$ B、 $4.4 \times 1 0^{9}$ C、 $4.4 \times 1 0^{8}$ D、 $4.4 \times 1 0^{10}$

查看试题解析
3. 下面运算一定正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $3 x + 2 x = 5 x^{2}$ C、 $2 x^{2} y - 2 y x^{2} = 0$ D、 $3 n^{2} - n^{2} = 3$

查看试题解析
4. 如图，小李在某运动APP中，设定了每天的步数目标为8000步，该APP用目标线上方或下方的柱状图表示每天超过或少于目标数的步数，如3日，小李少于500目标数的步数500步，则从2日到5日这四天中小李一共走的步数为（）

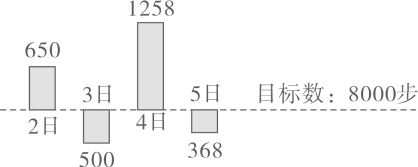A、33040步 B、34776步 C、32000步 D、32000步

查看试题解析
5. 如图为某班50名学生上学路上花费时间的频数分布直方图（每组数据含最大值但不含最小值）．从左起第一、二、三、四个小长方形的高的比为2：4：3：1，则上学路上花费时间超过30min的学生为（）人．

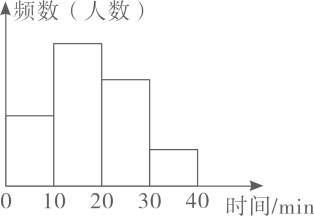A、25 B、20 C、5 D、1

查看试题解析
6. 2023年10月1日是中华人民共和国成立74周年，如图是一个立方体展开图，把展开图折叠成正方体后，“乐”字一面的相对面上的字是（）

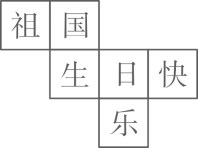A、祖 B、国 C、日 D、快

查看试题解析
7. 如图，数轴上点A、点B分别表示有理数a，b，下列四个式子的结果为正数的是（）

A、 $a + b$ B、 $a - b$ C、 $a b$ D、 $a^{3}$

查看试题解析
8. 如果线段AB＝5cm，线段BC＝4cm，那么A，C两点之间的距离是（）

A、9cm B、1cm C、1cm或9cm D、以上答案都不对

查看试题解析
9. 如果一个角的余角与它的补角互补，则这个角为（）

A、25° B、30° C、40° D、45°

查看试题解析
10. 下列说法：①整数和分数统称为有理数；②数a的相反数是－a；③如果 $a > b$ ，那么 $| a | > | b |$ ；④对我国神舟十六号所有零部件质量情况的调查适合采用全面调查；⑤若小红在小刚的南偏西 $30 °$ 方向，那么小刚在小红的北偏东30°方向；⑥倒数等于本身的数是 $+ 1$ 、－1、0．
其中正确的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题（每题3分，共24分）

11. 小陈同学买了5本笔记本，12支圆珠笔，设笔记本的单价为a元，圆珠笔的单价为b元，则小陈同学共花费元．（用含a，b的代数式表示）

查看试题解析
12. 单项式 $- 3 m^{2} n$ 的次数为．

查看试题解析
13. 比较大小： $- \frac{1}{2}$ $- \frac{1}{3}$ （填“ $>$ ”，“ $<$ ”或“ $=$ ”）．

查看试题解析
14. 单项式 $- 2 x^{m} y^{4}$ 与单项式 $4 x^{2} y^{n}$ 是同类项，则 $m + n$ 的值是．

查看试题解析
15. 现规定一种新的运算“ $*$ ”： $a * b = a^{b}$ ，如 $3 * 2 = 3^{2} = 9$ ，则 $(- \frac{1}{2}) * 2 =$ ．

查看试题解析
16. 延长线段AB到点C，使BC＝2AB，取AC中点D，BD＝1，则AC＝．

查看试题解析
17. 下午2点30分时，分针与时针所成的角的度数为 $°$ ．

查看试题解析
18. OC是从∠AOB的顶点O引出的一条射线，若∠AOB＝70°，∠AOB＝2∠BOC，则∠AOC的度数是 $°$ ．

查看试题解析

三、解答题（第19题，每题3分，共12分，第20题6分，第21－22题每题7分，共14分，第23－25题每题8分，共24分，第26题10分，共66分）

19. 计算：

(1)、 $136 ° 4 5^{'} + 33 ° 2 5^{'}$

(2)、 $(- 16) - (- 7) - | - 4 |$

(3)、 $\frac{7}{6} \times (\frac{1}{6} - \frac{1}{3}) \div \frac{3}{14} \div \frac{7}{3}$

(4)、 $- 4^{2} + [32 \div {(- 2)}^{3} - 16 \times 5]$

查看试题解析
20. 先化简，再求值： $6 a^{2} - 2 (a^{2} - 3 b^{2}) + 4 (a^{2} - b^{2})$ ，其中 $a = - \frac{1}{2}$ ， b＝3．

查看试题解析
21. 如图，已知平面上四个点A，B，C，D，请按要求回答下列问题：

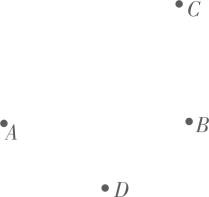
⑴画直线AB，射线BD，连接AC；

⑵取线段AD中点E；

⑶请在直线AB上确定一点F，使点F到点E与点C的距离之和最短，此画图的依据是．（保留作图痕迹）．

查看试题解析
22. 每年的4月24日为中国航天日，为弘扬航天精神，某校开展了航天知识竞答活动，学校随机抽取了六年级的部分同学，并对他们的成绩进行整理（满分为100分，将抽取的成绩在60－70分之间的记为A组，70－80分之间的记为B组，80－90分之间的记为C组，90－100分之间的记为D组，每个组都含最大值不含最小值，例如A组包括70分不包括60分），得到如下不完整的频数分布直方图与扇形统计图：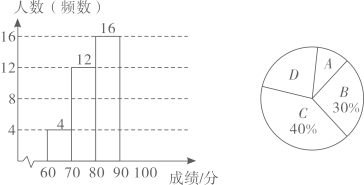

(1)、请求出学校抽取的六年级同学的人数；

(2)、请求出D组的人数并把条形统计图补充完整；

(3)、学校将此次竞答活动的D组成绩记为优秀，已知该校六年级共有800名学生，请估计六年级学生中航天知识掌握情况达到优秀等级的人数．

查看试题解析
23. 某巡警骑摩托车在一条东西大道上巡逻．某天他从岗亭出发，晚上停留在A处．规定向东方向为正，当天行驶记录如下（单位：千米）：
＋10，－8，＋6，－13，＋7，－12，＋3，－1

(1)、A在岗亭何方？通过计算说明A距离岗亭多远？

(2)、在岗亭东面6千米处有个加油站，该巡警巡逻时经过加油站次．

(3)、若摩托车每行1千米耗油0.05升，那么该摩托车这天巡逻共耗油多少升？

查看试题解析
24. 阅读材料：我们知道， $4 x - 2 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) - 2 (a + b) + (a + b) = (4 - 2 + 1) (a + b) = 3 (a + b)$ ． “整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛，尝试应用整体思想解决下列问题：

(1)、把 ${(a - b)}^{2}$ 看成一个整体，合并 $2 {(a - b)}^{2} - 6 {(a - b)}^{2} + 5 {(a - b)}^{2}$ ；

(2)、已知 $x^{2} - 2 y = - 2$ ，求 $6 x^{2} - 12 y - 15$ 的值；

(3)、已知 $a - 2 b = - 1$ ， $2 b - c = 5$ ， $c - d = - 10$ ，求 $(a - c) + (2 b - d) - (2 b - c)$ 的值．

查看试题解析
25. 如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC＝60°，将一直角三角板的直角顶点放在点O处，一边ON在射线OB上，另一边OM在直线AB的上方．

(1)、在图①中，∠COM＝度；

(2)、将图①中的三角板绕点O按逆时针方向旋转，使得ON在∠BOC的内部，如图②，若 $∠ N O C = \frac{1}{6} ∠ M O A$ ，求∠BON的度数；

(3)、将图①中的三角板绕点O以每秒15°的速度沿逆时针方向旋转一周，在旋转的过程中，当直线ON恰好平分锐角∠BOC时，旋转的时间是秒．（直接写出结果）

查看试题解析
26. 已知数轴上两点A，B对应的数分别为－2，4，点P为数轴上一动点，其对应的数为 $x_{P}$ ．

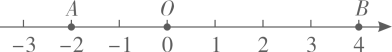(1)、若点P为线段AB的中点，则点P对应的数 $x_{P} =$ ；

(2)、点P在移动的过程中，其到点A、点B的距离之和为8，求此时点P对应的数 $x_{P}$ 的值；

(3)、对于数轴上的三点，给出如下定义：若当其中一个点与其他两个点的距离恰好满足2倍关系时，则称该点是其他两个点的“2倍点”．如图，原点O是点A，B的2倍点．
现在，点A、点B分别以每秒4个单位长度和每秒1个单位长度的速度同时向右运动，同时点P以每秒3个单位长度的速度从表示数5的点向左运动．设出发t秒后，点P恰好是点A，B的“2倍点”，请求出点P第一次是A，B的“2倍点”时t的值，并直接写出满足条件的其它t值．

查看试题解析