黑龙江省哈尔滨市南岗区重点中学2022-2023学年七年级（下）期末数学试卷（五四学制）

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、选择题（本大题共6小题，共18.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列方程组中，是二元一次方程组的是（）

A、 ${\begin{array}{l} x - y + x y = 4 \\ 3 x - y = 4 \end{array}$ B、 ${\begin{array}{l} 4 x + 3 y = 6 \\ 2 y + z = 4 \end{array}$ C、 ${\begin{array}{l} x + y = 4 \\ x - y = 1 \end{array}$ D、 ${\begin{array}{l} x + y = 5 \\ x^{2} + y^{2} = 13 \end{array}$

查看试题解析
2. 已知 $a > b$ ，则下列不等式一定成立的是（）

A、 $a + 2 > b + 3$ B、 $- 2 a > - 2 b$ C、 $\frac{a}{2} < \frac{b}{2}$ D、 $a - 2 > b - 2$

查看试题解析
3. 下列四个图形中，线段 $B E$ 是 $△ A B C$ 的高的图形是（）

A、 B、 C、 D、

查看试题解析
4. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，某校调查了一个班 $50$ 名学生每天的睡眠时间，绘成睡眠时间条形统计图如图所示，则所调查学生睡眠时间的平均数和中位数分别为（）

A、 $7.56 h$ ， $7.5 h$ B、 $7.58 h$ ， $7 h$ C、 $7.58 h$ ， $7.5 h$ D、 $7.56 h$ ， $8 h$

查看试题解析
5. 如图，已知 $D$ 为 $△ A B C$ 边 $B C$ 延长线上一点， $D F ⊥ A B$ 于 $F$ 交 $A C$ 于 $E$ ， $∠ A = 40 °$ ， $∠ D = 50 °$ ，则 $∠ A C D$ 的度数为（）

A、 $60 °$ B、 $70 °$ C、 $80 °$ D、 $90 °$

查看试题解析
6. 如图，△ABC中，AD是它的角平分线，P是AD上的一点，PE∥AB交BC于点E，PF∥AC交BC于点F，G为EF的中点，若PE=3，PF=6，则S_△PED：S_△PDG=（）

A、 $2$ B、 $3$ C、 $\frac{3}{2}$ D、 $\frac{5}{3}$

查看试题解析

二、填空题（本大题共10小题，共30.0分）

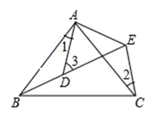
7. $x$ 的 $4$ 倍与 $3$ 的差不大于 $7$ ，用不等式表示为．

查看试题解析
8. 甲、乙两人在相同的条件下，各射靶 10 次，经过计算：甲、乙的平均数均是 7，甲的方差是 1.5，乙的方差是 2.3，的成绩稳定．

查看试题解析
9. 若 $\frac{1}{2} x^{2 m - 1} - 8 > 5$ 是一元一次不等式，则 $m =$ ．

查看试题解析
10. 若一个正 $n$ 边形的每个内角都等于 $120 °$ ，则 $n =$ ．

查看试题解析
11. 如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=20°，∠2=25°，则∠3= ．

查看试题解析
12. 如果不等式 ${\begin{array}{l} x < 8 \\ x > m \end{array}$ 解集为 $m < x < 8$ ，那么 $m$ 的取值范围是．

查看试题解析
13. 如图， $A D$ 是 $∠ C A E$ 的平分线， $∠ B = 35 °$ ， $∠ D A E = 55 °$ ，则 $∠ A C D =$ ．

查看试题解析
14. 每年的4月23日是“世界读书日” $.$ 某中学为了了解八年级学生的读书情况，随机调查了50名学生的读书数量，统计数据如表所示．
数量 $/$ 册
0
1
2
3
4
人数
3
13
16
17
1
在这组统计数据中，若将这50名学生读书册数的众数记为 $m$ ，中位数记为 $n$ ，则 $m n =$ ．

查看试题解析
15. 已知 $A D$ 为 $△ A B C$ 的高线， $A E$ 为角平分线，当 $∠ B = 40 °$ ， $∠ A C D = 60 °$ 时， $∠ E A D =$ 度．

查看试题解析
16. 在等边三角形ABC中，点F是线段AC上一点，点E是线段BC上一点，BF与AE交于点H，∠BAE＝∠FBC，AG⊥BF，∠GAF：∠BEA＝1：10，则∠BAE＝°.

查看试题解析

三、计算题（本大题共1小题，共8.0分）

17. 一个被墨水污染了的方程组： ${\begin{array}{l} * x + * y = 2 \\ * x - 7 y = 8 \end{array}$ ，小明回忆道：“这个方程组的解是 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ ，而我求的解是 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ ，经检验后发现，我的错误是由于看错了第二个方程中的系数所致”根据小明的回忆，你能求出原方程组吗？

查看试题解析

四、解答题（本大题共8小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）

18. 解下列方程组：

(1)、 ${\begin{array}{l} 2 x - y = 5 \\ 7 x - 3 y = 20 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x - 2 y = 9 \\ 2 x + 3 y = - 7 \end{array}$ ．

查看试题解析
19. 解不等式组．

(1)、解不等式 $\frac{x - 2}{2} - (x - 1) < 1$

(2)、解不等式组 ${\begin{array}{l} - 3 (x - 2) \geq 4 - x \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$

查看试题解析
20. 为保护环境，增强居民环保意识，某校积极参加即将到来的 $6$ 月 $5$ 日的“世界环境日”宣传活动，七年级 $(1)$ 班所有同学在同一天调查了各自家庭丢弃塑料袋的情况，统计结果的条形统计图如下：

根据统计图，请回答下列问题：

(1)、这组数据共调查了居民有多少户？

(2)、这组数据的居民丢弃塑料袋个数的中位数是个，众数是个．

(3)、该校所在的居民区约有 $3000$ 户居民，估计该居民区每天丢弃的塑料袋总数大约是多少？

查看试题解析
21. 如图，在 $8 \times 8$ 的网格中，每一小格均为正方形且边长是 $1$ ，已知 $△ A B C$ ．

(1)、画出 $△ A B C$ 中 $A B$ 边上的高 $C E$ ；

(2)、用一条线段将 $△ A B C$ 分成面积相等的两部分 $($ 线段的端点是小正方形的顶点 $)$ ；

(3)、画一个格点三角形，使之与 $△ A B C$ 全等．

查看试题解析
22. 如图， $△ A B C$ 中， $A B = 2 c m$ ， $B C = 4 c m$ ， $C E ⊥ A B$ ， $A D ⊥ B C$ ， $A D$ 和 $C E$ 交于点 $F$ ， $∠ B = 50 °$ ．

(1)、求 $∠ A F C$ 的度数；

(2)、若 $A D = \frac{3}{2} c m$ ，求 $C E$ 的长．

查看试题解析
23. 阅读以下例题：解不等式： $(x + 4) (x - 1) > 0$ ．
解： $①$ 当 $x + 4 > 0$ ，则 $x - 1 > 0$ ，

即可以写成： ${\begin{array}{l} x + 4 > 0 \\ x - 1 > 0 \end{array}$ ，解不等式组得： ${\begin{array}{l} x > - 4 \\ x > 1 \end{array}$ ．

      $∴ x > 1$ ．

      $②$ 当若 $x + 4 < 0$ ，则 $x - 1 < 0$ ，

即可以写成： ${\begin{array}{l} x + 4 < 0 \\ x - 1 < 0 \end{array}$ ，解不等式组得： ${\begin{array}{l} x < - 4 \\ x < 1 \end{array}$ ．

      $∴ x < - 4$ ．

综合以上两种情况：原不等式的解集为： $x > 1$ 或 $x < - 4$ ．

以上解法的依据为：当 $a b > 0$ ，则 $a b$ 同号．

请你模仿例题的解法，解不等式：

(1)、 $(x + 2) (x - 3) > 0$ ；

(2)、 $(3 x - 1) (2 x + 4) < 0$ ．

查看试题解析
24. 某机械厂甲、乙两个生产车间承担生产同一种零件的任务，甲、乙两车间共有50人，甲车间平均每人每天生产零件30个．乙车间平均每人每天生产零件20个，甲车间每天生产零件总数与乙车间每天生产零件总数之和为1300个．

(1)、求甲、乙两车间各有多少人？

(2)、该机械厂改进了生产技术．在甲、乙两车间总人数不变的情况下，从甲车间调出一部分人到乙车间．调整后甲车间平均每人每天生产零件35个，乙车间平均每人每天生产零件25个，若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于1480个，求从甲车间最多调出多少人到乙车间．

查看试题解析
25. 在四边形 $A B C D$ 中， $A D = B C$ ， $A B = C D$ ．

(1)、如图 $1$ ，连接 $A C$ ，求证： $A B / / C D$ ；

(2)、如图 $2$ ，在 $C B$ 的延长线上取一点 $M$ ，连接 $D M$ ，在 $D M$ 上取一点 $L$ ，连接 $B L$ ，当 $∠ C B L = 2 ∠ M$ 时，求证： $L B = M B$ ；

(3)、如图 $3$ ，在 $(2)$ 条件下， $C E$ 平分 $∠ A C B$ 交 $D M$ 于 $E$ 点，连接 $A E$ ，当 $A E ⊥ C E$ ， $B L = 8$ 时，求 $A C$ 的长．

查看试题解析

数量 $/$ 册	0	1	2	3	4
人数	3	13	16	17	1