辽宁省铁岭市铁岭县2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、选择题：（下列各题的备选答案中只有一个是正确的，请将正确的答案序号填入下表相应处，每小题2分，共20分．）

1. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{22}{7}}$ C、 $\sqrt{8}$ D、 $\sqrt{3}$

查看试题解析
2. 下列关于正比例函数 $y = - 2 x$ 的结论正确的是（）

A、直线经过第一、三象限 B、y随x的增大而减小 C、直线经过点（-1，-2） D、不论x取何值时，总有 $y < 0$

查看试题解析
3. 如果一组数据从小到大的顺序排列为：-1，0，4，x ， 6，15，且这组数据的中位数为5，那么这组的数据的众数为（）

A、6 B、5.5 C、5 D、4

查看试题解析
4. 在平行四边形ABCD中， $∠ A = 40 °$ ，则 $∠ C$ 的度数是（）

A、140° B、130° C、40° D、50°

查看试题解析
5. 如图，矩形ABCD中，图中五个小矩形的周长和为14，BC=4，则对角线AC的长为（）

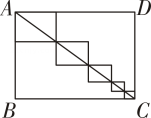A、5 B、7 C、8 D、14

查看试题解析
6. 经过两点（2，3）、（-1，-3）的一次函数的解析式为（）

A、 $y = x + 1$ B、 $y = x - 2$ C、 $y = 2 x - 1$ D、 $y = - 2 x + 1$

查看试题解析
7. 计算： $\sqrt{12} \times \sqrt{\frac{1}{3}} - \sqrt{8} \div \sqrt{2}$ 的结果是（）

A、2 B、0 C、-2 D、 $- \sqrt{2}$

查看试题解析
8. 四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是（）

A、AB=CD B、AD=BC C、AB=BC D、AC=BD

查看试题解析
9. 星期天小明步行从家去图书馆，中间要经过超市小明以a米/分的速度匀速到达超市，再以b米/分的速度匀速到达图书馆，图中的折线OAB反映了小明从家步行到图书馆所走的路程S（米）与行驶时间t（分）的关系，根据图中提供的信息，则 $a ： b$ 的值为（）

A、 $12 ： 7$ B、 $12 ： 5$ C、 $2 ： 1$ D、无法判定

查看试题解析
10. 如图，点O是正方形ABCD的对角线AC的中点，点K在边AD上，连接BK ，分别过点A ， C作BK的垂线，乘足分别为M ， N ．连接OM ， ON ，有以下四个结论：①AM=BN；② $∠ K A M = ∠ B C N$ ；③ $△ O M N$ 是等腰直角三角形；④MN=AM ．其中一定正确的结论有（）

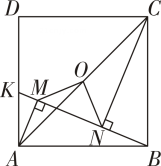A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题：（每小题2分，共16分）

11. 直线 $y = - 2 x + 3$ 不经过第象限．

查看试题解析
12. 计算： $(\sqrt{18} - \sqrt{8}) \div \sqrt{2} =$ ．

查看试题解析
13. 若一个三角形的周长为 $12 \sqrt{3}$ ，一边长为 $3 \sqrt{3}$ ，其它两边之差为 $\sqrt{3}$ ，则这个三角形是三角形．

查看试题解析
14. 数据2019，2020，2021，2022，2023的方差为．

查看试题解析
15. 已知菱形ABCD的两条对角线分别为AC=10，BD=24，则菱形的高为．

查看试题解析
16. 小李从丹东通过快递公司给在铁岭的外婆寄草莓，寄快递时，该公司除每次收取6元的包装费外，不超过1千克，收费20元，每超过1千克时，则超出部分按每千克10元加收费．若小李给外婆快寄了 $x (x > 1)$ 千克草莓，则快寄的费用y（元）与x（千克）之间的函数关系式为．

查看试题解析
17. 如图在同一平面内的两 $▱ A B C D$ 和 $▱ C D E F$ 的周长相等，且 $∠ B A D = 60 °$ ， $∠ F = 110 °$ ，则 $∠ D A E =$ °．

查看试题解析
18. 如图，正方形 $A_{1} B_{1} C_{1} O$ ， $A_{2} B_{2} C_{2} C_{1}$ ， $A_{3} B_{3} C_{3} C_{2} ⋯$ ，按如图所示放置，点 $A_{1}$ ， $A_{2}$ ， $A_{3} ⋯$ 都在直线 $y = x + 1$ 上，点 $C_{1}$ ， $C_{2}$ ， $C_{3} ⋯$ 都在x轴上，则点 $A_{2023}$ 的坐标是．

查看试题解析

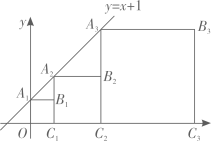
三、解答题（7小题，共64分）

19. 计算：

(1)、 $\sqrt{45} - \sqrt{\frac{2}{5}} \times \sqrt{50}$

(2)、 $(\sqrt{6} + \sqrt{10} \times \sqrt{15}) \div \sqrt{3}$

(3)、 $(3 - \sqrt{7}) (3 + \sqrt{7}) + \sqrt{2} (2 - \sqrt{2})$

(4)、 ${(2 - \sqrt{3})}^{2} + 8 | - \frac{\sqrt{3}}{2} | + {(\sqrt{2})}^{0}$

查看试题解析
20. 王大爷承包了一个鱼塘，投放了2000条某种鱼苗，经过了一段时间的精心喂养，存活率大致达到了90%．他近期想出售鱼塘里的这种鱼，为了估计鱼塘里这种鱼的总质量，王大爷随机捕捞了20条鱼，分别称得其质量后再放回鱼塘现将这20条鱼的质量作为样本，统计结果如下图所示．

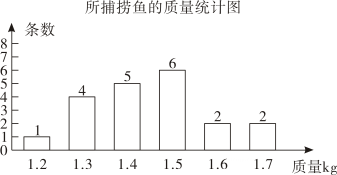(1)、样本中这20条鱼的质量的中位数是kg，众数是kg．

(2)、求这20条鱼的质量的平均数．

(3)、经了解，近期市场上这种鱼的售价为18元/kg，请你利用（2）中的样本平均数，估计王大爷近期销售完鱼塘里的这种鱼收入多少元？

查看试题解析
21. 如图，已知 $A B ： B C ： C D ： D A = 2 ： 2 ： 3 ： 1$ ，且 $∠ A B C = 90 °$ ，求 $∠ D A B$ 的度数．

查看试题解析
22. 如图点O为 $▱ A B C D$ 的对角线AC的中点，过点O作任意一条直线交AD ， BC于点E ， F ，连接AF ， CE ，那么四边形AECF是平行四边形吗？请说明理由．

查看试题解析
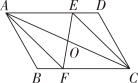23. 如图，在平面直角坐标系中，一次函数 $y_{1} = k x + b$ 的图象经过点入A（-2，6）与x轴交于点B ，与正比例函数 $y_{2} = 3 x$ 的图象交于点C ，且点C的横坐标为1．

(1)、求k ， b的值；

(2)、由图象可知，当x时， $y_{1} > y_{2}$ ；

(3)、若点D在y轴的负半轴上，且满足 $S_{△ C O D} = \frac{1}{3} S_{△ B O C}$ ，求点D的坐标．

查看试题解析
24. 先化简，再求值：
$(\frac{2 x + y}{x^{2} - y^{2}} + \frac{3 y}{y^{2} - x^{2}}) \div (\frac{1}{x^{2} y + x y^{2}})$ ，其中 $x = \sqrt{2}$ ， $y = \sqrt{10}$ ．

查看试题解析
25. 四边形ABCD是正方形，点E为对角线AC上一动点，连接DE ，过点E作 $E F ⊥ D E$ ．交射线BC于点F ．以DE ， EF为边作矩形DEFG ．

(1)、如图1，当 $∠ A E D > 90 °$ 时，点F落在BC边上，则矩形DEFG是；

(2)、当 $∠ A E D < 90 °$ 时，点F落在BC的延长线上，请在图2中按要求画出图形；求证：四边形DEFG是正方形．

(3)、当 $∠ A E D = 90 °$ ，且AB=2时，连接CG ，求CG的长，

查看试题解析