辽宁省锦州市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列四种标志图案中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 若 $x > y$ ，则下列不等式成立的是（）

A、 $x - 3 < y - 3$ B、 $- 2 x > - 2 y$ C、 $\frac{x}{2} > \frac{y}{2}$ D、 $- x + 2 > - y + 2$

查看试题解析
3. 要使分式 $\frac{x}{x - 2023}$ 有意义，则 $x$ 的取值应满足（）

A、 $x = 2023$ B、 $x > 2023$ C、 $x < 2023$ D、 $x \neq 2023$

查看试题解析
4. 下列因式分解正确的是（）

A、 $x^{2} + 9 = (x + 3)^{2}$ B、 $a^{2} + 2 a + 4 = (a + 2)^{2}$ C、 $a^{3} - 4 a^{2} = a^{2} (a - 4)$ D、 $1 - 4 x^{2} = (1 + 4 x) (1 - x)$

查看试题解析
5. 如图，在▱ $A B C D$ 中， $A E ⊥ C D$ 于点 $E$ ， $∠ D A E = 30 °$ ，则 $∠ B$ 等于（）

A、 $30 °$ B、 $40 °$ C、 $45 °$ D、 $60 °$

查看试题解析
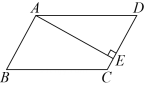6. 如图，桌面上有一把直尺和一个透明的学具 $△ A B C$ ，其中 $∠ A B C = 90 °$ ， $A B = 6 c m$ ， $A C = 10 c m$ ，学具 $△ A B C$ 放置在直尺的一侧， $A B$ 边与直尺的边缘重合，点 $A$ 对应直尺的刻度为 $2 c m .$ 现将学具 $△ A B C$ 沿直尺边缘平移到 $△ A' B C'$ 所在位置，点 $A'$ 对应直尺的刻度为 $17 c m$ ，连接 $C C'$ ，则边 $A C$ 扫过的面积为（）

A、 $120 c m^{2}$ B、 $102 c m^{2}$ C、 $90 c m^{2}$ D、 $72 c m^{2}$

查看试题解析
7. 牛顿曾说过：反证法是数学家最精良的武器之一，我们用反证法证明命题“三角形中不能两个直角”，应先假设（）

A、三角形中有一个内角是直角 B、三角形中有两个内角是直角 C、三角形中有三个内角是直角 D、三角形中不能有内角是直角

查看试题解析
8. 小明在化简分式 $\frac{3 n}{m - 2 n} + \frac{2 m - n}{2 n - m}$ 的过程中，因为其中一个步骤的错误，导致化简结果是错误的，小明开始出现错误的那一步是（）
原式 $= \frac{3 n - (2 m - n)}{m - 2 n} \dots ①$
      $= \frac{4 n - 2 m}{m - 2 n} \dots ②$
      $= \frac{2 (2 n - m)}{m - 2 n} \dots ③$
      $= 2 \dots ④$

A、 $①$ B、 $②$ C、 $③$ D、 $④$

查看试题解析
9. 如图，下列四种用无刻度直尺和圆规作角平分线的方法，其中不正确的个数是（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
10. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D$ ， $∠ A B C = 2 ∠ D A C$ ，若 $A B = 6$ ， $A C = 4$ ，则 $C D$ 的长为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{2 \sqrt{5}}{3}$ D、 $2$

查看试题解析

二、填空题（本大题共6小题，共12.0分）

11. 多项式 $3 x^{2} y^{3} z - 9 x^{3} y^{3} z$ 各项的公因式是．

查看试题解析
12. 如图，这是在数轴上分别表示的一个不等式组中两个不等式的解集，则这个不等式组的解集是．

查看试题解析
13. 如图，直线 $y = 2 x - 1$ 与直线 $y = k x + b (k < 0)$ 相交于点 $P (2 ， 3)$ ，根据图象可知，关于 $x$ 的等式 $2 x - 1 > k x + b$ 的解集是．

查看试题解析
14. 一个正多边形的一个内角比它的外角的2倍多60°，则它的边数是．

查看试题解析
15. 关于 $x$ 的方程 $\frac{3 x - 2}{x + 1} = \frac{m}{x + 1} + 1$ 无解，则 $m$ 的值为．

查看试题解析
16. 如图，在▱ $A B C D$ 中，对角线 $A C$ ， $B D$ 交于点 $O$ ， $∠ A C D = 30 °$ ， $A C = 4$ ，过点 $C$ 作 $∠ C A B$ 的平分线的垂线，垂足为点 $E$ ，若点 $O$ 在 $A E$ 的垂直平分线上， $P$ 是直线 $A B$ 上的动点，则 $O P + P E$ 的最小值为．

查看试题解析

三、解答题（本大题共9小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）

17. 解不等式组： ${\begin{array}{l} \frac{1}{2} (x + 4) \leq 2 \\ x - 3 (x - 1) > 5 \end{array}$ ．

查看试题解析
18. 解分式方程： $\frac{1}{x - 3} + 3 = \frac{x}{3 - x}$ .

查看试题解析
19. 先化简，再求值： $(\frac{3 x + 4}{x^{2} - 1} - \frac{2}{x - 1}) \div \frac{x + 2}{x^{2} - 2 x + 1}$ ，其中 $x = 3$ ．

查看试题解析
20. 如图，在平面直角坐标系中，已知 $A (1 ， 4)$ ， $B (3 ， 1)$ ， $C (5 ， 2)$ ．

(1)、画出将 $△ A B C$ 沿着 $x$ 轴的反方向平移 $6$ 个单位得到的 $△ A_{1} B_{1} C_{1}$ ；

(2)、画出将 $△ A B C$ 绕原点 $O$ 旋转 $180 °$ 后得到的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $B_{2}$ 的坐标；

(3)、画出的 $△ A_{1} B_{1} C_{1}$ 和 $△ A_{2} B_{2} C_{2}$ 是中心对称图形吗？如果是，请写出对称中心的坐标，如果不是，请说明理由．

查看试题解析
21. 数形结合是解决数学问题的重要思想方法，借助图形可以对很多数学问题进行直观推导和解释 $.$ 如图 $1$ ，有足够多的 $A$ ， $B$ ， $C$ 三种纸片： $A$ 种是边长为 $m$ 的正方形， $B$ 种是边长为 $n$ 的正方形， $C$ 种是宽为 $m$ ，长为 $n$ 的长方形 $.$ 用 $A$ 种纸片 $1$ 张， $B$ 种纸片 $1$ 张， $C$ 种纸片 $2$ 张可以拼出 $($ 不重不漏 $)$ 如图 $2$ 所示的正方形 $.$ 根据正方形的面积，可以用来解释整式乘法 $(m + n) (m + n) = m^{2} + 2 m n + n^{2}$ ，反过来也可以解释多项式 $m^{2} + 2 m n + n^{2}$ ，因式分解的结果为 $m^{2} + 2 m n + n^{2} = (m + n)^{2}$ ，依据上述积累的数与形对应关系的经验，解答下列问题：

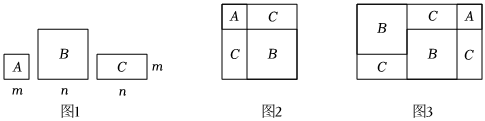(1)、若多项式 $m^{2} + 2 n^{2} + 3 m n$ 表示分别由 $1$ ， $2$ ， $3$ 张 $A$ ， $B$ ， $C$ 三种纸片拼出如图 $3$ 所示的大长方形的面积，请根据图形求出这个长方形的长和宽，并对多项式 $m^{2} + 3 m n + 2 n^{2}$ 进行因式分解；

(2)、我们可以借助图 $3$ 再拼出一个更大的长方形，使该长方形刚好由 $3$ 张 $A$ 种纸片， $2$ 张 $B$ 种纸片， $7$ 张 $C$ 种纸片拼成，那么这个长方形的面积可以表示为多项式，据此可得到该多项式因式分解的结果为．

查看试题解析
22. 为了改善锦州的交通状况，政府投资修建北外环公路 $.$ 某筑路工程公司中标了一段 $3000 m$ 公路的路基工程，计划在规定时间完成 $.$ 为了向“七，一”献礼，公司决定加快工程进度实际平均每天完成的工程量是原计划的 $1.2$ 倍，结果提前 $10$ 天完成任务，那么该筑路工程公司实际每天完成路基多少米？ $($ 要求用方程求解 $)$

查看试题解析
23. 为了美化校园环境，某校计划在花卉批发市场购买月季和芍药两种花苗栽种在校园内 $.$ 已知每株月季花苗比每株芍药花苗少 $2$ 元，用 $125$ 元购买月季花苗的株数与用 $175$ 元购买芍药花苗的株数相同．

(1)、求每株月季花苗和每株芍药花苗分别多少元；

(2)、该校决定购买月季和芍药两种花苗共 $400$ 株，总费用不超过 $2350$ 元，那么最少能购买多少株月季花苗？ $($ 要求(1)(2)用方程或不等式求解 $)$

查看试题解析
24.
【问题情境】：一副三角尺 $A B C$ 和 $D E F$ 中， $∠ A C B = ∠ E D F = 90 °$ ， $∠ A = 45 °$ ， $∠ E = 30 °$ ，在数学课上，同学们用这样的一副三角尺进行摆放，将三角尺 $D E F$ 的直角顶点 $D$ 放在三角尺 $A B C$ 内部，直角边 $D E$ 与 $C A$ 交于点 $G$ ，直角边 $D F$ 与 $C B$ 交于点 $H$ ．
【实验探究】：

(1)、如图 $1$ ，勤学小组的同学发现任意改变三角尺 $D E F$ 的位置， $∠ C G D + ∠ C H D$ 的度数都为 $180 °$ ，请说明理由；

(2)、如图 $2$ ，善思小组的同学改变三角尺 $D E F$ 的位置，将直角顶点 $D$ 放在 $∠ A C B$ 的平分线上，测量发现 $D G = D H$ ，请证明此结论．

查看试题解析
25. 已知 $△ A B C$ 和 $△ A D E$ 都是等边三角形，连接 $B D$ ，将 $B D$ 绕点 $B$ 逆时针旋转 $60 °$ 得到 $B F$ ，连接 $C E$ ， $E F$ ．

(1)、如图 $1$ ，求证： $① △ A D B$ ≌ $△ A E C$ ；
$②$ 四边形 $B C E F$ 是平行四边形；

(2)、如图 $2$ ， $M$ ， $N$ 分别是 $B C$ ， $B E$ 的中点，若 $△ A D E$ 的顶点 $E$ 在 $A B$ 边上， $A B = 6$ ， $A D = 2$ ，求 $M N$ 的长．

查看试题解析