辽宁省锦州市2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共20.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 汉字是迄今为止持续使用时间最长的文字,是传承中华文化的重要载体.汉字在发展过程中演变出多种字体,给人以美的享受.下面是“北京之美”四个字的篆书,不能看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 中科院发现“绿色”光刻胶,精度可达米.数字用科学记数法可表示为( )A、 B、 C、 D、4. 如果一个三角形的两边长分别为和 , 则第三边长可能是( )A、 B、 C、 D、5. 如图是水平放置的圆形瓷砖,瓷砖上的图案是三条直径把两个同心圆中的大圆分成六等份若在这个大圆区域内随机地抛一个小球,则小球落在阴影部分的概率是( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 中科院发现“绿色”光刻胶,精度可达米.数字用科学记数法可表示为( )A、 B、 C、 D、4. 如果一个三角形的两边长分别为和 , 则第三边长可能是( )A、 B、 C、 D、5. 如图是水平放置的圆形瓷砖,瓷砖上的图案是三条直径把两个同心圆中的大圆分成六等份若在这个大圆区域内随机地抛一个小球,则小球落在阴影部分的概率是( ) A、 B、 C、 D、6. 如图所示的网格由边长相同的小正方形组成,点 , , , , , , 均在小正方形的顶点上,则的重心是( )
A、 B、 C、 D、6. 如图所示的网格由边长相同的小正方形组成,点 , , , , , , 均在小正方形的顶点上,则的重心是( )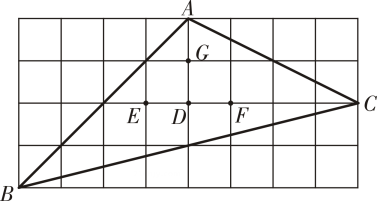 A、点 B、点 C、点 D、点7. 如图,已知 , 添加下列条件,不能使≌的是( )
A、点 B、点 C、点 D、点7. 如图,已知 , 添加下列条件,不能使≌的是( ) A、 B、 C、 D、8. 某科研小组通过实验获取的声音在空气中传播的速度与空气温度之间的一组数据如表:
A、 B、 C、 D、8. 某科研小组通过实验获取的声音在空气中传播的速度与空气温度之间的一组数据如表:空气温度
声速
根据表格中的数据,判定下列说法不正确的是( )
A、在这个变化中,自变量是空气温度,因变量是声速 B、空气温度越高,声速越快 C、当空气温度为时,声音可以传播 D、当空气温度每升高 , 声速相应增加9. 已知:如图,在中,的垂直平分线交于点 , 的垂直平分线交于点若 , 则的度数为( ) A、 B、 C、 D、10. 已知的面积为 , 是边上的高,若 , , 则的长为( )A、 B、或 C、 D、或
A、 B、 C、 D、10. 已知的面积为 , 是边上的高,若 , , 则的长为( )A、 B、或 C、 D、或二、填空题(本大题共8小题,共16.0分)
-
11. 若 , 则 .12. 一辆轿车油箱中存油升,轿车行驶时平均每小时耗油升,则这辆轿车的油箱中剩余油量升与行驶时间小时之间的关系式是 .13. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在的两边、上分别在取 , 移动角尺,使角尺两边相同的刻度分别与点、重合,这时过角尺顶点的射线就是的平分线.利用所学知识可知他构造全等三角形的依据是 .
 14. 苗圃技术人员对某种花苗移植的成活情况进行调查,将调查数据整理后结果如表所示:
14. 苗圃技术人员对某种花苗移植的成活情况进行调查,将调查数据整理后结果如表所示:移植总数
成活数
成活的频率
根据表中数据,估计这种花苗移植的成活概率为精确到
15. 规定两数 , 之间的一种新运算 , 如果 , 那么 , 例如:因为 , 所以;因为 , 所以 , 按以上规定,则 .16. 如图,将长方形纸条折叠,折痕为 , 折叠后点 , 分别落在点 , 处,与交于点 , 若 , 则的度数是 . 17. 把个长和宽分别为 , 的小长方形纸片如图 , 按如图所示的方式放置在长方形中,则长方形中阴影部分的面积为用含有 , 的代数式表示
17. 把个长和宽分别为 , 的小长方形纸片如图 , 按如图所示的方式放置在长方形中,则长方形中阴影部分的面积为用含有 , 的代数式表示 18. 如图等腰三角形的底边长为 , 面积是 , 腰的垂直平分线分别交 , 于点 , , 若点为底边的中点,点为线段上一动点,则的周长的最小值为 .
18. 如图等腰三角形的底边长为 , 面积是 , 腰的垂直平分线分别交 , 于点 , , 若点为底边的中点,点为线段上一动点,则的周长的最小值为 .
三、解答题(本大题共7小题,共64.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算:(1)、;(2)、 .20. 先化简,再求值: , 其中 , .21. 如图,在中, , 于点 .
 (1)、尺规作图:作的角平分线,交于点 , 交于点;(保留作图痕迹,不写作法)(2)、若 , 求的度数.22. 看图填空:请将不完整的解题过程及根据补充完整
(1)、尺规作图:作的角平分线,交于点 , 交于点;(保留作图痕迹,不写作法)(2)、若 , 求的度数.22. 看图填空:请将不完整的解题过程及根据补充完整
如图, , 试说明: .
理由:
因为已知 ,
根据“ ▲ ”,
所以 ▲ ,
又因为已知 ,
所以 ,
根据“ ▲ ”,
所以 ,
根据“ ▲ ”,
所以 .
23. 某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”三种类别的美德少年,每位同学只能参评其中一类,评选后,把最终入选的校园“美德少年”分类统计,制作了如下统计表:类别
人数
频率
助人为乐美德少年
自强自立美德少年
孝老爱亲美德少年
请根据以上信息,解答下列问题:
(1)、统计表中的 , ;(2)、校园小记者决定从入选的“美德少年”中随机采访一位,求被采访到的是自强自立美德少年的概率.24. 赛龙舟是传统节日端午节的主要习俗某市在端午节期间,举行赛龙舟比赛,已知甲、乙两队参加比赛时的路程米与时间分钟之间的关系如图所示,请根据图象,回答下列问题:
 (1)、这次龙舟比赛全程为米;(2)、龙舟比赛先到达终点的是队;填“甲”或“乙”(3)、比赛时甲队龙舟的平均速度是米分钟;(4)、甲队和乙队相遇时,乙队龙舟的速度是米分钟;(5)、直接写出相遇之前甲队和乙队龙舟何时相距米.25.
(1)、这次龙舟比赛全程为米;(2)、龙舟比赛先到达终点的是队;填“甲”或“乙”(3)、比赛时甲队龙舟的平均速度是米分钟;(4)、甲队和乙队相遇时,乙队龙舟的速度是米分钟;(5)、直接写出相遇之前甲队和乙队龙舟何时相距米.25. (1)、【模型构建】
(1)、【模型构建】如图 , 在等腰中, , 点在线段的延长线上,连接 , 则在和中,边的对角和之间的数量关系为;
(2)、【模型应用】如图 , 在和中,为锐角, , , , 试说明:;
(3)、【模型拓展】如图 , , , , , 和交于点 , 试探究与之间的数量关系,并说明理由.