辽宁省营口市大石桥市2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列各根式中,最简二次根式是( )A、 B、 C、 D、2. 下列各组数中,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,103. 下列各式计算错误的是( )A、 B、 C、 D、4. 如图,平行四边形的对角线与相交于点 , , 若 , , 则的长是( )
 A、 B、 C、 D、5. 下列说法中不正确的是( )A、对角线垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、菱形的面积等于对角线乘积的一半 D、对角线互相垂直平分的四边形是正方形6. 某同学对数据26,36,36,46,5■,52进行统计分析.发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数7. 如图,在平面直角坐标系中,的顶点、的坐标分别为、 , , , 过作轴垂线交轴于点 , 作轴垂线交轴于点 , 则矩形的面积为( )
A、 B、 C、 D、5. 下列说法中不正确的是( )A、对角线垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、菱形的面积等于对角线乘积的一半 D、对角线互相垂直平分的四边形是正方形6. 某同学对数据26,36,36,46,5■,52进行统计分析.发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数7. 如图,在平面直角坐标系中,的顶点、的坐标分别为、 , , , 过作轴垂线交轴于点 , 作轴垂线交轴于点 , 则矩形的面积为( ) A、 B、 C、 D、8. 如图,已知函数和的图象交于点 , 则不等式的解集为( )
A、 B、 C、 D、8. 如图,已知函数和的图象交于点 , 则不等式的解集为( ) A、 B、 C、 D、9. 如图,边长为的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM=( )
A、 B、 C、 D、9. 如图,边长为的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM=( ) A、 B、 C、 D、10. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A、 B、 C、 D、10. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )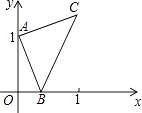 A、
A、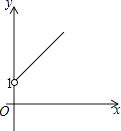 B、
B、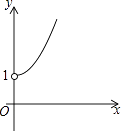 C、
C、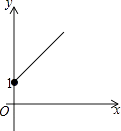 D、
D、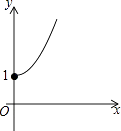
二、填空题(本大题共6小题,共18.0分)
-
11. 函数中,自变量的取值范围是 .12. 若函数是一次函数,则 .13. 若数据1,4, ,9,6,5的平均数为5.则中位数是;众数是.
14. 若直角三角形的两边长为6和8,则第三边长为 .15. 如图,一次函数的图象与轴、轴分别交于点、 , 点在轴上,要使是以为腰的等腰三角形,那么点的坐标是 . 16. 如图,将矩形 折叠,使点 和点 重合,折痕为 , 与 交于点 .若 , ,则 的长为.
16. 如图,将矩形 折叠,使点 和点 重合,折痕为 , 与 交于点 .若 , ,则 的长为.
三、计算题(本大题共1小题,共6.0分)
-
17. 计算: .
四、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 计算: .19. 在杭州西湖风景游船处,如图,在离水面高度为的岸上,有人用绳子拉船靠岸,开始时绳子的长为 , 此人以的速度收绳后船移动到点的位置,问船向岸边移动了多少?假设绳子是直的,结果保留根号
 20. 如图,在▱中,点是边的中点,连接并延长交的延长线于点 , 连接 , .
20. 如图,在▱中,点是边的中点,连接并延长交的延长线于点 , 连接 , . (1)、求证:平分;(2)、若 , , 求▱的面积.21. 甲、乙两车分别从、两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到地,乙车立即以原速原路返回到地甲、乙两车距地的路程与各自行驶的时间之间的关系如图所示.
(1)、求证:平分;(2)、若 , , 求▱的面积.21. 甲、乙两车分别从、两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到地,乙车立即以原速原路返回到地甲、乙两车距地的路程与各自行驶的时间之间的关系如图所示. (1)、 , .(2)、分别求出甲、乙两车距地的距离与行驶的时间之间的函数关系式.(3)、当甲车到达地时,求乙车距地的路程.22. 本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”下面简称:“读书量”进行了随机抽样调查,并对所有随机抽取学生的“读书量”单位:本进行了统计,如图所示:
(1)、 , .(2)、分别求出甲、乙两车距地的距离与行驶的时间之间的函数关系式.(3)、当甲车到达地时,求乙车距地的路程.22. 本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动.校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”下面简称:“读书量”进行了随机抽样调查,并对所有随机抽取学生的“读书量”单位:本进行了统计,如图所示:
根据以上信息,解答下列问题:
(1)、补全上面两幅统计图,填出本次所抽取学生四月份“读书量”的众数为 .(2)、求本次所抽取学生四月份“读书量”的平均数;(3)、已知该校七年级有名学生,请你估计该校七年级学生中,四月份“读书量”为本的学生人数.23. 如图,在▱中,对角线 , 相交于点 , 以为斜边的等腰直角三角形的边 , 与交于点 , 连接 , 使得在上截取 , 连接 , . (1)、判断四边形的形状,并说明理由;(2)、若 , , 求的长.24. 某市风景区门票价格如图所示,现有甲乙两个旅行团队,计划在“十一”黄金周期间到该景点游玩.两团队游客人数之和为人,甲团队人数不超过人,乙团队人数为人,但不足人.如果甲、乙两团队分别购买门票,两团队门票款之和为元.
(1)、判断四边形的形状,并说明理由;(2)、若 , , 求的长.24. 某市风景区门票价格如图所示,现有甲乙两个旅行团队,计划在“十一”黄金周期间到该景点游玩.两团队游客人数之和为人,甲团队人数不超过人,乙团队人数为人,但不足人.如果甲、乙两团队分别购买门票,两团队门票款之和为元. (1)、求关于的关系式,并说明两队联合购票比分别购票最多可节约多少元?(2)、“十一”黄金周之后,该风景区对门票价格作了如下调整:人数不超过人时,门票价格不变;人数超过人但不超过人时,每张门票降价元;人数超过人时,每张门票降价元,若甲、乙两个旅行团队“十一”黄金周之后去游玩,最多节约元,求的值.
(1)、求关于的关系式,并说明两队联合购票比分别购票最多可节约多少元?(2)、“十一”黄金周之后,该风景区对门票价格作了如下调整:人数不超过人时,门票价格不变;人数超过人但不超过人时,每张门票降价元;人数超过人时,每张门票降价元,若甲、乙两个旅行团队“十一”黄金周之后去游玩,最多节约元,求的值.
-