辽宁省盘锦市盘山县2022-2023学年八年级上册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共20.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各式中,不能用平方差公式计算的是( )A、 B、 C、 D、4. 如果分式的值为 , 那么的值为( )A、 B、 C、 D、5. 如图,点是内一点, , , , 则( )
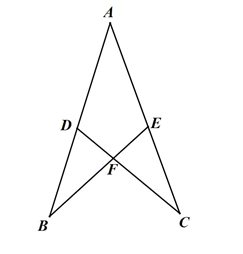
3. 下列各式中,不能用平方差公式计算的是( )A、 B、 C、 D、4. 如果分式的值为 , 那么的值为( )A、 B、 C、 D、5. 如图,点是内一点, , , , 则( ) A、 B、 C、 D、6. 如图,已知 , 要说明 , 需从下列条件中选一个,错误的是( )
A、 B、 C、 D、6. 如图,已知 , 要说明 , 需从下列条件中选一个,错误的是( ) A、 B、 C、 D、7. 若 , 则括号内的整式是( )A、 B、 C、 D、8. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )
A、 B、 C、 D、7. 若 , 则括号内的整式是( )A、 B、 C、 D、8. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )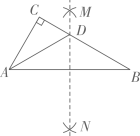 A、20° B、30° C、45° D、60°9. 如图,平分 , 且 , 点为上任意点,于 , , 交于 , 若 , 则的长为( )
A、20° B、30° C、45° D、60°9. 如图,平分 , 且 , 点为上任意点,于 , , 交于 , 若 , 则的长为( ) A、 B、 C、 D、10. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A、 B、 C、 D、10. 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )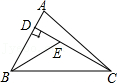 A、10 B、7 C、5 D、4
A、10 B、7 C、5 D、4二、填空题(本大题共9小题,共19.0分)
-
11. 十二边形的内角和是12. 若分式 有意义,则x的取值范围为 .13. 一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是.14. 如图,在中,为直角, , 于若 , 则 .
 15. 约分:① , ② .16. 已知a+b=5,ab=3,则a2+b2= .17. 如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 , P2 , 连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为.
15. 约分:① , ② .16. 已知a+b=5,ab=3,则a2+b2= .17. 如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 , P2 , 连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为.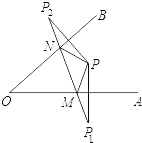 18. 如图,为线段上一动点不与点、重合 , 在同侧分别作正和正 , 与交于点 , 与交于点 , 与交于点 , 连接以下五个结论:;;;; .
18. 如图,为线段上一动点不与点、重合 , 在同侧分别作正和正 , 与交于点 , 与交于点 , 与交于点 , 连接以下五个结论:;;;; .恒成立的结论有把你认为正确的序号都填上
 19. 如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
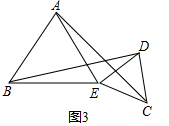
19. 如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.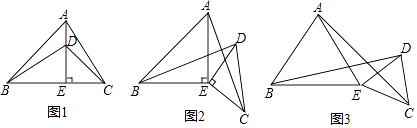 (1)、试判断BD与AC的位置关系和数量关系,并说明理由;(2)、如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;(3)、如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
(1)、试判断BD与AC的位置关系和数量关系,并说明理由;(2)、如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;(3)、如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
三、计算题(本大题共2小题,共12.0分)
-
20. 解方程: .21. 化简:
四、解答题(本大题共5小题,共40.0分。解答应写出文字说明,证明过程或演算步骤)
-
22. 计算:(1)、;(2)、先化简,再求值: , 其中 .23. 因式分解:(1)、;(2)、 .24. 如图,点 D 在 AB 上,点 E 在 AC 上, AB = AC , AD = AE . 求证: ∠B = ∠C .