辽宁省铁岭五中2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列根式中是最简二次根式的是( )A、 B、 C、 D、2. 化简:结果为( )A、 B、 C、 D、3. 下列命题的逆命题正确的是( )A、对顶角相等 B、如果两个实数相等,那么它们的平方相等 C、两直线平行,同旁内角互补 D、全等三角形的对应角相等4. 如图是一张探宝图,根据图中的尺寸,起点到终点的距离是( )
 A、 B、 C、 D、5. 如图,在中, , , 是斜边上的一个动点, , , 垂足分别为 , , 则的最小值为( )
A、 B、 C、 D、5. 如图,在中, , , 是斜边上的一个动点, , , 垂足分别为 , , 则的最小值为( ) A、 B、 C、 D、6. 若一次函数 , 当时, , 则的值为( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,直线与轴,轴交于 , 两点,以为底边在轴的右侧作等腰 , 将沿轴折叠,使点恰好落在直线上,则点的坐标为( )
A、 B、 C、 D、6. 若一次函数 , 当时, , 则的值为( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,直线与轴,轴交于 , 两点,以为底边在轴的右侧作等腰 , 将沿轴折叠,使点恰好落在直线上,则点的坐标为( ) A、 B、 C、 D、8. 如图,直线与直线相交于点 , 则不等式的解集为( )
A、 B、 C、 D、8. 如图,直线与直线相交于点 , 则不等式的解集为( ) A、 B、 C、 D、9. 小洪根据演讲比赛中九位评委所给的分数制作了如下表格:
A、 B、 C、 D、9. 小洪根据演讲比赛中九位评委所给的分数制作了如下表格:平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A、平均数 B、中位数 C、众数 D、方差10. 甲、乙两人赛跑,两人所跑的路程米与所用的时间分的函数关系如图所示,给出下列说法:
①比赛全程米.
②分时,甲,乙相距米.
③比赛结果是乙比甲领先秒到达终点.
④分秒时,乙追上甲,其中正确的个数有个.( )
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
11. 已知 , 则 .12. 如图,在中, , , , , 则 .
 13. 如图正方形ABCD边长为2,E为CD边中点,P为射线BE上一点(P不与B重合),若△PDC为直角三角形,则BP=.
13. 如图正方形ABCD边长为2,E为CD边中点,P为射线BE上一点(P不与B重合),若△PDC为直角三角形,则BP=. 14. 如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为.
14. 如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为. 15. 对于一次函数 y=kx+b , 当 1≤x≤4 时,3≤y≤6,则一次函数的解析式为 .16. 已知一组数据x1 , x2 , …,xn的方差是s2 , 则新的一组数据ax1+1,ax2+1,…,axn+1(a为非零常数)的方差是(用含a和s2的代数式表示).17. 如图,正方形的对角线在直线上,点在第一象限.若正方形的面积是 , 则点的坐标为 .
15. 对于一次函数 y=kx+b , 当 1≤x≤4 时,3≤y≤6,则一次函数的解析式为 .16. 已知一组数据x1 , x2 , …,xn的方差是s2 , 则新的一组数据ax1+1,ax2+1,…,axn+1(a为非零常数)的方差是(用含a和s2的代数式表示).17. 如图,正方形的对角线在直线上,点在第一象限.若正方形的面积是 , 则点的坐标为 . 18. 正方形 , , , 按如图所示的方式放置,点 , , , 和点 , , , 分别在直线和轴上,已知点 , , 则点的坐标是 .
18. 正方形 , , , 按如图所示的方式放置,点 , , , 和点 , , , 分别在直线和轴上,已知点 , , 则点的坐标是 .
三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算:(1)、;(2)、已知 , 求代数式的值.20. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润;(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?
21. 为了解学生参加户外活动的情况,某中学对学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题: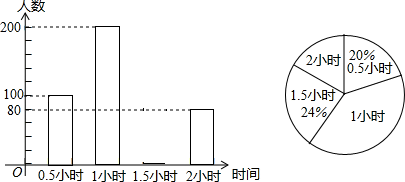 (1)、求户外活动时间为1.5小时的学生有多少人?并补全条形统计图(2)、每天户外活动时间的中位数是小时?(3)、该校共有1800名学生,请估计该校每天户外活动超过1小时的学生人数有多少人?22. 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)、求户外活动时间为1.5小时的学生有多少人?并补全条形统计图(2)、每天户外活动时间的中位数是小时?(3)、该校共有1800名学生,请估计该校每天户外活动超过1小时的学生人数有多少人?22. 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN. (1)、求证:四边形BMDN是菱形;(2)、若AB=4,AD=8,求菱形BMDN的周长和对角线MN的长.23. 如图,在平行四边形中,对角线与相交于点 , 点 , 分别为 , 的中点,延长至 , 使 , 连接 .
(1)、求证:四边形BMDN是菱形;(2)、若AB=4,AD=8,求菱形BMDN的周长和对角线MN的长.23. 如图,在平行四边形中,对角线与相交于点 , 点 , 分别为 , 的中点,延长至 , 使 , 连接 . (1)、求证:≌;(2)、当线段与线段满足什么数量关系时,四边形是矩形?请说明理由.24. 如图 , 点是正方形边上任意一点,以为边作正方形 , 连接 , 点是线段中点,射线与交于点 , 连接 .
(1)、求证:≌;(2)、当线段与线段满足什么数量关系时,四边形是矩形?请说明理由.24. 如图 , 点是正方形边上任意一点,以为边作正方形 , 连接 , 点是线段中点,射线与交于点 , 连接 . (1)、请直接写出和的数量关系和位置关系.(2)、把图中的正方形绕点顺时针旋转 , 此时点恰好落在线段上,如图 , 其他条件不变,(1)中的结论是否成立,请说明理由.(3)、把图中的正方形绕点顺时针旋转 , 此时点、恰好分别落在线段、上,连接 , 如图 , 其他条件不变,若 , , 直接写出的长度.25. 如图 , 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 已知点 .
(1)、请直接写出和的数量关系和位置关系.(2)、把图中的正方形绕点顺时针旋转 , 此时点恰好落在线段上,如图 , 其他条件不变,(1)中的结论是否成立,请说明理由.(3)、把图中的正方形绕点顺时针旋转 , 此时点、恰好分别落在线段、上,连接 , 如图 , 其他条件不变,若 , , 直接写出的长度.25. 如图 , 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 已知点 .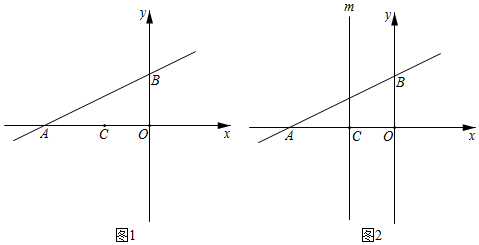 (1)、求出点 , 点的坐标.(2)、是直线上一动点,且和的面积相等,求点坐标.(3)、如图 , 过点作平行于轴的直线 , 在直线上是否存在点 , 使得是等腰直角三角形?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由.
(1)、求出点 , 点的坐标.(2)、是直线上一动点,且和的面积相等,求点坐标.(3)、如图 , 过点作平行于轴的直线 , 在直线上是否存在点 , 使得是等腰直角三角形?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由.