天津市红桥区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-01 类型:期末考试
一、单选题
-
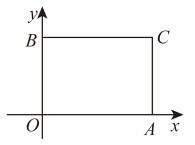
1. 若 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列计算中正确的是( )A、 B、 C、 D、3. 有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的( )A、方差 B、中位数 C、众数 D、平均数4. 已知一个直角三角形的两条直角边的长分别为2和4,则它的斜边的长为( )A、4 B、 C、 D、205. 如图,四边形是矩形,A , B两点的坐标分别是 , , 点C在第一象限,则点C的坐标为( )
 A、 B、 C、 D、6. 将一次函数的图象沿轴向上平移4个单位长度,所得直线的解析式为( )A、 B、 C、 D、7. 在“争创美丽校园”示范校评比活动中,10位评委给某校的评分情况如下表所示:
A、 B、 C、 D、6. 将一次函数的图象沿轴向上平移4个单位长度,所得直线的解析式为( )A、 B、 C、 D、7. 在“争创美丽校园”示范校评比活动中,10位评委给某校的评分情况如下表所示:评分(分)
评委人数
则这10位评委评分的平均数是( )
A、85 B、87.5 C、89 D、908. 如图□ 的对角线交于点 , , ,则 的度数为( )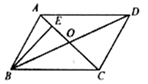 A、50° B、40° C、30° D、20°9. 已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
A、50° B、40° C、30° D、20°9. 已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )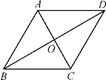 A、16 B、16 C、8 D、810. 已知点 , , 在一次函数(为常数)的图象上,则的大小关系是( )A、 B、 C、 D、11. 如图,正方形的边长为8,点E在上且 , F为对角线上一动点,则周长的最小值为( )
A、16 B、16 C、8 D、810. 已知点 , , 在一次函数(为常数)的图象上,则的大小关系是( )A、 B、 C、 D、11. 如图,正方形的边长为8,点E在上且 , F为对角线上一动点,则周长的最小值为( )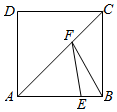 A、6 B、8 C、10 D、1212. 关于函数(为常数),有下列结论:①当时,此函数是一次函数;②无论取什么值,函数图象必经过点;③若图像经过二、三、四象限,则的取值范围是;④若函数图象与轴的交点始终在正半轴,则的取值范围是 . 其中,正确结论的个数是( ).A、1 B、2 C、3 D、4
A、6 B、8 C、10 D、1212. 关于函数(为常数),有下列结论:①当时,此函数是一次函数;②无论取什么值,函数图象必经过点;③若图像经过二、三、四象限,则的取值范围是;④若函数图象与轴的交点始终在正半轴,则的取值范围是 . 其中,正确结论的个数是( ).A、1 B、2 C、3 D、4二、填空题
-
13. 在中, , , 则的周长为 .14. 如图,在四边形中, , , 若 , 则的大小为(度).
 15. 计算(3+)(3-)的结果等于 .16. 将直线向右平移1个单位长度,平移后直线的解析式是 .17. 若一个三角形的三边长分别为 , 3,2,则此三角形的面积为 .18. 如图,一次函数y=x+2的图像与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为 .
15. 计算(3+)(3-)的结果等于 .16. 将直线向右平移1个单位长度,平移后直线的解析式是 .17. 若一个三角形的三边长分别为 , 3,2,则此三角形的面积为 .18. 如图,一次函数y=x+2的图像与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB上的点,且∠OPC=45°,PC=PO,则点P的坐标为 .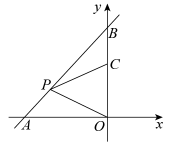
三、解答题
-
19. 计算:(1)、;(2)、 .20. 如图,中,点D是上的一点, , , , .
 (1)、判断与的位置关系,并说明理由;(2)、求的面积.21. 某校为了解学生家中拥有移动设备的情况,随机调查了部分学生家中拥有移动设备的数量.根据统计的结果,绘制出如下的统计图①和图②.
(1)、判断与的位置关系,并说明理由;(2)、求的面积.21. 某校为了解学生家中拥有移动设备的情况,随机调查了部分学生家中拥有移动设备的数量.根据统计的结果,绘制出如下的统计图①和图②.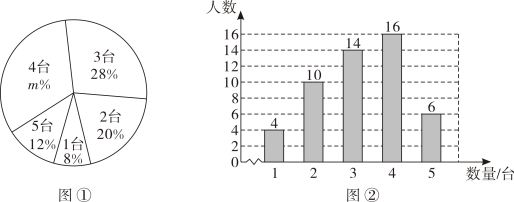
请根据相关信息,解答下列问题:
(1)、本次接受调查的学生人数为 , 图①中的值为;(2)、求统计的这组数据的平均数、众数和中位数.22. 已知一次函数( , 为常数,)的图象经过点 , .(1)、求该一次函数的解析式;(2)、当时,求该一次函数的函数值的取值范围.23. 如图,在▱ABCD中,点E,F在对角线AC上,且AE=CF.连接BE,BF,DE,DF. (1)、求证:△ABE≌△CDF;(2)、求证:四边形DEBF为平行四边形.24. 甲、乙两家商场以同样的价格出售相同的商品.“五一”节期间两家商场都举行让利酬宾活动.在甲商场按累计购物金额的收费;在乙商场累计购物金额超过200元后,超出200元的部分按收费.设在同一商场累计购物金额为元,其中 .(1)、根据题意,填写下表:
(1)、求证:△ABE≌△CDF;(2)、求证:四边形DEBF为平行四边形.24. 甲、乙两家商场以同样的价格出售相同的商品.“五一”节期间两家商场都举行让利酬宾活动.在甲商场按累计购物金额的收费;在乙商场累计购物金额超过200元后,超出200元的部分按收费.设在同一商场累计购物金额为元,其中 .(1)、根据题意,填写下表:累计购物金额/元
100
400
700
…
在甲商场实际花费/元
80
560
…
在乙商场实际花费/元
100
340
…
(2)、设在甲商场的实际花费为元,在乙商场的实际花费为元,分别写出 , 关于的函数解析式;(3)、当时,顾客在哪家商场购物的实际花费少?25. 已知直线( , 为常数,)分别与轴,轴交于点 , 点 .(1)、求该直线的解析式;(2)、若点是轴上一点,且的面积 .①求点的坐标;
②当点在轴的负半轴上时,是否存在点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,求出点的坐标;若不存在,请说明理由.