天津市和平区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 如果 $\sqrt{x - 5}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \geq 0$ B、 $x \leq 0$ C、 $x ≥ 5$ D、 $x \leq 5$

查看试题解析
2. 如图，在△ABC中，AB=8，BC=10，AC=6，则BC边上的高AD为（）

A、8 B、9 C、 $\frac{24}{5}$ D、10

查看试题解析
3. 下列判断错误的是（）

A、两组对边分别平行的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、邻边相等的平行四边形是菱形 D、两条对角线垂直且平分的四边形是正方形

查看试题解析
4. 如图，矩形ABCD的对角线交于点O，若∠ACB=30°，AB=2，则OC的长为（）

A、2 B、3 C、2 $\sqrt{3}$ D、4

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{9} = \pm 3$ C、 $3 \sqrt{2} - \frac{\sqrt{2}}{2} = \frac{5}{2} \sqrt{2}$ D、 $\sqrt{24} = 6 \sqrt{2}$

查看试题解析
6. 若一次函数 $y = k x + b$ 的图象经过第一、二、三象限，则 $k$ 、 $b$ 的取值范围是（）

A、 $k > 0$ ， $b > 0$ B、 $k > 0$ ， $b < 0$ C、 $k < 0$ ， $b < 0$ D、 $k < 0$ ， $b > 0$

查看试题解析
7. 一组数据2，2，4，3，6，5，2的众数和中位数分别是 $($ 　　 $)$

A、3，2 B、2，3 C、2，2 D、2，4

查看试题解析
8. 如图，直线 $y_{1} ＝ k x + 6$ 与直线 $y_{2} ＝ m x - 2$ 交于点P（-2，3），则关于x的不等式kx+6＞mx-2的解集是（　　）

A、x＞-2 B、x＞3 C、x＜3 D、x＜-2

查看试题解析
9. 若直角三角形的两边长分别为a、b，且满足 $\sqrt{a^{2} - 6 a + 9} + | b - 4 | = 0$ ，则该直角三角形的第三边长为（）

A、5 B、5或 $\sqrt{7}$ C、4 D、 $\sqrt{7}$ 或4

查看试题解析
10. 如图，正方形 $A B C D$ 和正方形 $C E F G$ 中，点 $D$ 在 $C G$ 上， $B C = 1$ ， $C E = 3$ ， $H$ 是 $A F$ 的中点，那么 $C H$ 的长是（）

A、 $2.5$ B、 $\sqrt{5}$ C、 $\sqrt{\frac{9}{2}}$ D、 $2$

查看试题解析
11. 如图，表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶路程随时间变化的图象．则下列结论错误的是（　　）

A、轮船的速度为20千米/时 B、快艇的速度为40千米/时 C、轮船比快艇先出发2小时 D、快艇到达乙港用了6小时

查看试题解析
12. 直线y＝x+n与直线y＝mx+3n（m是常数，m≠0且m≠1）交于点A ，当n的值发生变化时，点A到直线y＝ $\frac{3}{4}$ x-3的距离总是一个定值，则m的值是（　　）

A、3 B、2 C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析

二、填空题

13. 计算： $\sqrt{16}$ = ．

查看试题解析
14. 将直线 $y = 2 x + 3$ 向下平移5个单位长度，则平移后的直线解析式为.

查看试题解析
15. 甲、乙两人进行射击比赛，在相同条件下各射击10次，他们的平均成绩均为7环，10次射击成绩的方差分别是 $s_{甲}^{2} = 3$ ， $s_{乙}^{2} = 1.2$ ，那么成绩较为稳定的是．（填“甲”或“乙”）

查看试题解析
16. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E是AB的中点， $O E = 5 c m$ ，则AD的长为cm．

查看试题解析
17. 如图，▱ $A B C D$ 中 $∠ A = 60 °$ ， $A B = 6$ ， $A D = 2$ ， $P$ 为边 $C D$ 上一点，则 $\sqrt{3} P D + 2 P B$ 的最小值为．

查看试题解析

三、解答题

18. 如图，每个小正方形的边长都是1， $A$ ， $B$ ， $C$ ， $D$ 均在网格的格点上．

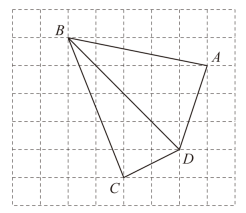(1)、判断 $∠ B C D$ 是否为直角：．（填写“是”或“不是”）

(2)、直接写出四边形 $A B C D$ 的面积为．

(3)、找到格点 $E$ ，并画出四边形 $A B E D$ （一个即可），使得其面积与四边形 $A B C D$ 面积相等．

查看试题解析
19. 计算：

(1)、 $\sqrt{18} - \sqrt{32} + \sqrt{2}$ ；

(2)、 $(2 \sqrt{3} + \sqrt{6}) (2 \sqrt{3} - \sqrt{6})$ .

查看试题解析
20. 学校为了解全校学生参加社会实践活动情况，随机调查了部分学生一学期参加社会实践活动的时间（单位：天），并用得到的数据绘制了统计图（1）和图（2）. 请根据图中提供的信息，回答下列问题：

(1)、本次随机调查的学生人数是，图（1）中m的值是；

(2)、求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数；

(3)、该校有480名学生，根据获取的社会实践活动时间样本数据，估计该校一学期社会实践活动时间大于10天的学生人数．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $∠ B = 90 ° ， A B = B C = 2 ， C D = 3 ， D A = 1$ ．

(1)、求 $∠ D A B$ 的度数；

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
22. 如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ， $A D ∥ B C$ ， $A C$ 平分 $∠ D A B$ ，连接 $B D$ 交 $A C$ 于点 $O$ ，过点 $C$ 作 $C E ⊥ A B$ 交 $A B$ 延长线于点 $E$ ．

(1)、求证：四边形 $A B C D$ 为菱形；

(2)、若 $O A = 4$ ， $O B = 3$ ，求 $C E$ 的长．

查看试题解析
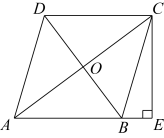23. 某地地震发生后，根据救灾指挥中心的信息，甲、乙两个重灾区急需一种大型挖掘机，甲地需要27台，乙地需要25台，A、B两省获知情况后慷慨相助，分别捐赠该型号挖掘机28台和24台，并将其全部调运往灾区，如果从A省调运一台挖掘机到甲地耗资 $0.4$ 万元，到乙地耗资 $0.3$ 万元；从B省调运一台挖掘机到甲地耗资 $0.5$ 万元，到乙地耗资 $0.2$ 万元，设从A调往甲地x台挖掘机，A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元．

(1)、用含x的代数式填写下表：

运往甲地（单位：台）
运往乙地（单位：台）
A省
          $x$
B省

运往甲地耗资（单位：万元）
运往乙地耗资（单位：万元）
A省
          $0.4 x$
B省

(2)、求y与x之间的函数关系式，并直接写出自变量x的取值范围；

(3)、若总耗资不超过 $16.2$ 万元，共有哪几种调运方案?

查看试题解析
24. 已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．

(1)、求证：△ABM≌△DCM；

(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；

(3)、当AD：AB=时，四边形MENF是正方形（只写结论，不需证明）．

查看试题解析
25. 在平面直角坐标系中，直线 $l_{1}$ ： $y = - 2 x + 6$ 与坐标轴交于 $A$ ， $B$ 两点，直线 $l_{2}$ ： $y = k x + 2 (k \neq 0)$ 与坐标轴交于点 $C$ ， $D$ ．

(1)、点 $A$ 的坐标为，点 $B$ 的坐标为；

(2)、如图，当 $k = 2$ 时，点 $C$ 的坐标为，点 $D$ 的坐标为；直线 $l_{1}$ ， $l_{2}$ 与相交于点 $E$ ，求两条直线与 $x$ 轴围成的 $△ B D E$ 的面积；

(3)、若直线 $l_{1}$ ， $l_{2}$ 与 $x$ 轴不能围成三角形， $k$ 的值为；

查看试题解析

	运往甲地（单位：台）	运往乙地（单位：台）
A省	$x$
B省
	运往甲地耗资（单位：万元）	运往乙地耗资（单位：万元）
A省	$0.4 x$
B省