安徽省亳州利辛县联考2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-09-01 类型:期末考试
一、单选题
-
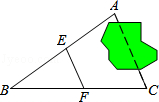
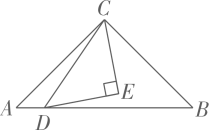
1. 如图,要测量的A、C两点被池塘隔开,李师傅在AC外任选一点B,连接BA和BC,分别取BA和BC的中点E、F,量得E、F两点间距离等于23米,则A、C两点间的距离为( )
 A、46 B、23 C、50 D、252. 下列调查中,适合用普查方式的是( )A、夏季冷饮市场上某种冰淇淋的质量 B、某品牌灯泡的使用寿命 C、某校九年级三班学生的视力 D、公民保护环境的意识3. 下列计算中,正确的是( )A、 B、 C、 D、4. “学习强国”的英语“Learningpower”中,字母“n”出现的频率是( )A、1 B、 C、 D、25. 下列运算错误的是( )A、 B、 C、 D、6. 四边形是平行四边形,下列结论中正确的是( )A、当时,它是菱形 B、当时,它是矩形 C、当时,它是正方形 D、当时,它是正方形7. 若直线y=x+1与y=-2x+a的交点在第一象限,则a的取值可以是 ( )A、-1 B、0 C、1 D、28. 某学习小组7位同学,为玉树地重灾区捐款,捐款金额分别为:5元,10元,6元,6元,7元,8元,9元,则这组数据的中位数与众数分别为( )A、6,6 B、7,6 C、7,8 D、6,89. 如图,平行四边形ABCD的对角线AC与BD相交于点O , AE⊥BC于E , AB= ,AC=2,BD=4,则AE的长为( )
A、46 B、23 C、50 D、252. 下列调查中,适合用普查方式的是( )A、夏季冷饮市场上某种冰淇淋的质量 B、某品牌灯泡的使用寿命 C、某校九年级三班学生的视力 D、公民保护环境的意识3. 下列计算中,正确的是( )A、 B、 C、 D、4. “学习强国”的英语“Learningpower”中,字母“n”出现的频率是( )A、1 B、 C、 D、25. 下列运算错误的是( )A、 B、 C、 D、6. 四边形是平行四边形,下列结论中正确的是( )A、当时,它是菱形 B、当时,它是矩形 C、当时,它是正方形 D、当时,它是正方形7. 若直线y=x+1与y=-2x+a的交点在第一象限,则a的取值可以是 ( )A、-1 B、0 C、1 D、28. 某学习小组7位同学,为玉树地重灾区捐款,捐款金额分别为:5元,10元,6元,6元,7元,8元,9元,则这组数据的中位数与众数分别为( )A、6,6 B、7,6 C、7,8 D、6,89. 如图,平行四边形ABCD的对角线AC与BD相交于点O , AE⊥BC于E , AB= ,AC=2,BD=4,则AE的长为( ) A、 B、 C、 D、10. 不等式x-1<0的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、10. 不等式x-1<0的解集在数轴上表示正确的是( )A、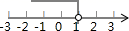 B、
B、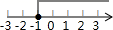 C、
C、 D、
D、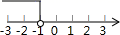
二、填空题
-
11. 若是一个完全平方式,则 .12. 若直线经过点 , 经过点 , 且与关于轴对称,则关于的不等式的解集为 .13. 花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克等于1000毫克,那么0.000037毫克可以用科学记数法表示为 .14. 如图,在等腰直角中, , , D是AB上一个动点,以DC为斜边作等腰直角 , 使点E和A位于CD两侧.点D从点A到点B的运动过程中,周长的最小值是.
 15. 在直角坐标系中,直线 与y轴交于点 ,按如图方式作正方形 、 、 …, 、 、 …在直线 上,点 、 、 …,在x轴上,图中阴影部分三角形的面积从左到右依次记为 、 、 、.. ,则 的值为 .
15. 在直角坐标系中,直线 与y轴交于点 ,按如图方式作正方形 、 、 …, 、 、 …在直线 上,点 、 、 …,在x轴上,图中阴影部分三角形的面积从左到右依次记为 、 、 、.. ,则 的值为 . 16. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同,小刚通过多次摸球试验后发现其中摸到红色,黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是 个.
16. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同,小刚通过多次摸球试验后发现其中摸到红色,黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是 个.三、解答题
-
17. 某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.(1)、求购买一个甲奖品和一个乙奖品各需多少元?(2)、经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?18. 如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF
 (1)、求证:四边形AECF是平行四边形;(2)、若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.19. 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发xmin后行走的路程为ym.图中的折线表示小亮在整个行走过程中y与x的函数关系.
(1)、求证:四边形AECF是平行四边形;(2)、若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.19. 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发xmin后行走的路程为ym.图中的折线表示小亮在整个行走过程中y与x的函数关系. (1)、小亮行走的总路程是m,他途中休息了min,休息后继续行走的速度为m/min;
(1)、小亮行走的总路程是m,他途中休息了min,休息后继续行走的速度为m/min;
(2)、当 时,求y与x的函数关系式;
(3)、当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
20. 如图,在平行四边形 中,E、F分别为边 、 的中点, 是平行四边形 的对角线, 交 的延长线于点G.
 (1)、求证:四边形 是平行四边形.(2)、若 ,求 的度数.21. 如图,在▱ABCD中,O是对角线AC的中点,AB⊥AC,BC=4cm,∠B=60°,动点P从点B出发,以2cm/s的速度沿折线BC-CD向终点D运动,连结PO并延长交折线DA-AB于点Q,设点P的运动时间为t(s).
(1)、求证:四边形 是平行四边形.(2)、若 ,求 的度数.21. 如图,在▱ABCD中,O是对角线AC的中点,AB⊥AC,BC=4cm,∠B=60°,动点P从点B出发,以2cm/s的速度沿折线BC-CD向终点D运动,连结PO并延长交折线DA-AB于点Q,设点P的运动时间为t(s). (1)、当PQ与▱ABCD的边垂直时,求PQ的长;(2)、当t取何值时,以A,P,C,Q四点组成的四边形是矩形,并说明理由;(3)、当t取何值时,CQ所在直线恰好将▱ABCD的面积分成1:3的两部分.22. 根据要求,解答下列问题.(1)、根据要求,解答下列问题.
(1)、当PQ与▱ABCD的边垂直时,求PQ的长;(2)、当t取何值时,以A,P,C,Q四点组成的四边形是矩形,并说明理由;(3)、当t取何值时,CQ所在直线恰好将▱ABCD的面积分成1:3的两部分.22. 根据要求,解答下列问题.(1)、根据要求,解答下列问题.①方程x2-2x+1=0的解为;
②方程x2-3x+2=0的解为;
③方程x2-4x+3=0的解为;
…………
(2)、根据以上方程特征及其解的特征,请猜想:①方程x2-9x+8=0的解为;
②关于x的方程的解为x1=1,x2=n.
(3)、请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.23. 在学习了正方形后,数学小组的同学对正方形进行了探究,发现: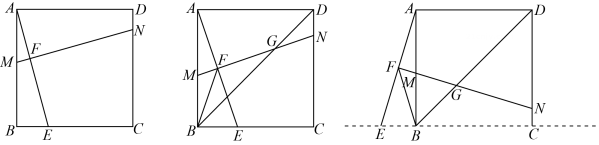
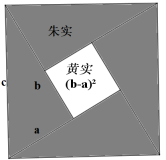
图1 图2 图3
(1)、如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE , 分别交AB、CD于点M、N . 此时,有结论AE=MN , 请进行证明;(2)、如图2,当点F为AE中点时,其他条件不变,连接正方形的对角线BD , MN 与BD交于点G , 连接BF , 此时有结论:BF= FG , 请利用图2作出证明;(3)、如图3,当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N , 请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.24. 这个图案是3世纪三国时期的赵爽在注解《周髀算经》时给出的,人们称它为赵爽弦图.赵爽根据此图指出:四个全等的直角三角形(直角边分别为a、b,斜边为c)可以如图围成一个大正方形,中间的部分是一个小正方形.请用此图证明 .