新疆乌鲁木齐市等五地2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-01 类型:期末考试
一、单选题
-
1. 函数y= 中,自变量x的取值范围是( )A、x≥1 B、x>1 C、x≥1且x≠2 D、x≠2
-
2. 下列长度的三条线段,能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,
-
3. 如图,以为直径分别向外作半圆,若 , , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4. 在ABCD中,∠ABC的平分线交AD于E,∠BED=140°,则∠A的大小为( )
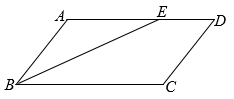 A、140° B、130° C、120° D、100°
A、140° B、130° C、120° D、100° -
5. 已知点(-3,y1)、(4,y2)在函数 y=-2x+1 图像上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定
-
6. 为了丰富校园文化,学校艺术节举行初中生书法大赛,设置了10个获奖名额.结果共有21名选手进入决赛,且决赛得分均不相同.若知道某位选手的决赛得分,要判断它是否获奖,只需知道学生决赛得分的( )A、平均数 B、中位数 C、众数 D、方差
-
7. 如图,两个高度相等且底面直径之比为的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点的距离是( ).
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
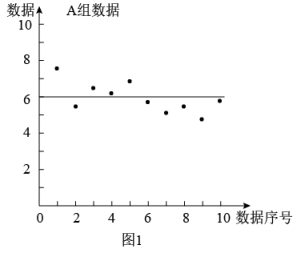
8. 把A,B两组数据分别画成下面的图1和图2,比较这两幅图,可以看出,组数据的方差较大,组数据的波动较小.

-
9. 如图,将▱ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(4,0),点C的坐标是(1,3),则点B的坐标是
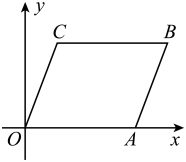
-
10. 如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AB长为半径作弧,交BC于点D,再分别以点B,D为圆心,以大于BD的长为半径作弧,两弧交于点P,作射线AP交BC于点E,如果AB=3,AC=4,那么线段AE的长度是
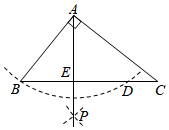
-
11. 在正方形中, , 点在边上,沿直线翻折后点落到正方形的内部点 , 连接、、 , 如图,如果 , 那么 .

-
12. 如果三角形一条边上的中线恰好等于这条边的长,那么我们称这个三角形为“匀称三角形”.在中, , 若是“匀称三角形”,那么 .
-
13. 乐乐在学习中遇到了这样的问题:
如图所示的三角形纸片中, , , , 将沿某一条直线剪开,使其变成两个三角形,且要求其中的一个三角形是等腰三角形,你有几种方法呢?

经过思考,乐乐发现要想沿一条直线把三角形分割成两个三角形,这条直线需要经过三角形的某个定点,请你帮助乐乐写出当这条直线经过点A时,剪出的等腰三角形的面积 .
三、解答题
-
14. 计算:(1)、;(2)、 .
-
15. 已知 , , 试求代数式的值.
-
16. 面临毕业季,某电脑营销商瞄准时机,在五月底筹集到资金12.12万元,用于一次性购进A、B两种型号的电脑共30台.根据市场需求,这些电脑可以全部销售,全部销售后利润不少于1.6万元,其中电脑的进价和售价见下表:
A型电脑
B型电脑
进价(元/台)
4200
3600
售价(元/台)
4800
4000
设营销商计划购进A型电脑x台,电脑全部销售后获得的利润为y元.
(1)、试写出y与x的函数关系式;(2)、该营销商有几种购进电脑的方案可供选择?(3)、该营销商选择哪种购进电脑的方案获利最大?最大利润是多少? -
17. 如图,在菱形ABCD中,E为AB边上一点,过点E作 , 交BD于点M,交CD于点F.求证: .
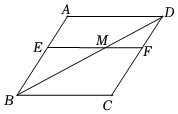
-
18. 已知点和图形 , 为图形上一点,若存在点 , 使得点为线段的中点( , 不重合),则称点为图形关于点的倍点.
如图,在平面直角坐标系中,点 , , , .
 (1)、若点的坐标为 , 则在 , , 中,是正方形关于点的倍点的是;(2)、点的坐标为 , 若在直线上存在正方形关于点的倍点,直接写出的取值范围;(3)、点为正方形边上一动点,直线与轴交于点 , 与轴交于点 , 若线段上的所有点均可成为正方形关于点的倍点,直接写出的取值范围.
(1)、若点的坐标为 , 则在 , , 中,是正方形关于点的倍点的是;(2)、点的坐标为 , 若在直线上存在正方形关于点的倍点,直接写出的取值范围;(3)、点为正方形边上一动点,直线与轴交于点 , 与轴交于点 , 若线段上的所有点均可成为正方形关于点的倍点,直接写出的取值范围. -
19. 如图,在□中,连接AC,点E是AB中点,点F是AC的中点,连接EF,过E作EG∥AF,交DA的延长线于点G.
 (1)、求证:四边形AGEF是平行四边形;(2)、若 , , , 连接GF,求GF的长.
(1)、求证:四边形AGEF是平行四边形;(2)、若 , , , 连接GF,求GF的长. -
20. 年的暑假,李刚和他的父母计划去新疆旅游,他们打算坐飞机到乌鲁木齐,第二天租用一辆汽车自驾出游.

甲公司:无固定租金,直接以租车时间计算,每天的租车费是元;
乙公司:先收取固定租金元,再按租车时间收取租金.

方案一:选择甲公司
方案二:选择乙公司
选择哪个方案合算呢?

根据以上信息,解答下列问题:
(1)、设租车时间为天,租用甲公司的车所需费用为元,租用乙公司的车所需费用为元,分别求出 , 关于的函数表达式;(2)、请你帮助李刚,选择租用哪个公司的车自驾出游比较合算,并说明理由. -
21. 在正方形ABCD中, , 点E为对角线BD上一点(不与B、D重合),且 , 连接AE,过点E作交BC于点F,请根据题意,补全图形.
 (1)、连接CE,求证::(2)、当点F恰为BC的三等分点时,求DE的长;(3)、作BG平分∠CBD交CD于点G.交EF于点H,当时,试判断AE与EH的数量关系.
(1)、连接CE,求证::(2)、当点F恰为BC的三等分点时,求DE的长;(3)、作BG平分∠CBD交CD于点G.交EF于点H,当时,试判断AE与EH的数量关系.
