天津市南开区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中x的取值范围是 $x ≥ 3$ 的是（）

A、 $\sqrt{3 - x}$ B、 $\sqrt{x - 3}$ C、 $\sqrt{3 + x}$ D、 $\frac{1}{\sqrt{x - 3}}$

查看试题解析
2. 分别以下列四组数作为三角形的边长，其中能构成直角三角形的是（）

A、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ B、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{6}$ C、2，3，4 D、6，8，10

查看试题解析
3. 函数y=3x的图象经过（）

A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限

查看试题解析
4. 如图，在正方形ABCD外侧作等边 $△ A D E$ ，则 $∠ A E B$ 的度数为（）

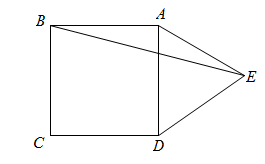A、15° B、22.5° C、20° D、10°

查看试题解析
5. 在5轮“中国汉字听写大赛”选拔赛中，甲乙两位同学的平均分都是90分，甲的成绩方差是16，乙的成绩方差是8，下列说法正确的是（）

A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定

查看试题解析
6. 下列各式的计算正确的是（）

A、 $\sqrt{\frac{- 4}{- 9}} = \frac{\sqrt{- 4}}{\sqrt{- 9}}$ B、 $\sqrt{4 \frac{2}{9}} = 2 \frac{\sqrt{2}}{3}$ C、 $\sqrt{\frac{3}{4}} = 2 \sqrt{3}$ D、 $\sqrt{\frac{3}{11}} \div \sqrt{3 \frac{2}{3}} = \sqrt{\frac{3}{11} \div \frac{11}{3}} = \frac{3}{11}$

查看试题解析
7. 一鞋店试销一种新款式鞋，试销期间卖出情况如下表：
型号
22
2.5
23
23.5
24
24.5
25
数量（双）
3
5
10
15
8
3
2
鞋店经理最关心哪种型号鞋畅销，则下列统计量对鞋店经理来说最有意义的是（）

A、平均数 B、中位数 C、众数 D、中位数或平均数

查看试题解析
8. 如图，在四边形 $A B C D$ 中， $A D ∥ B C ， A E ∥ C D$ ，且 $A E$ 交 $B C$ 于点E ， $B D$ 平分 $∠ A B C$ ．若 $A B = 3 ， B C = 7$ ，则 $B E$ 的长为（）

A、3 B、3.5 C、4 D、4.5

查看试题解析
9. 在平面直角坐标系中，直线是函数 $y = 6 x - 2$ 的图象，将直线l平移后得到直线 $y = 6 x + 2$ ，则下列平移方式正确的是（　　）

A、将l向右平移4个单位长度 B、将l向左平移4个单位长度 C、将l向上平移4个单位长度 D、将l向下平移4个单位长度

查看试题解析
10. 如图，四边形 $A B C D$ 是菱形，顶点A，C的坐标分别是 $(0 ， 2)$ ， $(8 ， 2)$ ，点D在x轴上，则顶点B的坐标是（）

A、 $(4 ， 2)$ B、 $(5 ， 2)$ C、 $(4 ， 4)$ D、 $(5 ， 4)$

查看试题解析
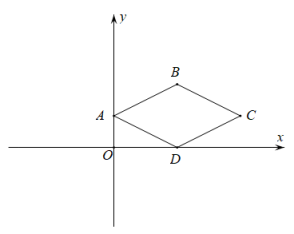11. 已知张强家、体育场、文具店在同一直线上．给出的图象反映的过程是：张强从家跑步去体育场，在体育场锻炼了若干分钟后又走到文具店去买笔，然后散步走回家．图中x表示张强离开家的时间（单位：min），y表示张强离开家的距离（单位：km）则下列说法错误的是（）

A、体育场离文具店1km B、张强在文具店逗留了20min C、张强从文具店回家的速度是 $\frac{3}{70}$ km/min D、当 $30 \leq x \leq 45$ 时， $y = \frac{1}{15} x + \frac{9}{2}$

查看试题解析
12. 如图，已知 $▱$ $O A B C$ 的顶点A ， C分别在直线 $x = 2$ 和 $x = 5$ 上，O是坐标原点，则对角线 $O B$ 长的最小值为（）

A、9 B、8 C、7 D、6

查看试题解析

二、填空题

13. 计算 $(\sqrt{11} + \sqrt{3}) (\sqrt{11} - \sqrt{3})$ 的结果为．

查看试题解析
14. 如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B ，然后把橡皮筋的中点C向上拉升3cm到点D ，拉伸过程中满足 $C D ⊥ A B$ 于点C ，则橡皮筋被拉长了cm．

查看试题解析
15. 一次函数y=kx－3的图象经过点（-1，3），则k=

查看试题解析
16. 在平面直角坐标系中，函数 $y = a x + b$ 和 $y = c x$ 的图象如图所示，它们相交于点A ．则关于x的不等式 $(c - a) x - b < 0$ 的解集为．

查看试题解析
17. 如图，在 $△ A B C$ 中，D ， E分别是 $A B$ ， $A C$ 的中点， $A B = 10$ ， F是 $D E$ 上一点，连接 $A F$ ， $B F$ ，若 $∠ A F B = 90 °$ ， $B C = 16$ ，则 $E F$ 的长为．

查看试题解析
18. 如图，在每个小正方形的边长为1的网格中，每个小正方形的顶点叫做格点．四边形 $A B C D$ 的顶点A ， B ， C ， D和边 $C D$ 上的点E均在格点上．

(1)、线段 $A E$ 的长为；

(2)、在线段 $B C$ 上找一点M ，连接 $M E$ ，使得 $B M + D E = E M$ ．请用无刻度的直尺在如图所示的网格中，画出点M ，并简要说明点M的位置是如何找到的．（不要求证明）．

查看试题解析

三、解答题

19.

(1)、 $(\sqrt{24} + \sqrt{\frac{1}{2}}) - (\sqrt{6} + \sqrt{\frac{1}{8}})$

(2)、 ${(3 - \sqrt{5})}^{2} - \sqrt{15} \div \sqrt{5} \times 2 \sqrt{3}$

查看试题解析
20. 阳光中学为了解本校初中学生在学校号召的“积极公益”活动中周末参加公益活动的时间（单位：h）的情况，随机调查了该校的部分初中学生．根据调查结果，绘制出两幅不完整的统计图．

请根据以上信息，解答下列问题：

(1)、本次接受调查的初中学生人数为，扇形图中m的值为；

(2)、求调查的这部分学生参加公益活动时间数据的平均数、众数和中位数．

查看试题解析
21. 如图，四边形 $A B C D$ 中， $A B = 20 ， B C = 15 ， C D = 7 ， A D = 24 ， ∠ B = 90 °$ ．

(1)、求证： $∠ D = 90 °$ ；

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
22. 如图，在平行四边形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点O ， $A D ⊥ B D$ 于点D ， $∠ A O D = 60 °$ ．点M ，点N分别是 $O A ， O C$ 的中点，连接 $D M ， M B ， B N ， N D$ ．

(1)、求证：四边形 $M B N D$ 为矩形；

(2)、若 $D M = 1$ ，求平行四边形 $A B C D$ 的周长．

查看试题解析
23. 为全面推进乡村振兴，某地将农户种植的农产品包装成A ， B两种大礼包．一超市预购进两种大礼包共400个，A种大礼包的进价为47元/个，预售价为65元/个；B种大礼包的进价为37元/个，预售价为50元/个．设购进A种大礼包x个，两种大礼包全部售完时获得的总利润为W元，其中x为正整数．

(1)、填表：
购进A种大礼包数量（个）
购进B种大礼包数量（个）
购进两种大礼包的总费用（元）
总利润W（元）
50
350
15300
5450
300
6700

$400 - x$

(2)、如果购进两种大礼包的总费用不超过18000元，那么商场购买两种大礼包分别为多少个时，才能获得最大利润？最大利润是多少？

查看试题解析
24. 将一个矩形纸片 $O A B C$ 放置于平面直角坐标系中，点O $(0 ， 0)$ ，点B $(10 ， 6)$ ，点A在x轴，点C在y轴．在 $A B$ 边上取一点D ，将 $△ C B D$ 沿 $C D$ 翻折，点B恰好落在边 $O A$ 上的点E处．

(1)、如图1，求点E坐标和直线 $C E$ 的解析式；

(2)、点P为x轴正半轴上的动点，设 $O P = t$ ．
①如图2，当点P在线段 $O A$ （不包含端点A ， O）上运动时，过点P作直线l $∥$ y轴，直线l被 $△ C E D$ 截得的线段长为d ．求d关于t的函数关系式，并直接写出自变量t的取值范围；

②在该坐标系所在平面内找一点G ，使以点C ， E ， P ， G为顶点的四边形为菱形，请直接写出点G的坐标．

查看试题解析

购进A种大礼包数量（个）	购进B种大礼包数量（个）	购进两种大礼包的总费用（元）	总利润W（元）
50	350	15300	5450
300			6700
	$400 - x$

型号	22	2.5	23	23.5	24	24.5	25
数量（双）	3	5	10	15	8	3	2