安徽省芜湖十一中分校2022-2023学年九年级上学期开学数学试卷
试卷更新日期:2023-09-01 类型:开学考试
一、单选题
-
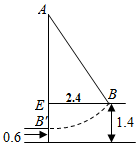
1. 要使式子 有意义,则m的取值范围是( )A、m>﹣1 B、m≥﹣1 C、m>﹣1且m≠1 D、m≥﹣1且m≠12. 下列计算正确的是( )A、 B、 C、 D、3. 下列函数中,一次函数为( )A、y=x3 B、y=﹣2x+1 C、y= D、y=2x2+14. 已知一组数据 , , , , , , , , , , 那么是这组数据的( )A、众数 B、中位数 C、平均数 D、方差5. 在四边形ABCD中,∠A+∠C=160°,∠B比∠D大60°,则∠B为( )A、70° B、80° C、120° D、130°6. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
 A、0.7米 B、1.5米 C、2.2米 D、2.4米7. 顺次连接四边形各边中点 , , , , 如果四边形是矩形,那么四边形的对角线和一定满足的关系是( )A、互相平分 B、相等 C、互相垂直 D、互相垂直平分8. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-kx+k的图象大致是( )A、
A、0.7米 B、1.5米 C、2.2米 D、2.4米7. 顺次连接四边形各边中点 , , , , 如果四边形是矩形,那么四边形的对角线和一定满足的关系是( )A、互相平分 B、相等 C、互相垂直 D、互相垂直平分8. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-kx+k的图象大致是( )A、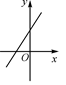 B、
B、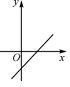 C、
C、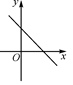 D、
D、 9. 如图,长方体的长为 , 宽为 , 高为 , 点离点的距离为 , 一只蚂蚁如果要沿着长方体的表面从点爬到点 , 需要爬行的最短距离是( )
9. 如图,长方体的长为 , 宽为 , 高为 , 点离点的距离为 , 一只蚂蚁如果要沿着长方体的表面从点爬到点 , 需要爬行的最短距离是( )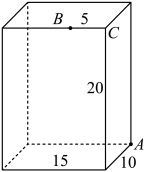 A、 B、 C、 D、10. 如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A、 B、 C、 D、10. 如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )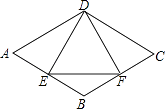 A、3 B、4 C、1 D、2
A、3 B、4 C、1 D、2二、填空题
-
11. 如果最简二次根式 与 是同类二次根式,那么a=.12. 已知函数f(x)= ,则f( )= .13. 若一个三角形三条高的交点在这个三角形的顶点上,则这个三角形是三角形.14. 如图, , 矩形的顶点B,C分别是两边上的动点,已知 , , 请完成下列探究:
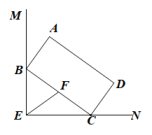 (1)、若点F是的中点,那么;(2)、点D,点E两点之间距离的最大值是 .
(1)、若点F是的中点,那么;(2)、点D,点E两点之间距离的最大值是 .三、解答题
-
15. 计算: .16. 已知a,b,c为三角形ABC的三边,且满足 ,试判断三角形ABC的形状.17. 如图,小慧和她的同学荡秋千,秋千在静止位置时,下端离地面 , 荡秋千到的位置时,下端距静止位置的水平距离等于 , 距地面 , 求秋千的长.
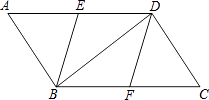
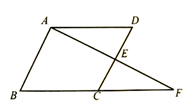
 18. 已知:如图,AD//BC,E为AF的中点,C为BF的中点.
18. 已知:如图,AD//BC,E为AF的中点,C为BF的中点.求证:四边形ABCD是平行四边形.
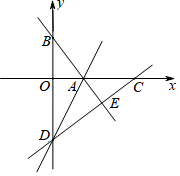
 19. 已知:一次函数y=(1﹣m)x+m﹣3(1)、若一次函数的图象过原点,求实数m的值.(2)、当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.20. 某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元。(1)、第一批饮料进货单价多少元?(2)、若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?21. 为了解防疫知识宣传教育活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分,得分均为不小于60的整数),并将测试成绩分为四个等级:基本合格(),合格(),良好(),优秀(),制作了如图统计图(部分信息未给出)由图中给出的信息解答下列问题:
19. 已知:一次函数y=(1﹣m)x+m﹣3(1)、若一次函数的图象过原点,求实数m的值.(2)、当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.20. 某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元。(1)、第一批饮料进货单价多少元?(2)、若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?21. 为了解防疫知识宣传教育活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分,得分均为不小于60的整数),并将测试成绩分为四个等级:基本合格(),合格(),良好(),优秀(),制作了如图统计图(部分信息未给出)由图中给出的信息解答下列问题: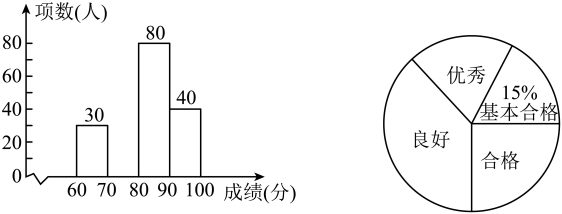 (1)、求测试成绩为合格的学生人数,并补全频数分布直方图;(2)、这次测试成绩的中位数是什么等级?(3)、请你根据抽样测试的结果估计该校获得优秀的学生有多少人.
(1)、求测试成绩为合格的学生人数,并补全频数分布直方图;(2)、这次测试成绩的中位数是什么等级?(3)、请你根据抽样测试的结果估计该校获得优秀的学生有多少人.