安徽省三海学地教育联盟2022-2023学年九年级上学期开年测数学试题
试卷更新日期:2023-09-01 类型:开学考试
一、单选题
-
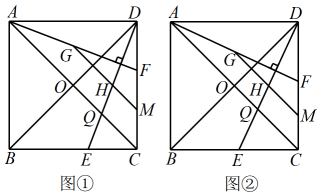
1. 下列实数中,最小的数是( )A、 B、 C、1 D、2. 据统计,安徽省2023年硕士研究生考试报名人数为人,其中用科学记数法表示为( )A、 B、 C、 D、3. 已知 , 则a的值是( )A、 B、 C、0 D、4. 2022年北京冬奥会的火炬写有全世界名字的正六边形雪花引导牌(如图①共同构成的.如图②是其中一片雪花引导牌,已知点是正六边形的边 , 的延长线的交点,则( )
 A、 B、 C、 D、5. 小明早上8点从家骑车去图书馆,计划在上午11点30分到达图书馆.出发半小时后,小明发现若原速骑行,将迟到10分钟,于是他加速继续骑行,平均每小时多骑行1千米,恰好准时到达,则小明原来的速度是( )A、12千米/小时 B、17千米/小时 C、18千米/小时 D、20千米/小时6. 如图是由16个边长为1的小正方形组成的图形,已经有3个小正方形被涂色,在涂色一个小正方形,使它和已知阴影部分组成一个轴对称图形的概率是( )
A、 B、 C、 D、5. 小明早上8点从家骑车去图书馆,计划在上午11点30分到达图书馆.出发半小时后,小明发现若原速骑行,将迟到10分钟,于是他加速继续骑行,平均每小时多骑行1千米,恰好准时到达,则小明原来的速度是( )A、12千米/小时 B、17千米/小时 C、18千米/小时 D、20千米/小时6. 如图是由16个边长为1的小正方形组成的图形,已经有3个小正方形被涂色,在涂色一个小正方形,使它和已知阴影部分组成一个轴对称图形的概率是( ) A、 B、 C、 D、7. 如图,在平行四边形中,E为边上的点,若 , 交于F,则等于( )
A、 B、 C、 D、7. 如图,在平行四边形中,E为边上的点,若 , 交于F,则等于( )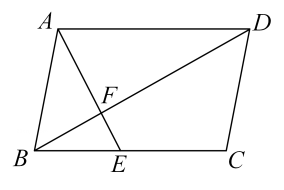 A、1:9 B、9:61 C、9:110 D、7:498. 已知实数满足 , 且 , , 若 , 则的取值范围为( )A、 B、 C、 D、9. 如图,已知点均在上,为的直径,弦的延长线与弦的延长线交于点 , 连接 . 则下列命题为假命题的是( )
A、1:9 B、9:61 C、9:110 D、7:498. 已知实数满足 , 且 , , 若 , 则的取值范围为( )A、 B、 C、 D、9. 如图,已知点均在上,为的直径,弦的延长线与弦的延长线交于点 , 连接 . 则下列命题为假命题的是( )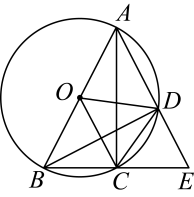 A、若点是的中点,则 B、若 , 则 C、若 , 则 D、若半径平分弦 , 则四边形是平行四边形10. 如图,在矩形中, , , 点从点出发,以每秒1个单位的速度沿着运动,同时点从点出发,以每秒2个单位的速度沿着运动,其中一点到达终点,另一点也停止运动,设 , 时间为 , 则与之间的函数图象大致为
A、若点是的中点,则 B、若 , 则 C、若 , 则 D、若半径平分弦 , 则四边形是平行四边形10. 如图,在矩形中, , , 点从点出发,以每秒1个单位的速度沿着运动,同时点从点出发,以每秒2个单位的速度沿着运动,其中一点到达终点,另一点也停止运动,设 , 时间为 , 则与之间的函数图象大致为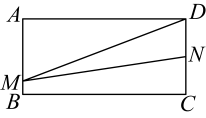 A、
A、 B、
B、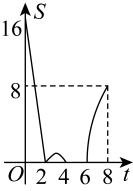 C、
C、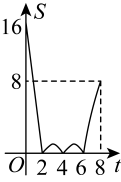 D、
D、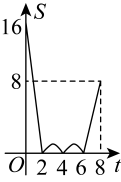
二、填空题
-
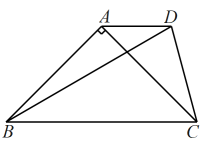
11. 在平面直角坐标系中,为坐标原点,点 , 点 , , , , 且满足 . 若的面积为 , 则的值为 (在算出的结果内任选一个).12. 如图,在梯形中, , 且 , , 则 .
 13. 双曲线和如图所示,点是上一点,分别过点作轴,轴,垂足分别为点、点 , 与分别交于点、点 , 若四边形的面积为4,则的值为 .
13. 双曲线和如图所示,点是上一点,分别过点作轴,轴,垂足分别为点、点 , 与分别交于点、点 , 若四边形的面积为4,则的值为 .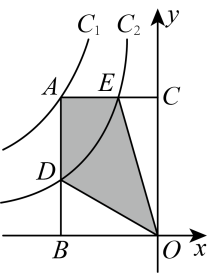 14. 已知抛物线经过点 .(1)、和的代数关系为;(2)、若 , 过点作直线轴,与轴交于点 , 与抛物线交于另一点 , , 点为直线上方抛物线上一点,求点到直线距离的最大值为 .
14. 已知抛物线经过点 .(1)、和的代数关系为;(2)、若 , 过点作直线轴,与轴交于点 , 与抛物线交于另一点 , , 点为直线上方抛物线上一点,求点到直线距离的最大值为 .三、解答题
-
15. 解方程: .16. 我国古代数学著作《九章算术》中记载以下问题:今有凫起南海,七日至北海;雁起北海,九日至南海,今凫雁俱起,问何日相逢?意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海,野鸭与大雁从南海和北海同时起飞,经过几天相遇?请解决上述问题.17. 观察以下等式:
第1个等式:;第2个等式:;
第3个等式:;第4个等式:;
按照以上规律,解决下列问题:
(1)、写出第5个等式:;(2)、写出你猜想的第个等式: ▲ (用含的等式表示),并证明.18. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点(顶点是网格线的交点).
⑴以点为位似中心,在网格中画出 , 使与的位似比为;
⑵将向右平移7格,再向下平移2格,得到 , 画出;
⑶借助网格,在上选一点 , 使得平分的面积(保留确定关键点的画法),画出线段 .
19. 如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作为的整数).反比例函数的图象为曲线 .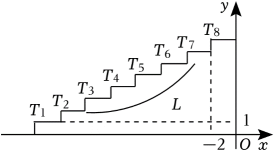 (1)、若过点 , 求反比例函数的解析式;(2)、若过点 , 则它必定还过另一点 , 求的坐标;(3)、若曲线使得这些点分布在它的两侧,每侧各4个点,求出所有满足条件的整数 .20. 如图①,中国古代的马车已经涉及很复杂的机械设计(相对当时的生产力),包含大量零部件和工艺,所彰显的智慧让人拜服,如图②是马车的侧面示意图,为车轮的直径,过圆心的车架一端点着地时,地面与车轮相切于点 , 连接 .
(1)、若过点 , 求反比例函数的解析式;(2)、若过点 , 则它必定还过另一点 , 求的坐标;(3)、若曲线使得这些点分布在它的两侧,每侧各4个点,求出所有满足条件的整数 .20. 如图①,中国古代的马车已经涉及很复杂的机械设计(相对当时的生产力),包含大量零部件和工艺,所彰显的智慧让人拜服,如图②是马车的侧面示意图,为车轮的直径,过圆心的车架一端点着地时,地面与车轮相切于点 , 连接 . (1)、徽徽猜想 , 徽徽的猜想正确吗?请说明理由;(2)、若 , 米,求车轮的直径的长.21. 安徽省淮南市曹庵镇盛产草莓,有“中国草莓第一镇”之称,这里栽培草莓已有20多年的历史.曹庵草莓又好看又好吃,它长得如鸡心,红似玛瑙,果肉细腻多汁,而其苹果酸、柠檬酸、维生素,以及胡萝卜素、钙、磷、铁的含量也比苹果、梨、葡萄高倍,营养价值很高,被人们誉为“水果皇后”.果农老蜀种植了4亩草莓,恰逢市里有农产品大赛,老蜀计划从果农里随机摘下20枚草莓查看草莓的品质.
(1)、徽徽猜想 , 徽徽的猜想正确吗?请说明理由;(2)、若 , 米,求车轮的直径的长.21. 安徽省淮南市曹庵镇盛产草莓,有“中国草莓第一镇”之称,这里栽培草莓已有20多年的历史.曹庵草莓又好看又好吃,它长得如鸡心,红似玛瑙,果肉细腻多汁,而其苹果酸、柠檬酸、维生素,以及胡萝卜素、钙、磷、铁的含量也比苹果、梨、葡萄高倍,营养价值很高,被人们誉为“水果皇后”.果农老蜀种植了4亩草莓,恰逢市里有农产品大赛,老蜀计划从果农里随机摘下20枚草莓查看草莓的品质.【收集数据】测得实际质量(单位:如下:
42,41,21,36,30,30,31,36,33,38,32,32,30,36,41,35,32,31,31,32.
【整理数据】整理以上数据,得到如下不完整的每枚质量的频数分布表:
1
3
4
3
【分析数据】根据以上数据,得到以下统计量:
统计量
平均数
中位数
方差
数据
根据以上信息,回答下列问题:
(1)、表格中的 , ;(2)、规定:若草莓的质量大于枚且不高于枚,则视为优品,此外都视为非优品.求本次采摘的优品率;(3)、已知优品比非优品每千克贵元,一次采摘的质量为 , 请估计这批货中的优品比相同质量的非优品可多卖多少元?