黑龙江省齐齐哈尔市铁锋区2022-2023学年七年级(下)期末数学试卷
试卷更新日期:2023-09-01 类型:期末考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列四个数中,属于无理数的是( )A、 B、 C、 D、2. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列调查中适合普查全面调查的是( )A、检测某城市空气质量 B、调查电视台典籍里的中国收视率 C、调查一沓钞票中有没有假钞 D、调查某批次汽车的抗撞击能力4. 如图,直线AB,CD相交于点O,OE⊥AB,∠BOD=20°,则∠COE等于( )
 A、70° B、60° C、40° D、20°5. 若 , 则下列式子一定成立的是( )A、 B、 C、 D、6. 已知点与点在同一条平行轴的直线上,且点到轴的矩离等于 , 则点的坐标是( )A、 B、或 C、 D、或7. 五一小长假,小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为( )A、30 B、26 C、24 D、228. 下列命题是假命题的是( )A、坐标平面内的点与有序实数对是一一对应的 B、算术平方根等于本身的数是和 C、同位角的平分线互相平行 D、在同一平面内,过一点有且只有一条直线与已知直线垂直9. 如图,将长方形纸片沿折叠后,点、分别落在的位置,再沿边将折叠到处,已知 , 则的度数为( )
A、70° B、60° C、40° D、20°5. 若 , 则下列式子一定成立的是( )A、 B、 C、 D、6. 已知点与点在同一条平行轴的直线上,且点到轴的矩离等于 , 则点的坐标是( )A、 B、或 C、 D、或7. 五一小长假,小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为( )A、30 B、26 C、24 D、228. 下列命题是假命题的是( )A、坐标平面内的点与有序实数对是一一对应的 B、算术平方根等于本身的数是和 C、同位角的平分线互相平行 D、在同一平面内,过一点有且只有一条直线与已知直线垂直9. 如图,将长方形纸片沿折叠后,点、分别落在的位置,再沿边将折叠到处,已知 , 则的度数为( )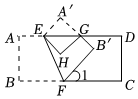 A、 B、 C、 D、10. 为落实“双减”政策,刘老师把班级里名学生分成若干小组进行小组互助学习,每个小组只能为人或人,则分组方案有( )A、种 B、种 C、种 D、种
A、 B、 C、 D、10. 为落实“双减”政策,刘老师把班级里名学生分成若干小组进行小组互助学习,每个小组只能为人或人,则分组方案有( )A、种 B、种 C、种 D、种二、填空题(本大题共7小题,共21.0分)
-
11. 的平方根为 .12. 若是二元一次方程的一个解,则的值为 .13. 若是关于的一元一次不等式,则的值为 .14. 为了估计鱼塘有多少条鱼,我们从塘里先捕上条鱼做上标记,再放回塘里,过了一段时间,待带有标记的鱼完全混合于鱼群后,第二次捕上条鱼,发现有条鱼带有标记,则估计塘里有条鱼.15. 若的两边一边互相平行,另一边互相垂直,且 , 则 .16. 若关于的不等式组无解,则的取值范围是 .17. 如图,一个机器人从点出发,向正西方向走个单位长度到达点;再向正北方向走个单位长度到达点;再向正东方向走个单位长度到达点;再向正南方向走个单位长度到达点;再向正西方向走个单位长度到达点 , 按如此规律走下去,当机器人走到点时,点的坐标为 .

三、解答题(本大题共7小题,共49.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 计算: .19.(1)、解方程组;(2)、解不等式组 , 并写出它的所有整数解.20. 如图,已知 , , , .
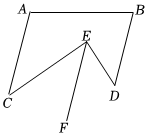 (1)、判断与的位置关系,并说明理由;(2)、若 , 求 , 的度数.21. 列方程(组)或不等式(组)解应用题:学校为了支持体育社团开展活动,鼓励同学们加强锻炼,准备增购一些羽毛球拍和乒乓球拍.
(1)、判断与的位置关系,并说明理由;(2)、若 , 求 , 的度数.21. 列方程(组)或不等式(组)解应用题:学校为了支持体育社团开展活动,鼓励同学们加强锻炼,准备增购一些羽毛球拍和乒乓球拍.
 (1)、根据图中信息,求出每支羽毛球拍和每支乒乓球拍的价格;(2)、学校准备用5300元购买羽毛球拍和乒乓球拍,且乒乓球拍的数量为羽毛球拍数量的3倍,请问最多能购买多少支羽毛球拍?22. 羊城书香浓郁,某校为进一步提升学生阅读水平,组织学生参加阅读大赛.从中抽取部分学生阅读大赛的成绩得分取正整数,满分为分进行统计分析,请根据下列尚未完成的统计图表,解答问题.
(1)、根据图中信息,求出每支羽毛球拍和每支乒乓球拍的价格;(2)、学校准备用5300元购买羽毛球拍和乒乓球拍,且乒乓球拍的数量为羽毛球拍数量的3倍,请问最多能购买多少支羽毛球拍?22. 羊城书香浓郁,某校为进一步提升学生阅读水平,组织学生参加阅读大赛.从中抽取部分学生阅读大赛的成绩得分取正整数,满分为分进行统计分析,请根据下列尚未完成的统计图表,解答问题.
组别
分数段
频数
频率
一
二
三
四
五
(1)、本次抽样调查的样本容量为 ▲ , 表中 ▲ , 并补全频数分布直方图;(2)、若把各组的分数段所占的百分比绘制成扇形统计图,则第三组对应的扇形圆心角的度数是;(3)、该校一共组织名学生参加阅读大赛,若抽取的样本具有较好的代表性,且成绩超过分为优秀,请估计该校学生中阅读能力优秀的约有多少人?23. 综合与实践如图,直线 , 直线与 , 分别交于点 , , 将一个含角的直角三角板按如图放置,使点 , 分别在直线 , 上, , , .
 (1)、的度数为 ;(2)、若的平分线交直线于点 , 如图 .
(1)、的度数为 ;(2)、若的平分线交直线于点 , 如图 .当 , 时,求的度数;
将三角板保持并向左平移,求在平移的过程中 ▲ 用含的式子表示 .
24. 综合与探究: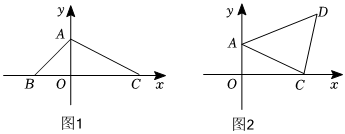
如图 , 在平面直角坐标系中,为原点,点、在坐标轴上,其中 , 、满足将点向右平移个单位长度,再向上平移个单位长度,得到对应点 , 如图所示.
(1)、点的坐标为 ,点的坐标为 ,点的坐标为 .(2)、写出点的坐标,并求出的面积;(3)、点是坐标平面内一点,若 , 请直接写出点的坐标.