【备考2024】2023年高考数学新高考一卷真题变式分层精准练：第21题

试卷更新日期：2023-09-01 类型：二轮复习

进入出卷网下载

一、原题

1. 甲乙两人投篮，每次由其中一人投篮，规则如下：若命中则此人继续投篮，若未命中则换为对方投篮.无论之前投篮情况如何，甲每次投篮的命中率均为0.6，乙每次投篮的命中率均为0.8，由抽签决定第一次投篮的人选，第一次投篮的人是甲，乙的概率各为0.5.

(1)、求第2次投篮的人是乙的概率；

(2)、求第i次投篮的人是甲的概率；

(3)、已知：若随机变量 $X_{i}$ 服从两点分布，且 $P (X_{i} = 1) = 1 - P (X_{i} = 0) = q_{i} ， i =$ $1 ， 2 ， ⋯ ， n$ ，则 $E (\sum_{i = 1}^{n} X_{i}) = \sum_{i = 1}^{n} q_{i}$ ，记前 $n$ 次 (即从第1次到第 $n$ 次投篮)中甲投篮的次数为 $Y$ ，求 $E (Y)$ .

查看试题解析

二、基础

2. 今年年初，我市某医院计划从3名医生、5名护士中随机选派4人参加湖北新冠肺炎疫情狙击战.

(1)、求选派的4人中至少有2名医生的概率；

(2)、设选派的4人中医生人数为X，求X的概率分布和数学期望.

查看试题解析

3. 2019年10月，工信部颁发了国内首个

5 G

无线电通信设备进网许可证，标志着

5 G

基站设备将正式接入公用电信商用网络.某

4 G

手机生产商拟升级设备生产

5 G

手机，有两种方案可供选择，方案1：直接引进

5 G

手机生产设备；方案2：对已有的

4 G

手机生产设备进行技术改造，升级到

5 G

手机生产设备.该生产商对未来

5 G

手机销售市场行情及回报率进行大数据模拟，得到如下统计表：

市场销售状态		畅销	平销	滞销
市场销售状态概率		$2 p$	$1 - 3 p$	$p$
预期年利润数值（单位：亿元）	方案1	70	40	-40
预期年利润数值（单位：亿元）	方案2	60	30	-10

(1)、以预期年利润的期望值为依据，求

p

的取值范围，讨论该生产商应该选择哪种方案进行设备升级？

(2)、设该生产商升级设备后生产的

5 G

手机年产量为

x

万部，通过大数据模拟核算，选择方案1所生产的

5 G

手机年度总成本

y_{1} = 0.0002 x^{2} + 0.2 x + 50

（亿元），选择方案2所生产的

5 G

手机年度总成为

y_{2} = 0.0001 x^{2} + 0.1 x + 60

（亿元）.已知

p = 0.2

，当所生产的

5 G

手机市场行情为畅销、平销和滞销时，每部手机销售单价分别为0.8万元，

0.8 - 0.001 x

（万元），

0.8 - 0.002 x

（万元），根据（1）的决策，求该生产商所生产的

5 G

手机年利润期望的最大值？并判断这个年利润期望的最大值能否达到预期年利润数值.

查看试题解析

4. 某单位组织开展“学习强国”的学习活动，活动第一周甲、乙两个部门员工的学习情况统计如下：

学习活跃的员工人数

学习不活跃的员工人数

甲

18

12

乙

32

8

参考公式： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .

参考数据： $P (K^{2} \geq 0.1) = 2.706$ ， $P (K^{2} \geq 0.05) = 3.841$ ， $P (K^{2} \geq 0.01) = 6.635$ .

(1)、根据表中数据判断能否有95%的把握认为员工学习是否活跃与部门有关；

(2)、活动第二周，单位为检查学习情况，从乙部门随机抽取2人，发现这两人学习都不活跃，能否认为乙部门第二周学习的活跃率比第一周降低了？说明理由.

查看试题解析
5. 有编号为1，2，3，...，18，19，20的20个箱子，第一个箱子有2个黄球1个绿球，其余箱子均为2个黄球2个绿球，现从第一个箱子中取出一个球放入第二个箱子，再从第二个箱子中取出一个球放入第三个箱子，以此类推，最后从第19个箱子取出一个球放入第20个箱子，记 $p_{i}$ 为从第 $i$ 个箱子中取出黄球的概率.

(1)、求 $p_{2} ， p_{3}$ ；

(2)、求 $p_{20}$ .

查看试题解析
6. 村民把土地流转给农村经济合作社后，部分村民又成为该合作社职工.下表是某地村民成为合作社职工，再经过职业培训后，个人年收入是否超过10万元的人数抽样统计：

年收入超过10万元
年收入不超过10万元
合计
男
45
5
50
女
75
25
100
合计
120
30
150
附①参考公式： $K^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)} ， n = a + b + c + d$ .
② $K^{2}$ 检验临界值表：
$P (K^{2} \geq k_{0})$
0.10
0.010
0.001
$k_{0}$
2.706
6.635
10.828

(1)、是否有99%的把握认为经过职业培训后，合作社职工年收入超过10万元与性别有关？

(2)、根据合同工期要求，合作社要完成A，B，C三种互不影响的产品加工，拟对至少完成其中两种产品加工的职工进行奖励（每个职工都有加工这三种产品的任务），若每人完成A，B，C中任何一种产品加工任务的概率都是0.8，求某职工获奖的概率（结果精确到0.1）.

查看试题解析
7. 某班有男生27名，女生18名，用分层抽样的方法从该班中抽取5名学生去敬老院参加献爱心活动.

(1)、求从该班男生、女生中分别抽取的人数；

(2)、为协助敬老院做好卫生清扫工作，从参加活动的5名学生中随机抽取2名，求这2名学生均为女生的概率.

查看试题解析
8. 某从事智能教育技术研发的科技公司开发了一个“AI作业”项目，并且在甲、乙两个学校的高一学生中做用户测试．经过一个阶段的试用，为了解“AI作业”对学生学习的促进情况，该公司随机抽取了200名学生，对他们“向量数量积”知识点掌握情况进行调查，样本调查结果如下表：

甲校
乙校
使用AI作业
不使用AI作业
使用AI作业
不使用AI作业
基本掌握
32
28
50
30
没有掌握
8
14
12
26
用样本频率估计概率，并假设每位学生是否掌据“向量数量积”知识点相互独立．

(1)、从两校高一学生中随机抽取1人，估计该学生对“向量数量积”知识点基本掌握的概率；

(2)、从样本中没有掌握“向量数量积”知识点的学生中随机抽取2名学生，以 $ξ$ 表示这2人中使用AI作业的人数，求 $ξ$ 的分布列和数学期望；

(3)、从甲校高一学生中抽取一名使用“Al作业”的学生和一名不使用“AI作业”的学生，用“ $X = 1$ ”表示该使用“AI作业”的学生基本掌握了“向量数量积”，用“ $X = 0$ ”表示该使用“AI作业”的学生没有掌握“向量数量积”，用“ $Y = 1$ ”表示该不使用“AI作业”的学生基本掌握了“向量数量积”，用“ $Y = 0$ ”表示该不使用“AI作业”的学生没有掌握“向量数量积”．直接写出方差DX和DY的大小关系．（结论不要求证明）

查看试题解析
9. 2022年春节后，新冠肺炎的新变种奥密克戎在我国部分地区爆发．该病毒是一种人传人，不易被人们直接发现，潜伏期长且传染性极强的病毒．我们把与该病毒感染者有过密切接触的人群称为密切接触者．一旦发现感染者，社区会立即对其进行流行性病医学调查，找到其密切接触者进行隔离观察．调查发现某位感染者共有10位密切接触者，将这10位密切接触者隔离之后立即进行核酸检测．核酸检测方式既可以采用单样本检测，又可以采用“k合1检测法”．“k合1检测法”是将k个样本混合在一起检测，若混合样本只要呈阳性，则该组中各个样本再全部进行单样本检测；若混合样本呈阴性，则可认为该混合样本中每个样本都是阴性．通过病毒指标检测，每位密切按触者为阴性的概率为 $p (0 < p < 1)$ ，且每位密切接触者病毒指标是否为阴性相互独立．

(1)、现对10个样本进行单样本检测，求检测结果最多有2个样本为阳性的概率 $f (p)$ 的表达式；

(2)、若对10个样本采用“5合1检测法”进行核酸检测．
①求某个混合样本呈阳性的概率；
②设总检测次数为X，求X的分布列和数学期望 $E (X)$ ．

查看试题解析

三、提高

10. 甲、乙足球爱好者为了提高球技，两人轮流进行点球训练（每人各踢一次为一轮），在相同的条件下，每轮甲、乙两人在同一位置，一人踢球另一人扑球，甲先踢，每人踢一次球，两人有1人进球另一人不进球，进球者得1分，不进球者得 $- 1$ 分；两人都进球或都不进球，两人均得0分，设甲、乙每次踢球命中的概率均为 $\frac{1}{2}$ ，甲扑到乙踢出球的概率为 $\frac{1}{2}$ ，乙扑到甲踢出球的概率 $\frac{1}{3}$ ，且各次踢球互不影响．

(1)、经过1轮踢球，记甲的得分为X，求X的分布列及数学期望；

(2)、求经过3轮踢球累计得分后，甲得分高于乙得分的概率．

查看试题解析

11. 某校为了丰富学生课余生活，组建了足球社团．足球社团为了解学生喜欢足球是否与性别有关，随机抽取了男､女同学各100名进行调查，得到如下列联表：

	喜欢足球	不喜欢足球	合计
男生	60	40	100
女生	30	70	100
合计	90	110	200

(1)、根据小概率值

α = 0.001

的

χ^{2}

独立性检验，判断是否有

99.9 %

的把握认为该校学生喜欢足球与性别有关？

(2)、现从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门．已知男生进球的概率为

\frac{1}{2}

，女生进球的概率为

\frac{1}{3}

，每人射门一次，假设各人射门相互独立，求3人进球总次数

ξ

的分布列和均值．

附： $χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ， $n = a + b + c + d$ ．

$α$	$0.050$	$0.010$	$0.001$
$x_{α}$	$3.841$	$6.635$	$10.828$

查看试题解析

12. 某学校离三年级开学之初增加早自习，早饭在校食堂就餐人数增多，为了缓解就餐压力，学校在原有一个餐厅的基础上增加了一个餐厅，分别记做餐厅甲和餐厅乙，经过一周左右统计调研分析：前一天选择餐厅甲就餐第二天选择餐厅甲就餐的概率是 $\frac{1}{4}$ ，择餐厅乙就餐的概率为 $\frac{3}{4}$ ，前一天选择餐厅乙就餐第二天选择餐厅乙就餐的概率是 $\frac{1}{2}$ ，选择餐厅甲就餐的概率也为 $\frac{1}{2}$ ，如此往复.假设学生第一天选择餐厅甲就餐的概率是 $\frac{1}{2}$ ，择餐厅乙就餐的概率是 $\frac{1}{2}$ ，记某同学第 $n$ 天选择甲餐厅就餐的概率为 $P_{n}$ .

(1)、记某班级的3位同学第二天选择餐厅甲的人数为 $X$ ，求 $X$ 的分布列，并求 $E (X)$ ；

(2)、请写出 $P_{n} (n \in N^{*})$ 的通项公式；

查看试题解析

13. 某科技公司为确定下一年度投入某种产品的研发费，需了解年研发费x（单位：万元）对年销售量y（单位：百件）和年利润（单位：万元）的影响，现对近6年的年研发费

x_{i}

和年销售量

y_{i}

（

i = 1

，2，…，6）数据作了初步处理，得到下面的散点图及一些统计量的值.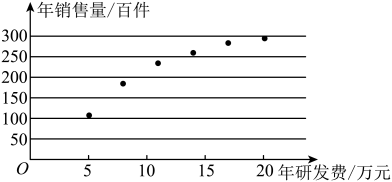

$\bar{x}$	$\bar{y}$	$\bar{μ}$	$\sum_{i = 1}^{6} {(x_{i} - \bar{x})}^{2}$	$\sum_{i = 1}^{6} {(y_{i} - \bar{y})}^{2}$	$\sum_{i = 1}^{6} {(μ_{i} - \bar{μ})}^{2}$	$\sum_{i = 1}^{6} (x_{i} - \bar{x}) (y_{i} - \bar{y})$	$\sum_{i = 1}^{6} (μ_{i} - \bar{μ}) (y_{i} - \bar{y})$
12.5	222	3.5	157.5	16800	4.5	1254	270

表中 $μ_{i} = l n x_{i}$ ， $\bar{μ} = \frac{1}{6} \sum_{i = 1}^{6} μ_{i}$ .

(1)、根据散点图判断

\hat{y} = \hat{a} + \hat{b} x

与

\hat{y} = \hat{c} + \hat{d} l n x

哪一个更适宜作为年研发费x的回归方程类型；（给出判断即可，不必说明理由）

(2)、根据（1）的判断结果及表中数据，建立y关于x的回归方程；

(3)、已知这种产品的年利润

z = 0.5 y - x

，根据（2）的结果，当年研发费为多少时，年利润z的预报值最大？附：对于一组数据

(w_{1} ， v_{1})

，

(w_{2} ， v_{2})

，…，

(w_{n} ， v_{n})

，其回归直线

\hat{v} = \hat{α} + \hat{β} w

的斜率和截距的最小二乘估计分别为

\hat{β} = \frac{\sum_{i = 1}^{n} (w_{i} - \bar{w}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(w_{i} - \bar{w})}^{2}}

，

\hat{α} = \bar{v} - \hat{β} \bar{w}

查看试题解析

14. 北京2022年冬奥会，向全世界传递了挑战自我､积极向上的体育精神，引导了健康､文明､快乐的生活方式.为了激发学生的体育运动兴趣，助力全面健康成长，某中学组织全体学生开展以“筑梦奥运，一起向未来”为主题的体育实践活动.为了解该校学生参与活动的情况，随机抽取100名学生作为样本，统计他们参加体育实践活动时间（单位：分钟），得到下表：

(1)、从该校随机抽取1名学生，若已知抽到的是女生，估计该学生参加体育实践活动时间在 $[50 ， 60)$ 的概率；

(2)、从参加体育实践活动时间在 $[80 ， 90)$ 和 $[90 ， 100)$ 的学生中各随机抽取1人，其中初中学生的人数记为X，求随机变量X的分布列和数学期望；

(3)、假设同组中每个数据用该组区间中点值代替，样本中的100名学生参加体育实践活动时间的平均数记为 $μ_{0}$ ，初中､高中学生参加体育实践活动时间的平均数分别记为 $μ_{1} ， μ_{2}$ ，当m满足什么条件时， $μ_{0} \geq \frac{μ_{1} + μ_{2}}{2}$ .（结论不要求证明）

查看试题解析
15. 随着5G商用进程的不断加快，手机厂商之间围绕5G用户的争夺越来越激烈，5G手机也频频降价飞入寻常百姓家．某科技公司为了打开市场，计划先在公司进行“抽奖免费送5G手机”优惠活动方案的内部测试，测试成功后将在全市进行推广．

(1)、公司内部测试的活动方案设置了第 $i (i \in N_{+})$ 次抽奖中奖的名额为 $3 i + 2$ ，抽中的用户退出活动，同时补充新的用户，补充新用户的名额比上一次中奖用户的名额少2个．若某次抽奖，剩余全部用户均中奖，则活动结束．参加本次内部测试第一次抽奖的有15人，甲、乙均在其中．
①请求甲在第一次中奖和乙在第二次中奖的概率分别是多少?
②请求甲参加抽奖活动次数的分布列和期望?

(2)、由于该活动方案在公司内部的测试非常顺利，现将在全市进行推广．报名参加第一次抽奖活动的有20万用户，该公司设置了第 $i (i \in N_{+})$ 次抽奖中奖的概率为 $p_{i} = \frac{9 + {(- 1)}^{i}}{40}$ ，每次中奖的用户退出活动，同时补充相同人数的新用户，抽奖活动共进行 $2 n (n \in N_{+})$ 次．已知用户丙参加了第一次抽奖，并在这 $2 n$ 次抽奖活动中中奖了，在此条件下，求证：用户丙参加抽奖活动次数的均值小于 $\frac{9}{2}$ ．

查看试题解析
16. 某学校组织“一带一路”知识竞赛，有A，B两类问题，每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误，则该同学比赛结束；若回答正确，则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束．A类问题中的每个问题回答正确得 $m (0 < m \leq 100 ， m \in N)$ 分，否则得0分；B类问题中的每个问题回答正确得 $n (0 < n \leq 100 ， n \in N)$ 分，否则得0分．已知学生甲能正确回答A类问题的概率为 $p_{1}$ ，能正确回答B类问题的概率为 $p_{2}$ ，且能正确回答问题的概率与回答次序无关．

(1)、若学生甲先回答A类问题， $m = 20$ ， $n = 80$ ， $p_{1} = 0.8$ ， $p_{2} = 0.6$ ，记X为学生甲的累计得分，求X的分布列和数学期望．

(2)、从下面的两组条件中选择一组作为已知条件．学生甲应选择先回答哪类问题，使得累计得分的数学期望最大？并证明你的结论．① $m = n$ ， $p_{1} > p_{2}$ ；② $p_{1} = p_{2}$ ， $m > n$ ．

查看试题解析
17. 某款自营生活平台以及提供配送服务的生活类软件主要提供的产品有水产海鲜，水果，蔬菜，食品，日常用品等．某机构为调查顾客对该软件的使用情况，在某地区随机访问了100人，访问结果如下表所示．

使用人数
未使用人数
女性顾客
40
20
男性顾客
20
20

(1)、从被访问的100人中随机抽取2名，求所抽取的都是女性顾客且使用该软件的概率；

(2)、用随机抽样的方法从该地区抽取10名市民，这10名市民中使用该软件的人数记为 $X$ ，问 $k (k = 0 ， 1 ， 2 ， ⋯ ， 10)$ 为何值时， $P (X = k)$ 的值最大？

查看试题解析
18. 某同学进行投篮训练，已知该同学每次投中的概率均为0.5.
附：若 $n$ 表示投篮的次数， $ξ$ 表示投中的次数，则投中的频率为 $\frac{ξ}{n}$ ；若 $η \sim N (0 ， 1)$ ，则 $P (η < 1.28) = 0.9 ， P (η < 1.645) = 0.95$ .

(1)、若该同学进行三次投篮，第一次投中得1分，第二次投中得1分，第三次投中得2分，记 $X$ 为三次总得分，求 $X$ 的分布列及数学期望；

(2)、已知当随机变量 $ξ$ 服从二项分布 $B (n ， p)$ 时，若 $n$ 充分大，则随机变量 $η = \frac{ξ - n p}{\sqrt{n p (1 - p)}}$ 服从标准正态分布 $N (0 ， 1)$ .若保证投中的频率在0.4与0.6之间的概率不低于 $90 %$ ，求该同学至少要投多少次.

查看试题解析

四、巅峰

19. 某城市响应国家号召，积极调整能源结构，推出多种价位的新能源电动汽车．根据前期市场调研，有购买新能源车需求的约有2万人，他们的选择意向统计如下：
车型
A
B
C
D
E
F
价格
9万元
12万元
18万元
24万元
30万元
40万元
占比
5%
15%
25%
35%
15%
5%

(1)、如果有购车需求的这些人今年都购买了新能源车，今年新能源车的销售额预计约为多少亿元？

(2)、车企推出两种付款方式：
全款购车：购车时一次性付款可优惠车价的3%；
分期付款：无价格优惠，购车时先付车价的一半，余下的每半年付一次，分4次付完，每次付车价的 $\frac{1}{8}$ ．
①某位顾客现有a万元现金，欲购买价值a万元的某款车，付款后剩余的资金全部用于购买半年期的理财产品（该理财产品半年期到期收益率为1.8%），到期后，可用资金（含理财收益）继续购买半年期的理财产品，问：顾客选择哪一种付款方式收益更多？（计算结果精确到0.0001）
②为了激励购买理财产品，银行对采用分期付款方式的顾客，赠送价值1888元的大礼包，试问：这一措施对哪些车型有效？（计算结果精确到0.0001）

查看试题解析

20. 中国男篮历史上曾

12

次参加亚运会，其中

8

次夺得金牌，是亚运会夺冠次数最多的球队

.

第

19

届亚运会将于

2023

年

9

月

23

日至

10

月

8

日在杭州举办．

参考公式： $K^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + d) (a + d)}$ ，其中 $n = a + b + c + d$ 为样本容量．

参考数据：

$P (K^{2} \geq k)$	$0.10$	$0.05$	$0.01$	$0.005$	$0.001$
$k$	$2.706$	$3.841$	$6.635$	$7.879$	$10.828$

(1)、为了解喜爱篮球运动是否与性别有关，某学校随机抽取了男生和女生各

100

名进行调查，得到

2 \times 2

列联表如下：

	喜爱篮球	不喜爱篮球合计
男生	$65$	$35$	$100$
女生	$25$	$75$	$100$
合计	$90$	$110$	$200$

依据小概率值 $α = 0.001$ 的独立性检验，能否认为喜爱篮球运动与性别有关？

(2)、校篮球队中的甲、乙、丙三名球员将进行传球训练，第

1

次由甲将球传出，每次传球时，传球者都等可能地将球传给另外两个人中的任何一人，如此不停地传下去，且假定每次传球都能被接到

.

记开始传球的人为第

1

次触球者，第

n

次触球者是甲的概率记为

P_{n}

，即

P_{1} = 1

．

（i）求 $P_{3}$ ， $P_{4}$ ，并证明： ${P_{n} - \frac{1}{3}}$ 为等比数列；

（ii）比较第 $15$ 次触球者是甲与第 $15$ 次触球者是乙的概率的大小．

查看试题解析

21. 为了“锤炼党性修养，筑牢党性根基”，党员教师小A每天自觉登录“学习强国APP”，参加各种学习活动，同时热衷于参与四人赛.每局四人赛是由网络随机匹配四人进行比赛，每题回答正确得20分，第1个达到100分的比赛者获得第1名，赢得该局比赛，该局比赛结束.每天的四人赛共有30局，前2局是有效局，根据得分情况获得相应名次，从而得到相应的学习积分，第1局获得第1名的得3分，获得第2、3名的得2分，获得第4名的得1分；第2局获得第1名的得2分，获得第2、3、4名的得1分；后28局是无效局，无论获得什么名次，均不能获得学习积分.经统计，小A每天在第1局四人赛中获得3分、2分、1分的概率分别为 $\frac{1}{3}$ ， $\frac{1}{2}$ ， $\frac{1}{6}$ ，在第2局四人赛中获得2分、1分的概率分别为 $\frac{1}{3}$ ， $\frac{2}{3}$ .

(1)、设小A每天获得的得分为 $X$ ，求 $X$ 的分布列、数学期望和方差；

(2)、若小A每天赛完30局，设小A在每局四人赛中获得第1名从而赢得该局比赛的概率为 $\frac{1}{3}$ ，每局是否赢得比赛相互独立，请问在每天的30局四人赛中，小A赢得多少局的比赛概率最大？

查看试题解析
22. 为了拓展学生的知识面，提高学生对航空航天科技的兴趣，培养学生良好的科学素养，某校组织学生参加航空航天科普知识答题竞赛，每位参赛学生答题若干次，答题赋分方法如下：第1次答题，答对得20分，答错得10分：从第2次答题开始，答对则获得上一次答题得分的两倍，答错得10分.学生甲参加答题竞赛，每次答对的概率为 $\frac{3}{4}$ ，各次答题结果互不影响.

(1)、求甲前3次答题得分之和为40分的概率；

(2)、记甲第i次答题所得分数 $X_{i} (i \in N^{*})$ 的数学期望为 $E (x_{i})$ .
①写出 $E (X_{i - 1})$ 与 $E (x_{i})$ 满足的等量关系式（直接写出结果，不必证明）：
②若 $E (x_{i}) > 100$ ，求i的最小值.

查看试题解析
23. 党的二十大胜利召开后，某校为调查性别因素对党史知识的了解情况是否有影响，随机抽查了男女教职工各100名，得到如下数据：

不了解
了解
女职工
30
70
男职工
20
80
附： $χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$
$α$
0.010
0.005
0.001
$x_{α}$
6.635
7.879
10.828

(1)、根据小概率值 $α = 0.005$ 的独立性检验，能否认为对党史知识的了解情况与性别有关？

(2)、为了增进全体教职工对党史知识的了解，该校组织开展党史知识竞赛活动并以支部为单位参加比赛现有两组党史题目放在甲､乙两个纸箱中，甲箱有5个选择题和3个填空题，乙箱中有4个选择题和3个填空题，比赛中要求每个支部在甲或乙两个纸箱中随机抽取两题作答.每个支部先抽取一题作答，答完后题目不放回纸箱中，再抽取第二题作答，两题答题结束后，再将这两个题目放回原纸箱中，若第一支部从甲箱中抽取了2个题目，答题结束后错将题目放入了乙箱中，接着第二支部答题，第二支部抽取第一题时，从乙箱中抽取了题目.已知第二支部从乙箱中取出的这个题目是选择题，求第一支部从甲箱中取出的是2个选择题的概率.

查看试题解析
24. 第24届冬季奥林匹克运动会（The XXIV Olympic Winter Games），即2022年北京冬季奥运会，于2022年2月4日星期五开幕，2月20日星期日闭幕．北京冬季奥运会设7个大项，15个分项，109个小项．北京赛区承办所有的冰上项目；延庆赛区承办雪车、雪橇及高山滑雪项目；张家口赛区的崇礼区承办除雪车、雪橇及高山滑雪之外的所有雪上项目．某运动队拟派出甲、乙、丙三人去参加自由式滑雪．比赛分为初赛和决赛，其中初赛有两轮，只有两轮都获胜才能进入决赛．已知甲在每轮比赛中获胜的概率均为 $\frac{3}{4}$ ；乙在第一轮和第二轮比赛中获胜的概率分别为 $\frac{4}{5}$ 和 $\frac{5}{8}$ ；丙在第一轮和第二轮获胜的概率分别是p和 $\frac{3}{2} - p$ ，其中 $0 < p < \frac{3}{4}$ ．

(1)、甲、乙、丙三人中，谁进入决赛的可能性最大；

(2)、若甲、乙、丙三人中恰有两人进入决赛的概率为 $\frac{29}{72}$ ，求p的值；

(3)、在（2）的条件下，设进入决赛的人数为 $ξ$ ，求 $ξ$ 的分布列．

查看试题解析
25. 新冠疫情在西方国家大流行，国际卫生组织对某国家进行新型冠状病毒感染率抽样调查．在某地抽取n人，每人一份血样，共 $n (n \in N^{*})$ 份，为快速有效地检验出感染过新型冠状病毒者，下面给出两种方案：
方案甲：逐份检验，需要检验n次；

方案乙：混合检验，把受检验者的血样分组，假设某组有 $k (k \in N^{*} ， k \geq 2)$ 份，分别从k份血样中取出一部分血液混合在一起检验，若检验结果为阴性，则说明这k个人全部为阴性，因而这k个人的血样只要检验这一次就够了；若检验结果为阳性，为了明确这k个人中究竟哪些人感染过新型冠状病毒，就要对这k个人的血样再逐份检验，因此这k个人的总检验次数就为 $k + 1$ ．

假设在接受检验的人中，每个人血样检验结果是阳性还是阴性是相互独立的，且每个人血样的检验结果是阳性的概率为 $p (0 < p < 1)$ ．

(1)、若 $n = 5$ ， $p = 0.2$ ，用甲方案进行检验，求5人中恰有2人感染过新型冠状病毒的概率；

(2)、记 $ζ$ 为用方案乙对k个人的血样总共需要检验的次数．
①当 $k = 5$ ， $p = 0.2$ 时，求 $E (ζ)$ ；

②从统计学的角度分析，p在什么范围内取值，用方案乙能减少总检验次数？（参考数据： ${0.8}^{4} = 0.41 ， {0.8}^{5} = 0.33 ， {0.8}^{6} = 0.26$ ）

查看试题解析
26. 某中学开展劳动实习，学生前往电子科技产业园，学习加工制造电子元件．已知学生加工出的每个电子元件正常工作的概率都是 $p (0 < p < 1)$ ，且各个电子元件正常工作的事件相互独立．现要检测 $k (k \in N^{*})$ 个这样的电子元件，并将它们串联成元件组进行筛选检测，若检测出元件组正常工作，则认为这 $k$ 个电子元件均正常工作；若检测出元件组不能正常工作，则认为这 $k$ 个电子元件中必有一个或多个电子元件不能正常工作，须再对这 $k$ 个电子元件进行逐一检测．

(1)、记对电子元件总的检测次数为 $X$ ，求 $X$ 的概率分布和数学期望；

(2)、若不对生产出的电子元件进行筛选检测，将它们随机组装进电子系统中，不考虑组装时带来的影响．已知该系统配置有 $2 n - 1 (n \in N^{*})$ 个电子元件，如果系统中有多于一半的电子元件正常工作，该系统就能正常工作．将系统正常工作的概率称为系统的可靠性，现为了改善该系统的性能，拟向系统中增加两个电子元件．记当系统配置 $2 n - 1 (n \in N^{*})$ 个电子元件时，系统正常工作的概率为 $P_{2 n - 1}$ ．我们认为当 $P_{2 n + 1} - P_{2 n - 1} > 0$ 时，增加两个电子元件提高了该系统的可靠性．
①若 $n = 1 ， p$ 满足什么条件时，增加两个电子元件能提高该系统的可靠性？

②对于 $\forall n \in N^{*} ， p$ 满足什么条件时，增加两个电子元件能提高该系统的可靠性？

查看试题解析
27. 随着互联网的快速发展和应用，越来越多的人开始选择网上购买产品和服务．某网购平台为提高2022年的销售额，组织网店开展“秒杀”抢购活动，甲，乙，丙三人计划在该购物平台分别参加 $A ， B ， C$ 三家网店各一个订单的“秒杀”抢购，已知三人在 $A ， B ， C$ 三家网店订单“秒杀”成功的概率均为 $p$ ，三人是否抢购成功互不影响．记三人抢购到的订单总数为随机变量 $Z$ ．

(1)、求 $Z$ 的分布列及 $E (Z)$ ；

(2)、已知每个订单由 $k (k \geq 2 ， k \in N^{*})$ 件商品构成，记三人抢购到的商品总数量为 $T$ ，假设 $p = \frac{1}{k} - \frac{k - 1}{2^{k}}$ ，求 $E (T)$ 取最小值时正整数 $k$ 的值．

查看试题解析
28. 已知有一道有四个选项的单项选择题和一道有四个选项的多项选择题，小明知道每道多项选择题均有两个或三个正确选项．但根据得分规则：全部选对的得5分，部分选对的得2分，有选错的得0分．这样，小明在做多项选择题时，可能选择一个选项，也可能选择两个或三个选项，但不会选择四个选项．

(1)、如果小明不知道单项选择题的正确答案，就作随机猜测．已知小明知道单项选择题的正确答案和随机猜测的概率都是 $\frac{1}{2}$ ，在他做完单项选择题后，从卷面上看，在题答对的情况下，求他知道单项选择题正确答案的概率．

(2)、假设小明在做该道多项选择题时，基于已有的解题经验，他选择一个选项的概率为 $\frac{1}{2}$ ，选择两个选项的概率为 $\frac{1}{3}$ ，选择三个选项的概率为 $\frac{1}{6}$ ．已知该道多项选择题只有两个正确选项，小明完全不知道四个选项的正误，只好根据自己的经验随机选择．记 $X$ 表示小明做完该道多项选择题后所得的分数．求：
（i） $P (X = 0)$ ；
（ii） $X$ 的分布列及数学期望．

查看试题解析
29. 2022年北京冬奥会后，由一名高山滑雪运动员甲组成的专业队，与两名高山滑雪爱好者乙、丙组成的业余队进行友谊赛．约定赛制如下：业余队中的两名队员轮流与甲进行比赛，若甲连续赢两场则专业队获胜；若甲连续输两场则业余队获胜：若比赛三场还没有决出胜负，则视为平局，比赛结束．已知各场比赛相互独立，每场比赛都分出胜负，且甲与乙比赛，乙赢概率为 $\frac{1}{3}$ ；甲与丙比赛，丙赢的概率为p，其中 $\frac{1}{3} < p < \frac{1}{2}$ ．

(1)、若第一场比赛，业余队可以安排乙与甲进行比赛，也可以安排丙与甲进行比赛．请分别计算两种安排下业余队获胜的概率；若以获胜概率大为最优决策，问：业余队第一场应该安排乙还是丙与甲进行比赛？

(2)、为了激励专业队和业余队，赛事组织规定：比赛结束时，胜队获奖金3万元，负队获奖金1.5万元；若平局，两队各获奖金1.8万元．在比赛前，已知业余队采用了（1）中的最优决策与甲进行比赛，设赛事组织预备支付的奖金金额共计X万元，求X的数学期望 $E (X)$ 的取值范围．

查看试题解析
30. 某企业对生产设备进行优化升级，升级后的设备控制系统由 $2 k - 1 (k \in N_{+})$ 个相同的元件组成，每个元件正常工作的概率均为 $p (0 < p < 1)$ ，各元件之间相互独立．当控制系统有不少于 $k$ 个元件正常工作时，设备正常运行，否则设备停止运行，记设备正常运行的概率为 $p_{k}$ （例如： $p_{2}$ 表示控制系统由3个元件组成时设备正常运行的概率； $p_{3}$ 表示控制系统由5个元件组成时设备正常运行的概率）．

(1)、若每个元件正常工作的概率 $p = \frac{2}{3}$ ．
（i）当 $k = 2$ 时，求控制系统中正常工作的元件个数 $X$ 的分布列和期望；

（ii）计算 $p_{3}$ ．

(2)、已知设备升级前，单位时间的产量为 $a$ 件，每件产品的利润为1元，设备升级后，在正常运行状态下，单位时间的产量是原来的4倍，且出现了高端产品，每件产品成为高端产品的概率为 $\frac{1}{4}$ ，每件高端产品的利润是2元．请用 $p_{k}$ 表示出设备升级后单位时间内的利润 $y$ （单位：元），在确保控制系统中元件总数为奇数的前提下，分析该设备能否通过增加控制系统中元件的个数来提高利润．

查看试题解析

	学习活跃的员工人数	学习不活跃的员工人数
甲	18	12
乙	32	8

	年收入超过10万元	年收入不超过10万元	合计
男	45	5	50
女	75	25	100
合计	120	30	150

	甲校		乙校
	使用AI作业	不使用AI作业	使用AI作业	不使用AI作业
基本掌握	32	28	50	30
没有掌握	8	14	12	26

车型	A	B	C	D	E	F
价格	9万元	12万元	18万元	24万元	30万元	40万元
占比	5%	15%	25%	35%	15%	5%

$P (K^{2} \geq k_{0})$	0.10	0.010	0.001
$k_{0}$	2.706	6.635	10.828

	使用人数	未使用人数
女性顾客	40	20
男性顾客	20	20

	不了解	了解
女职工	30	70
男职工	20	80

$α$	0.010	0.005	0.001
$x_{α}$	6.635	7.879	10.828