【备考2024】2023年高考数学新高考一卷真题变式分层精准练：第16题

试卷更新日期：2023-08-31 类型：二轮复习

进入出卷网下载

一、原题

1. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} ， F_{2}$ . 点 $A$ 在 $C$ 上. 点 $B$ 在 $y$ 轴上， $\vec{F_{1} A} ⊥ \vec{F_{1} B} ， \vec{F_{2} A} = - \frac{2}{3} \vec{F_{2} B}$ ，则 $C$ 的离心率为.

查看试题解析

二、基础

2. 双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 过点 $(\sqrt{2} ， \sqrt{3})$ ，且离心率为2，则该双曲线的标准方程为.

查看试题解析
3. 双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的渐近线的方程为 $y = \pm 2 \sqrt{2} x$ ，则该双曲线的离心率为．

查看试题解析
4. 费马定理是几何光学中的一条重要原理，在数学中可以推导出圆锥曲线的一些光学性质．例如，点P为双曲线（ $F_{1}$ ， $F_{2}$ 为焦点）上一点，点P处的切线平分 $∠ F_{1} P F_{2}$ ．已知双曲线C： $\frac{x^{2}}{4} - \frac{y^{2}}{2} = 1$ ， O为坐标原点，l是点 $P (3 ， \frac{\sqrt{10}}{2})$ 处的切线，过左焦点 $F_{1}$ 作l的垂线，垂足为M，则 $| O M | =$ ．

查看试题解析
5. 能说明“若 $m (n + 2) \neq 0$ ，则方程 $\frac{x^{2}}{m} + \frac{y^{2}}{n + 2} = 1$ 表示的曲线为椭圆或双曲线”是错误的一组 $m ， n$ 的值是.

查看试题解析
6. 已知双曲线 $\frac{x^{2}}{a^{2}} - y^{2} = 1 (a > 0)$ 的渐近线与圆 $x^{2} + y^{2} - 4 y + 3 = 0$ 相切，则 $a =$ .

查看试题解析

三、提高

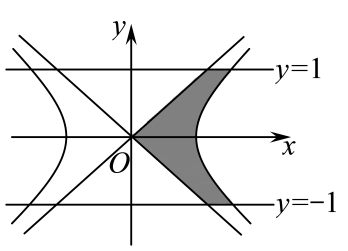
7. 已知双曲线 $Γ ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ 、 $F_{2} ， Γ$ 的渐近线与圆 $x^{2} + y^{2} = a^{2}$ 在第一象限的交点为 $M$ ，线段 $M F_{2}$ 与 $Γ$ 交于点 $N ， O$ 为坐标原点. 若 $M F_{1} / / O N$ ，则 $Γ$ 的离心率为.

查看试题解析
8. 《九章算术》中记载了我国古代数学家祖暅在计算球的体积时使用的一个原理：“幂势既同，则积不容异”，此即祖暅原理，其含义为：两个同高的几何体，如在等高处的截面的面积恒相等，则它们的体积相等.已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点到渐近线的距离记为 $d$ ，双曲线 $C$ 的两条渐近线与直线 $y = 1$ ， $y = - 1$ 以及双曲线 $C$ 的右支围成的图形（如图中阴影部分所示）绕 $y$ 轴旋转一周所得几何体的体积为 $\frac{\sqrt{6}}{3} d c π$ （其中 $c^{2} = a^{2} + b^{2}$ ），则双曲线 $C$ 的离心率为.

查看试题解析
9. 设 $F_{1} 、 F_{2}$ 为双曲线 $Γ$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{9} = 1 (a > 0)$ 左、右焦点，且 $Γ$ 的离心率为 $\sqrt{5}$ ，若点M在 $Γ$ 的右支上，直线 $F_{1} M$ 与 $Γ$ 的左支相交于点N，且 $| M F_{2} | = | M N |$ ，则 $| F_{1} N | =$ ．

查看试题解析
10. 过原点的直线 $l$ 与双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a ， b > 0)$ 的左、右两支分别交于 $M$ ， $N$ 两点， $F (2 ， 0)$ 为 $C$ 的右焦点，若 $\vec{F M} \cdot \vec{F N} = 0$ ，且 $| \vec{F M} | + | \vec{F N} | = 2 \sqrt{5}$ ，则双曲线 $C$ 的方程为.

查看试题解析
11. 设双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ ，其右焦点为 $F$ ，过 $F$ 作双曲线一条浙近线的垂线，垂足为点 $H$ ，且与另一条浙近线交于点 $Q$ ，若 $\vec{F H} = \vec{H Q}$ ，则双曲线的离心离为.

查看试题解析
12. 已知 $O$ 为坐标原点，直线 $y = x + 2$ 与双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的两条渐近线从左往右顺次交于 $A ， B$ 两点.若 $2 | O A | = | O B |$ ，则双曲线 $C$ 的离心率为.

查看试题解析
13. 已知坐标平面xOy中，点 $F_{1}$ ， $F_{2}$ 分别为双曲线 $C ： \frac{x^{2}}{a^{2}} - y^{2} = 1 (a > 0)$ 的左、右焦点，点M在双曲线C的左支上， $M F_{2}$ 与双曲线C的一条渐近线交于点D，且D为 $M F_{2}$ 的中点，点I为 $△ O M F_{2}$ 的外心，若O、I、D三点共线，则双曲线C的离心率为．

查看试题解析
14. 如图，一个光学装置由有公共焦点 $F_{1} ， F_{2}$ 的椭圆C与双曲线 $C^{'}$ 构成，一光线从左焦点 $F_{1}$ 发出，依次经过 $C^{'}$ 与C的反射，又回到点 $F_{1}$ .，历时m秒；若将装置中的 $C^{'}$ 去掉，则该光线从点 $F_{1}$ 发出，经过C两次反射后又回到点 $F_{1}$ 历时n秒，若 $C^{'}$ 的离心率为C的离心率的4倍，则 $\frac{m}{n} =$ .

查看试题解析
15. 已知 $F_{1} ， F_{2}$ 是双曲线 $C$ 的两个焦点， $P$ 为 $C$ 上一点， $∠ F_{1} P F_{2} = 6 0^{∘}$ ，且 $s i n ∠ P F_{2} F_{1} = 2 s i n ∠ P F_{1} F_{2}$ ，则 $C$ 的离心率为．

查看试题解析
16. 设双曲线 $E ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的两个焦点为 $F_{1}$ 、 $F_{2}$ ，点 $P$ 是圆 $x^{2} + y^{2} = 4 a^{2}$ 与双曲线 $E$ 的一个公共点， $∠ F_{1} P F_{2} = 60 °$ ，则该双曲线的离心率为．

查看试题解析
17. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a ， b > 0)$ 的左，右焦点分别为 $F_{1} ， F_{2}$ ，过 $F_{2}$ 且倾斜角为 $6 0^{∘}$ 的直线与双曲线右支交于 $A ， B$ 两点，若 $△ A B F_{1}$ 为等腰三角形，则该双曲线的离心率为．

查看试题解析

四、巅峰

18. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，点 $P$ 在 $C$ 的左支上， $| \vec{P F_{2}} | = 3 a$ ， $| \vec{P F_{1}} + \vec{P F_{2}} | = 2 b$ ，则 $C$ 的离心率为．

查看试题解析
19. 已知双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左，右焦点分别为 $F_{1}$ ， $F_{2}$ ，离心率为 $\frac{2 \sqrt{3}}{3}$ ，过 $F_{2}$ 作渐近线 $y = \frac{b}{a} x$ 的垂线交C于A，B两点，点A在第一象限，若 $| A F_{2} | = \frac{3 - \sqrt{3}}{2}$ ，则 $△ A B F_{1}$ 的周长为.

查看试题解析
20. 已知双曲线E： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点分别为 $F_{1}$ ， $F_{2}$ ， A为其右顶点，P为双曲线右支上一点，直线 $P F_{1}$ 与 $y$ 轴交于Q点．若 $A Q / / P F_{2}$ ，则双曲线E的离心率的取值范围为．

查看试题解析
21. 已知曲线C₁方程： $x^{2} + k y^{2} = 1 （ 2 \leq k \leq 3 ）$ ，曲线C₂方程： $t x^{2} + y^{2} = 1 （ 3 \leq t \leq 4 ）$ ，曲线C₃为焦点在x轴上的双曲线，且它的渐近线过C₁与C₂的交点，则曲线C₃的离心率的取值范围是.

查看试题解析
22. 过双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左焦点F作直线l与双曲线交于A，B两点，使得 $| A B | = 4 b$ ，若这样的直线有且仅有两条，则离心率e的取值范围是．

查看试题解析
23. 已知 $F_{1}$ ， $F_{2}$ 分别是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点， $O$ 为坐标原点，以 $F_{1} O$ 为直径的圆与双曲线的一条渐近线交于点A（A在第二象限），射线 $F_{1} A$ 与双曲线的另一条渐近线相交于点 $B$ ，满足 $S_{△ B O F_{2}} = 2 S_{△ A O F_{1}}$ ，则双曲线的离心率为．

查看试题解析
24. 已知P是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a ， b > 0)$ 上一点， $F_{1}$ ， $F_{2}$ 分别是左、右焦点，焦距为2c， $△ P F_{1} F_{2}$ 的内切圆的周长是 $π c$ ，则离心率e的取值范围是.

查看试题解析
25. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} 、 F_{2}$ ，过 $F_{2}$ 且斜率为 $- \frac{\sqrt{5}}{2}$ 的直线与双曲线C的左支交于点A．若 $(\vec{F_{1} F_{2}} + \vec{F_{1} A}) \cdot \vec{F_{2} A} = 0$ ，则双曲线C的渐近线方程为．

查看试题解析
26. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ ，其左右焦点分别为 $F_{1} (- \sqrt{7} ， 0)$ ， $F_{2} (\sqrt{7} ， 0)$ ，点P是双曲线右支上的一点，点I为 $△ P F_{1} F_{2}$ 的内心（内切圆的圆心）， $\vec{P I} = x \vec{P F_{1}} + y \vec{P F_{2}}$ ，若 $∠ F_{1} P F_{2} = 60 °$ ， $y = 3 x$ ，则 $△ P F_{1} F_{2}$ 的内切圆的半径为.

查看试题解析
27. 已知双曲线 $C ： \frac{y^{2}}{4} - \frac{x^{2}}{b^{2}} = 1 (b > 0)$ 的上顶点、下焦点分别为M，F，以M为圆心，b为半径的圆与C的一条渐近线交于A，B两点，若 $∠ A M B = 60 °$ ， AB的中点为Q（Q在第一象限），点P在双曲线的下支上，则当 $| P F | + | P Q |$ 取得最小值时，直线PQ的斜率为．

查看试题解析
28. 已知点 $P$ 在双曲线 $\frac{x^{2}}{4} - \frac{y^{2}}{5} = 1$ 的右支上， $A (0 ， 2)$ ，动点 $B$ 满足 $| A B | = 2$ ， $F$ 是双曲线的右焦点，则 $| P F | - | P B |$ 的最大值为.

查看试题解析