【备考2024】2023年高考数学新高考一卷真题变式分层精准练:第14题
试卷更新日期:2023-08-31 类型:二轮复习
一、原题
-
1. 在正四棱台 中, , 则该棱台的体积为.
二、基础
-
2. 已知正方体的棱长为2,E,F分别为棱的中点,则三棱锥的体积为.3. 如图,在正四棱台中, , 且四棱锥的体积为48,则该四棱台的体积为.
 4. 多面体的各顶点在半径为2的球面上,是矩形, , 则多面体体积的最大值为.5. 如图所示的图案,是由圆柱、球和圆锥组成,已知球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面,则图案中圆锥、球、圆柱的体积.
4. 多面体的各顶点在半径为2的球面上,是矩形, , 则多面体体积的最大值为.5. 如图所示的图案,是由圆柱、球和圆锥组成,已知球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面,则图案中圆锥、球、圆柱的体积.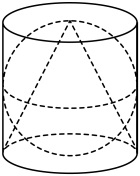
三、提高
-
6. 已知四棱锥的底面是边长为的正方形,侧棱长均为 . 若点在圆柱的一个底面圆周上,点P在圆柱的另一个底面内,则该圆柱的体积为 .7. 已知直四棱柱的棱长均为2, , 除面ABCD外,该四棱柱其余各个面的中心分别为点E,F,G,H,Ⅰ,则由点E,F,G,H,Ⅰ构成的四棱锥的体积为 .8. 在正四棱锥中,为的中点,过作截面将该四棱锥分成上、下两部分,记上、下两部分的体积分别为 , 则的最大值是.9. 在棱长为的正方体中,是底面内动点,且平面 , 当最大时,三棱锥的体积为 .10. 在正方体中,分别是棱的中点,过、、的平面把正方体截成两部分体积分别为 , 则.11. 如图为三棱锥的平面展开图,其中 , , 垂足为 , 则该三棱锥的体积为 .
 12. 如图,在四棱锥中,底面为矩形,底面 , 为棱上任意一点(不包括端点),为棱上任意一点(不包括端点),且 . 已知 , , 当三棱锥的体积取得最大值时,与底面所成角的正切值为 .
12. 如图,在四棱锥中,底面为矩形,底面 , 为棱上任意一点(不包括端点),为棱上任意一点(不包括端点),且 . 已知 , , 当三棱锥的体积取得最大值时,与底面所成角的正切值为 . 13. 正三棱锥的高为为中点,过作与棱平行的平面,将三棱锥分为上下两部分,设上、下两部分的体积分别为 , 则.
13. 正三棱锥的高为为中点,过作与棱平行的平面,将三棱锥分为上下两部分,设上、下两部分的体积分别为 , 则.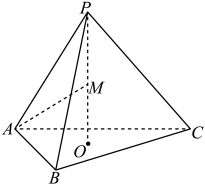
四、巅峰
-
14. 在三棱锥中, , , 则三棱锥外接球的体积与三棱锥的体积之比为.15. 在三棱锥P-ABC中, , 点M,N分别是PB,BC的中点,且 , 则平面AMN截三棱锥P-ABC的外接球所得截面的面积是 .16. 在四棱锥中,底面是正方形,底面.若四棱锥的体积为9,且其顶点均在球上,则当球的体积取得最小值时, , 此时球心到平面的距离是.17. 正四面体ABCD的棱长为3,P在棱AB上,且满足 , 记四面体ABCD的内切球为球 , 四面体PBCD的外接球为球 , 则 .18. 如图,正方体的棱长为 , 若空间中的动点满足 , , 则下列命题正确的是 . (请用正确命题的序号作答)
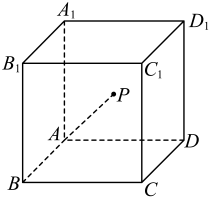
①若 , 则点到平面的距离为;
②若 , 则二面角的平面角为;
③若 , 则三棱锥的体积为;
④若 , 则点的轨迹构成的平面图形的面积为 .
19. 在棱长为1的正方体中,为底面的中心, , , 为线段的中点,则下列命题中正确的序号为.
①与共面;
②三棱锥的体积跟的取值无关;
③当时,过三点的平面截正方体所得截面的周长为;
④时,.
20. 某数学兴趣小组的学生开展数学活动,将图①所示的三块直角三角板进行拼接、旋转等变化,进而研究体积与角的问题,其中 , , 直角三角板与始终全等(假设直角三角板与的另两边的大小可变化).现将直角三角板与放在平面内拼接,直角三角板的直角边也放在平面内,并使与重合,将直角三角板绕着旋转,使点在平面内的射影始终与点重合于点 , 如图②,则当四棱锥的体积最大时,直角三角板的内角的余弦值为.
-