【备考2024】2023年高考数学新高考一卷真题变式分层精准练:第12题
试卷更新日期:2023-08-31 类型:二轮复习
一、原题
-
1. 下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有( )A、直径为0.99m的球体 B、所有棱长均为1.4m的四面体 C、底面直径为0.01m,高为1.8m的圆柱体 D、底面直径为1.2m,高为0.01m的圆柱体
二、基础
-
2. 如图所示,一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,关于圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比说法正确的是( )
 A、体积之比 B、体积之比 C、表面积之比 D、表面积之比3. 下列命题为真命题的有( )A、过直线l外一点P,存在唯一平面与直线l垂直 B、过直线l外一点P,存在唯一平面与直线l平行 C、过平面外一点P,存在唯一平面与平面垂直 D、过平面外一点P,存在唯一平面与平面平行4. 从正方体的8个顶点中任选4个不同顶点,然后将它们两两相连,可组成空间几何体.这个空间几何体可能是( )A、每个面都是直角三角形的四面体; B、每个面都是等边三角形的四面体; C、每个面都是全等的直角三角形的四面体; D、有三个面为等腰直角三角形,有一个面为等边三角形的四面体.5. 下列命题正确的是( )A、有两个面平行,其余各面都是平行四边形的几何体叫棱柱 B、棱锥是由一个底面为多边形,其余各面为具有公共顶点的三角形围成的几何体 C、用一个平面去截棱锥,棱锥底面和截面之间的部分为棱台 D、球面可以看作一个圆绕着它的直径所在的直线旋转180°所形成的曲面6. 设m,n是两条不同的直线,是两个不同的平面,下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 一个多面体的所有棱长都相等,那么这个多面体一定不可能是( )A、三棱锥 B、四棱台 C、六棱锥 D、六面体8. 在正方体中,点E为线段上的动点,则( )A、直线DE与直线AC所成角为定值 B、点E到直线AB的距离为定值 C、三棱锥的体积为定值 D、三棱锥外接球的体积为定值9. 已知正方体的棱长为分别是棱的中点,是棱上的一动点,则( )A、存在点 , 使得 B、对任意的点 C、存在点 , 使得直线与平面所成角的大小是 D、对任意的点 , 三棱锥的体积是定值10. 折扇在我国已有三四千年的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它以字画的形式集中体现了我国文化的方方面面,是运筹帷幄,决胜千里,大智大勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若扇形的两个圆弧所在圆的半径分别是1和3,且 , 则该圆台( )
A、体积之比 B、体积之比 C、表面积之比 D、表面积之比3. 下列命题为真命题的有( )A、过直线l外一点P,存在唯一平面与直线l垂直 B、过直线l外一点P,存在唯一平面与直线l平行 C、过平面外一点P,存在唯一平面与平面垂直 D、过平面外一点P,存在唯一平面与平面平行4. 从正方体的8个顶点中任选4个不同顶点,然后将它们两两相连,可组成空间几何体.这个空间几何体可能是( )A、每个面都是直角三角形的四面体; B、每个面都是等边三角形的四面体; C、每个面都是全等的直角三角形的四面体; D、有三个面为等腰直角三角形,有一个面为等边三角形的四面体.5. 下列命题正确的是( )A、有两个面平行,其余各面都是平行四边形的几何体叫棱柱 B、棱锥是由一个底面为多边形,其余各面为具有公共顶点的三角形围成的几何体 C、用一个平面去截棱锥,棱锥底面和截面之间的部分为棱台 D、球面可以看作一个圆绕着它的直径所在的直线旋转180°所形成的曲面6. 设m,n是两条不同的直线,是两个不同的平面,下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 一个多面体的所有棱长都相等,那么这个多面体一定不可能是( )A、三棱锥 B、四棱台 C、六棱锥 D、六面体8. 在正方体中,点E为线段上的动点,则( )A、直线DE与直线AC所成角为定值 B、点E到直线AB的距离为定值 C、三棱锥的体积为定值 D、三棱锥外接球的体积为定值9. 已知正方体的棱长为分别是棱的中点,是棱上的一动点,则( )A、存在点 , 使得 B、对任意的点 C、存在点 , 使得直线与平面所成角的大小是 D、对任意的点 , 三棱锥的体积是定值10. 折扇在我国已有三四千年的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它以字画的形式集中体现了我国文化的方方面面,是运筹帷幄,决胜千里,大智大勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若扇形的两个圆弧所在圆的半径分别是1和3,且 , 则该圆台( ) A、高为 B、表面积为 C、体积为 D、上底面积、下底面积和侧面积之比为11. 某一时段内,从天空降落到地面上的液态或固态的水,未经蒸发,渗透流失,而在水平面上积聚的深度称为这段时间的降雨量,降雨量的等级划分如下:
A、高为 B、表面积为 C、体积为 D、上底面积、下底面积和侧面积之比为11. 某一时段内,从天空降落到地面上的液态或固态的水,未经蒸发,渗透流失,而在水平面上积聚的深度称为这段时间的降雨量,降雨量的等级划分如下:
等级
降雨量()
小雨
中雨
大雨
暴雨
大暴雨
特大暴雨
在一次暴雨降雨过程中,小明用一个大容量烧杯(如图,瓶身直径大于瓶口直径,瓶身高度为 , 瓶口高度为)收集雨水,降雨结束后,容器内雨水的高度可能是( )
A、 B、 C、 D、三、提高
-
12. 如图,已知圆锥SO母线长l=5,底面半径r=4,则下列结论中正确的有( )
 A、圆锥的表面积为 B、圆锥侧面展开图的圆心角为 C、圆锥的体积为 D、圆锥的轴截面是锐角三角形13. 陀螺是中国民间最早的娱乐工具之一,也叫做陀罗,间南语称作“干乐”,北方叫做“冰尜(gá)”或“打老牛”。传统古陀螺大致是木制或铁制的倒圆锥形.现有一圆锥形陀螺(如图所示),其底面半径为3,将其放倒在一平面上,使圆锥在此平面内绕圆锥顶点滚动,当圆锥在平面内转回原位置时,圆锥本身恰好滚动了3周,则( )
A、圆锥的表面积为 B、圆锥侧面展开图的圆心角为 C、圆锥的体积为 D、圆锥的轴截面是锐角三角形13. 陀螺是中国民间最早的娱乐工具之一,也叫做陀罗,间南语称作“干乐”,北方叫做“冰尜(gá)”或“打老牛”。传统古陀螺大致是木制或铁制的倒圆锥形.现有一圆锥形陀螺(如图所示),其底面半径为3,将其放倒在一平面上,使圆锥在此平面内绕圆锥顶点滚动,当圆锥在平面内转回原位置时,圆锥本身恰好滚动了3周,则( ) A、圆锥的母线长为9 B、圆锥的表面积为 C、圆锥的侧面展开图(扇形)的圆心角为 D、圆锥的体积为14. 如图,圆锥底面的直径为 , : , 为的中点,则下列说法正确的有( )
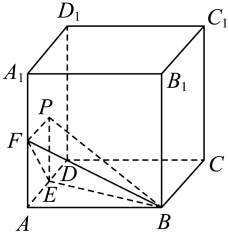
A、圆锥的母线长为9 B、圆锥的表面积为 C、圆锥的侧面展开图(扇形)的圆心角为 D、圆锥的体积为14. 如图,圆锥底面的直径为 , : , 为的中点,则下列说法正确的有( )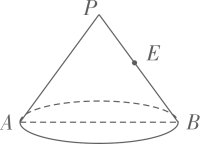 A、圆锥的体积为 B、圆锥内切球的半径为 C、过截圆锥所得截面面积最大为 D、点沿圆锥表面到的最短路经长为15. 圆锥内半径最大的球称为该圆锥的内切球,若圆锥的顶点和底面的圆周都在同一个球面上,则称该球为圆锥的外接球.如图,圆锥的内切球和外接球的球心重合,且圆锥的底面直径为 , 则( )
A、圆锥的体积为 B、圆锥内切球的半径为 C、过截圆锥所得截面面积最大为 D、点沿圆锥表面到的最短路经长为15. 圆锥内半径最大的球称为该圆锥的内切球,若圆锥的顶点和底面的圆周都在同一个球面上,则称该球为圆锥的外接球.如图,圆锥的内切球和外接球的球心重合,且圆锥的底面直径为 , 则( ) A、设内切球的半径为 , 外接球的半径为 , 则 B、设内切球的表面积 , 外接球的表面积为 , 则 C、设圆锥的体积为 , 内切球的体积为 , 则 D、设、是圆锥底面圆上的两点,且 , 则平面截内切球所得截面的面积为16. 如图,在正方体中,点P在线段上运动时,下列命题正确的是( )
A、设内切球的半径为 , 外接球的半径为 , 则 B、设内切球的表面积 , 外接球的表面积为 , 则 C、设圆锥的体积为 , 内切球的体积为 , 则 D、设、是圆锥底面圆上的两点,且 , 则平面截内切球所得截面的面积为16. 如图,在正方体中,点P在线段上运动时,下列命题正确的是( )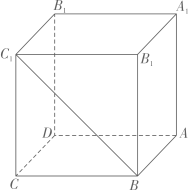 A、三棱锥的体积不变 B、直线CP与直线所成角的取值范围为 C、直线AP与平面所成角的大小不变 D、二面角的大小不变17. 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;阳马指底面为矩形,一侧棱垂直于底面的四棱锥;鳖臑指四个面均为直角三角形的四面体.如图,在堑堵中, , , 则下列说法正确的是( )
A、三棱锥的体积不变 B、直线CP与直线所成角的取值范围为 C、直线AP与平面所成角的大小不变 D、二面角的大小不变17. 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;阳马指底面为矩形,一侧棱垂直于底面的四棱锥;鳖臑指四个面均为直角三角形的四面体.如图,在堑堵中, , , 则下列说法正确的是( ) A、四棱锥为阳马 B、三棱锥为鳖臑 C、当三棱锥的体积最大时,二面角的余弦值为 D、记四棱锥的体积为 , 三棱锥的体积为 , 则18. 如图,在棱长为2的正方体中,点E为的中点,点P在线段(不包含端点)上运动,记二面角的大小为 , 二面角的大小为 , 则( )
A、四棱锥为阳马 B、三棱锥为鳖臑 C、当三棱锥的体积最大时,二面角的余弦值为 D、记四棱锥的体积为 , 三棱锥的体积为 , 则18. 如图,在棱长为2的正方体中,点E为的中点,点P在线段(不包含端点)上运动,记二面角的大小为 , 二面角的大小为 , 则( ) A、异面直线BP与AC所成角的范围是 B、的最小值为 C、当的周长最小时,三棱锥的体积为 D、用平面截正方体 , 截面的形状为梯形19. 如图,棱长为的正方体中中,下列结论正确的是( )
A、异面直线BP与AC所成角的范围是 B、的最小值为 C、当的周长最小时,三棱锥的体积为 D、用平面截正方体 , 截面的形状为梯形19. 如图,棱长为的正方体中中,下列结论正确的是( ) A、异面直线与所成的角为 B、直线与平面所成的角为 C、二面角平面角的正切值为 D、点到平面的距离为20. 圆锥内半径最大的球称为该圆锥的内切球若圆锥的顶点和底面的圆周都在同一个球面上,则称该球为圆锥的外接球如图,圆锥的内切球和外接球的球心重合,且圆锥的底面直径为 , 则( )
A、异面直线与所成的角为 B、直线与平面所成的角为 C、二面角平面角的正切值为 D、点到平面的距离为20. 圆锥内半径最大的球称为该圆锥的内切球若圆锥的顶点和底面的圆周都在同一个球面上,则称该球为圆锥的外接球如图,圆锥的内切球和外接球的球心重合,且圆锥的底面直径为 , 则( ) A、设内切球的半径为 , 外接球的半径为 , 则 B、设内切球的表面积 , 外接球的表面积为 , 则 C、设圆锥的体积为 , 内切球的体积为 , 则 D、设 , 是圆锥底面圆上的两点,且 , 则平面截内切球所得截面的面积为21. 素描几何体是素描初学者学习绘画的必学课程,是复杂形体最基本的组成和表现方式,因此几何体是美术人门最重要的一步.素描几何体包括:柱体、椎体、球体以及它们的组合体和穿插体.十字穿插体,是由两个相同的长方体相互从中部贯穿而形成的几何体,也可以看作四个相同的几何体(记为拼接而成,体现了数学的对称美.已知在如下图的十字穿插体中, , 下列说法正确的是( )
A、设内切球的半径为 , 外接球的半径为 , 则 B、设内切球的表面积 , 外接球的表面积为 , 则 C、设圆锥的体积为 , 内切球的体积为 , 则 D、设 , 是圆锥底面圆上的两点,且 , 则平面截内切球所得截面的面积为21. 素描几何体是素描初学者学习绘画的必学课程,是复杂形体最基本的组成和表现方式,因此几何体是美术人门最重要的一步.素描几何体包括:柱体、椎体、球体以及它们的组合体和穿插体.十字穿插体,是由两个相同的长方体相互从中部贯穿而形成的几何体,也可以看作四个相同的几何体(记为拼接而成,体现了数学的对称美.已知在如下图的十字穿插体中, , 下列说法正确的是( ) A、平面 B、与所成角的余弦值为 C、平面截该十字穿插体的外接球的截面面积为 D、几何体的体积为
A、平面 B、与所成角的余弦值为 C、平面截该十字穿插体的外接球的截面面积为 D、几何体的体积为四、巅峰
-
22. 已知正方体的棱长为为空间中任一点,则下列结论中正确的是( )A、若为线段上任一点,则与所成角的范围为 B、若为正方形的中心,则三棱锥外接球的体积为 C、若在正方形内部,且 , 则点轨迹的长度为 D、若三棱锥的体积为恒成立,点轨迹的为椭圆的一部分23. 已知为等腰直角三角形,为斜边且长度是 . 为等边三角形,若二面角为直二面角,则下列说法正确的是( )A、 B、三棱锥的体积为 C、三棱锥外接球的表面积为 D、半径为的球可以被整体放入以三棱锥为模型做的容器中24. 已知正四面体的棱长为分别为正四面体棱的中点,为面内任意一点,则下列结论正确的是( )A、平面截正四面体的外接球所得截面的面积为 B、若存在 , 使得 , 则线段长度的最小值为 C、过点作平面平面 , 若平面平面 , 平面平面 , 则所成角的正弦值为 D、平面与平面夹角的余弦值为25. 数学中有许多形状优美,寓意独特的几何体,“勒洛四面体”就是其中之一.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分.如图,在勒洛四面体中,正四面体的棱长为4,则下列结论正确的是( )
 A、勒洛四面体最大的截面是正三角形 B、若是勒洛四面体表面上的任意两点,则的最大值为4 C、勒洛四面体的体积是 D、勒洛四面体内切球的半径是26. 已知正方体的棱长为为空间中任一点,则下列结论中正确的是( )A、若为线段上任一点,则与所成角的余弦值范围为 B、若为正方形的中心,则三棱锥外接球的体积为 C、若在正方形内部,且 , 则点轨迹的长度为 D、若三棱锥的体积为恒成立,点轨迹的为圆的一部分27. 已知圆台的上下底面的圆周都在半径为2的球面上,圆台的下底面过球心,上底面半径为 , 设圆台的体积为V,则下列选项中说法正确的是( )A、当时, B、V存在最大值 C、当r在区间内变化时,V逐渐减小 D、当r在区间内变化时,V先增大后减小
A、勒洛四面体最大的截面是正三角形 B、若是勒洛四面体表面上的任意两点,则的最大值为4 C、勒洛四面体的体积是 D、勒洛四面体内切球的半径是26. 已知正方体的棱长为为空间中任一点,则下列结论中正确的是( )A、若为线段上任一点,则与所成角的余弦值范围为 B、若为正方形的中心,则三棱锥外接球的体积为 C、若在正方形内部,且 , 则点轨迹的长度为 D、若三棱锥的体积为恒成立,点轨迹的为圆的一部分27. 已知圆台的上下底面的圆周都在半径为2的球面上,圆台的下底面过球心,上底面半径为 , 设圆台的体积为V,则下列选项中说法正确的是( )A、当时, B、V存在最大值 C、当r在区间内变化时,V逐渐减小 D、当r在区间内变化时,V先增大后减小
-