沪科版数学八年级上册第15章轴对称图形章末过关检测卷
试卷更新日期:2023-08-31 类型:单元试卷
一、选择题(每题4分,共40分)
-
1. 下列图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 等腰三角形的一个外角是70°,则它的顶角的度数为( )A、70° B、70°或40° C、110° D、110°或40°3. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、
2. 等腰三角形的一个外角是70°,则它的顶角的度数为( )A、70° B、70°或40° C、110° D、110°或40°3. 如图,△ABC中,AB<AC<BC,如果要使用尺规作图的方法在BC上确定一点P,使PA+PB=BC,那么符合要求的作图痕迹是( )A、 B、
B、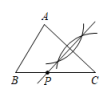 C、
C、 D、
D、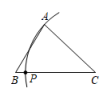 4. 已知,如图,中, , , , 的垂直平分线交于点M,交于点E,的垂直平分线交于点N,交于点F,则的长为( )
4. 已知,如图,中, , , , 的垂直平分线交于点M,交于点E,的垂直平分线交于点N,交于点F,则的长为( ) A、3cm B、4cm C、6cm D、12cm5. 如图,将纸片沿折叠,点A落在点F处,已知 , 则的度数等于( )
A、3cm B、4cm C、6cm D、12cm5. 如图,将纸片沿折叠,点A落在点F处,已知 , 则的度数等于( )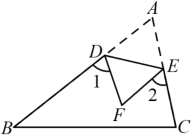 A、 B、 C、 D、6. 一副直角三角板按如图所示的方式放置,点E在边BC的延长线上, , , 则的度数为( )
A、 B、 C、 D、6. 一副直角三角板按如图所示的方式放置,点E在边BC的延长线上, , , 则的度数为( ) A、30° B、25° C、20° D、15°7. 如图,中,是高, , 则长为( )
A、30° B、25° C、20° D、15°7. 如图,中,是高, , 则长为( ) A、4 B、5 C、6 D、78. 如图,点P是内部的一点,点P到三边的距离 , , 则的度数为( )
A、4 B、5 C、6 D、78. 如图,点P是内部的一点,点P到三边的距离 , , 则的度数为( ) A、65° B、80° C、100° D、70°9. 如图所示的网格是正方形网格,点A,B,P是网格线的交点,则∠PAB+∠PBA=( )
A、65° B、80° C、100° D、70°9. 如图所示的网格是正方形网格,点A,B,P是网格线的交点,则∠PAB+∠PBA=( ) A、30° B、45° C、60° D、75°10. 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,则∠AMN+∠ANM的度数为( )
A、30° B、45° C、60° D、75°10. 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小,则∠AMN+∠ANM的度数为( )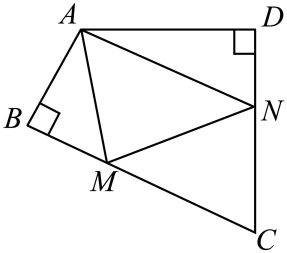 A、130° B、120° C、110° D、100°
A、130° B、120° C、110° D、100°二、填空题(每空5分,共25分)
-
11. 等腰三角形一腰上的高与另一腰的夹角是40°,则该等腰三角形顶角为°.12. 如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是°.
 13. 如图所示,平分于点E, , 那么的长度为.
13. 如图所示,平分于点E, , 那么的长度为. 14. 如图,在中,为边的中线,E为上一点,连接并延长交于点F,若 , , , 则的长为.
14. 如图,在中,为边的中线,E为上一点,连接并延长交于点F,若 , , , 则的长为. 15. 如图,在平面直角坐标系中,直线交轴于点 , 交轴于点 , 且在直线上,点在轴的正半轴上, , 依次均为等腰直角三角形,直角顶点都在轴上,则点的横坐标为 .
15. 如图,在平面直角坐标系中,直线交轴于点 , 交轴于点 , 且在直线上,点在轴的正半轴上, , 依次均为等腰直角三角形,直角顶点都在轴上,则点的横坐标为 .
三、综合题(共8题,共85分)
-
16. 如图,中, .
 (1)、尺规作图:(要求保留作图痕迹,不写作法)
(1)、尺规作图:(要求保留作图痕迹,不写作法)①在上确定一点D,使D到、的距离相等;
②过点D作 , 交于点E;
(2)、在(1)的条件下,则的周长为 .17. “万里桥西一草堂,百花潭水即沧浪”,杜甫草堂的工作人员打算在A、B两点间建立一座观景桥,由于A、B中间隔着河流无法直接测量,数学兴趣小组想在不用涉水的情况下测量此段河流的宽度(该段河流两岸是平的),他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A为参照点;
②沿河岸直走有一棵树C,继续前行到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得的长为 .
(1)、河流的宽度为;(2)、请你证明他们做法的正确性.18. 如图,已知的顶点分别为 , , .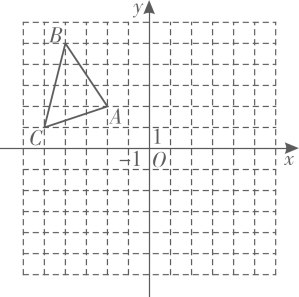 (1)、作出关于x轴对称的图形 .(2)、点P在x轴上运动,当的值最小时,求出点P的坐标.(3)、求的面积.19. 如图,和中,点D在上, , , , 交的延长线于点F.
(1)、作出关于x轴对称的图形 .(2)、点P在x轴上运动,当的值最小时,求出点P的坐标.(3)、求的面积.19. 如图,和中,点D在上, , , , 交的延长线于点F. (1)、求证:;(2)、请直接写出、和之间的数量关系;(3)、求证: .20. 如图,在中, , , 点D在边上,以点A为中心,将线段顺时针旋转得到线段 , 连接 .
(1)、求证:;(2)、请直接写出、和之间的数量关系;(3)、求证: .20. 如图,在中, , , 点D在边上,以点A为中心,将线段顺时针旋转得到线段 , 连接 . (1)、求证:平分;(2)、连接交于点F,过点C
(1)、求证:平分;(2)、连接交于点F,过点C作 , 交的延长线于点G.补全图形,用等式表示线段与之间的数量关系,并证明.
21. 如图,是的角平分线, , 垂足为F,与交于点D.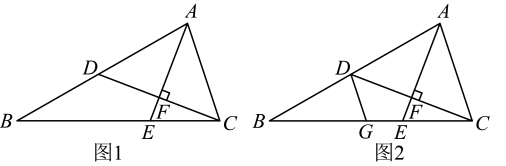 (1)、如图1,若 , , 求的度数;(2)、如图2,点G在线段上,满足 , 求证:与互余.22. 如图,已知:点分别在的边上,连接与交于点 , .
(1)、如图1,若 , , 求的度数;(2)、如图2,点G在线段上,满足 , 求证:与互余.22. 如图,已知:点分别在的边上,连接与交于点 , . (1)、如图1,当都是的角平分线时,求的度数;(2)、如图2,当都是的高时,求的度数;(3)、如图3,当时,探究与的数量关系,并说明理由.23. 在直角三角形ABC中, , 直线l过点C.(1)、当时,
(1)、如图1,当都是的角平分线时,求的度数;(2)、如图2,当都是的高时,求的度数;(3)、如图3,当时,探究与的数量关系,并说明理由.23. 在直角三角形ABC中, , 直线l过点C.(1)、当时,①如图1,分别过点A和B作直线l于点D,直线l于点E.求证:;

②如图2,过点A作直线l于点D,点B与点F关于直线l对称,连接BF交直线l于E,连接CF.求证: .
 (2)、当 , 时,如图3,点B与点F关于直线l对称,连接BF、CF.点M从A点出发,以每秒1cm的速度沿路径运动,终点为C,点N以每秒3cm的速度沿路径运动,终点为F,分别过点M、N作直线l于点D,直线l于点E,点M、N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒.当与全等时,求t的值.
(2)、当 , 时,如图3,点B与点F关于直线l对称,连接BF、CF.点M从A点出发,以每秒1cm的速度沿路径运动,终点为C,点N以每秒3cm的速度沿路径运动,终点为F,分别过点M、N作直线l于点D,直线l于点E,点M、N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒.当与全等时,求t的值.