江苏省盐城地区2023-2024学年苏科版九年级上册数学开学考试试卷

试卷更新日期：2023-08-31 类型：开学考试

进入出卷网下载

一、选择题(每小题3分共24分

1. 如果 $\sqrt{x - 1}$ 在实数范围内有意义，那么x的取值范围是（）

A、 $x > 1$ B、 $x ≥ 1$ C、 $x \leq 1$ D、 $x < 1$

查看试题解析
2. 为了解某校5000名学生的体重情况，随机抽取了200名学生的体重进行统计分析．在该问题中，下列说法正确的是（）

A、这200名学生是总体的一个样本 B、每个学生是个体 C、这5000名学生体重的全体是总体 D、样本容量是200名学生

查看试题解析
3. 下列事件为随机事件的是（）

A、太阳从东方升起 B、你将长到 $5 m$ 高 C、正常情况下，气温低于0 $° C$ 时水结冰 D、抛掷一个均匀的硬币，正面朝上

查看试题解析
4. 如果把 $\frac{3 y}{x + y}$ 中的 $x$ 与 $y$ 都扩大3倍，那么这个代数式的值（）

A、缩小到原来的 $\frac{1}{3}$ B、不变 C、扩大3倍 D、扩大9倍

查看试题解析
5. 若点（ $x_{1}$ ， $y_{1}$ ），（ $x_{2}$ ， $y_{2}$ ），（ $x_{3}$ ， $y_{3}$ ），都是反比例函数 $y = - \frac{1}{x}$ 图像上的点，并且 $y_{1} < 0 < y_{2} < y_{3}$ ，则下列各式中正确的是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{1} < x_{3} < x_{2}$ C、 $x_{2} < x_{1} < x_{3}$ D、 $x_{2} < x_{3} < x_{1}$

查看试题解析
6. 关于x的一元二次方程x²+ax﹣1=0的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
7. 某超市一月份的营业额为100万元，已知第一季度的总营业额共1000万元，如果平均每月增长率为x，则由题意列方程应为（）

A、100（1+x）²=1000 B、100+100×2x=1000 C、100+100×3x=1000 D、100[1+（1+x）+（1+x）²]=1000

查看试题解析
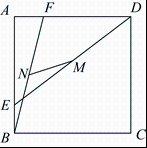8. 如图，正方形 $A B C D$ 边长为6， $A F = B E = 2$ ， M、N分别是 $E D$ 和 $B F$ 的中点，则 $M N$ 长为（）

A、 $\sqrt{5}$ B、 $2 \sqrt{3}$ C、 $\frac{5}{2}$ D、 $\frac{5 \sqrt{2}}{2}$

查看试题解析

二、题空题(每小题3分共30分

9. 若式子 $\frac{x}{x + 1}$ 在实数范围内有意义，则 $x$ 的取值范围是．

查看试题解析
10. 袋子里有5只红球，3只白球，每只球除颜色以外都相同，从中任意摸出1只球，是红球的可能性（选填“大于”“小于”或“等于”）是白球的可能性．

查看试题解析
11. 为确保产品质量，某厂质检部门定期对该厂生产的各类产品按一定比例进行随机检查．并统计产品的合格情况，下图表示的是A产品的部分质检数据：

估计该厂生产的A产品合格的概率是．（结果精确到 $0.01$ ）

查看试题解析
12. 关于 $x$ 的一元二次方程 $x^{2} + 2 x - a = 0$ 的一个根是 $2$ ，则另一个根是．

查看试题解析
13. 如图，将△ABC绕着点 $A$ 顺时针旋转 $x °$ 到△ADE的位置，使点 $E$ 首次落在 $B C$ 上.已知 $∠ A B C = 30 °$ ， $∠ B A E = 35 °$ ，则 $x =$ ．

查看试题解析
14. 如图，在矩形 $O A B C$ 中，点B的坐标为 $(5 ， 12)$ ，则 $A C$ 的长是．

查看试题解析
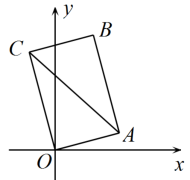15. 关于x的一元二次方程ax²+bx+c＝0满足a﹣b+c＝0，则方程一定有一个根是x＝．

查看试题解析
16. 某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强 $p (P a)$ 是气球体积 $V (m^{3})$ 的反比例函数，且当 $V = 3 m^{3}$ 时， $p = 8000 P a$ ．当气球内的气体压强大于 $40000 P a$ 时，气球将爆炸，为确保气球不爆炸，气球的体积应不小于 $m^{3}$ ．

查看试题解析
17. 在平面直角坐标系 $x O y$ 中，已知 $A (8 ， a)$ ， $B (3 ， b)$ ，以线段 $A B$ 为对角线，作正方形 $A O B C$ ，则点 $C$ 的坐标为．

查看试题解析
18. 如图，将一副三角尺中，含30°角的三角尺（ $△ A B C$ ）的长直角边与含45°角的三角尺（△ACD）的斜边重合，P，Q分别是边AC，BC上的两点，AB与CD交于E，且四边形EPQB是面积为3的平行四边形，则线段DE的长为.

查看试题解析

三、解答题（96分）

19. 计算：

(1)、 $\sqrt{24} - \sqrt{\frac{1}{6}} - \sqrt{6}$ ；

(2)、 $(\sqrt{48} + \frac{1}{4} \sqrt{6}) \div \sqrt{27}$ ．

查看试题解析
20. 先化简，再求值： $(\frac{a^{2} - 1}{a^{2} - 2 a + 1} - \frac{1}{1 - a}) \div \frac{1}{a^{2} - a}$ ，其中 $a$ 满足 $a^{2} + 2 a - 1 = 0$ ．

查看试题解析
21. 解方程：

(1)、(x＋4)²＝5(x＋4)；

(2)、(x－3)(x－1)＝3.

(3)、 $\frac{2 x}{x - 2} = 1 + \frac{1}{x - 2}$ ．

(4)、 $\frac{2 x + 9}{3 x - 9} = \frac{4 x - 7}{x - 3} + 2$ ．

查看试题解析

22. 某机构为了解宿迁市人口年龄结构情况，对宿迁市的人口数据进行随机抽样分析，绘制了尚不完整的统计图表：

人口年龄结构统计表

类别	A	B	C	D
年龄（t岁）	0≤t＜15	15≤t＜60	60≤t＜65	t≥65
人数（万人）	4.7	11.6	m	2.7

根据以上信息解答下列问题：

(1)、本次抽样调查，共调查了万人；

(2)、请计算统计表中m的值以及扇形统计图中“C”对应的圆心角度数；

(3)、宿迁市现有人口约500万人，请根据此次抽查结果，试估计宿迁市现有60岁及以上的人口数量．

查看试题解析

23. 刘阿姨到超市购买大米，第一次按原价购买，用了 $105$ 元.几天后，遇上这种大米 $8$ 折出售，她用 $140$ 元又买了一些，两次一共购买了 $40$ kg.这种大米的原价是多少？

查看试题解析
24. 如图，在矩形 $A B C D$ 中， $B E ⊥ A C$ ， $D F ⊥ A C$ ，垂足分别为E、F ．求证： $A F = C E$ ．

查看试题解析
25. 如图，在 $▱ A B C D$ 中， $A B = 5$ ， $A D = 3 \sqrt{2}$ ， $∠ A = 45 °$ ．

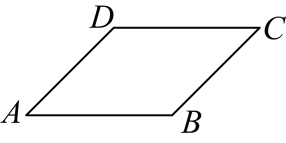(1)、求出对角线 $B D$ 的长；

(2)、尺规作图：将四边形 $A B C D$ 沿着经过 $A$ 点的某条直线翻折，使点 $B$ 落在 $C D$ 边上的点 $E$ 处，请作出折痕．（不写作法，保留作图痕迹）

查看试题解析
26. 如图， $△ A B C$ 中，点D是 $A B$ 上一点，点E是 $A C$ 的中点，过点C作 $C F ∥ A B$ ，交 $D E$ 的延长线于点F ．

(1)、求证： $△ A D E ≌ △ C F E$ ；

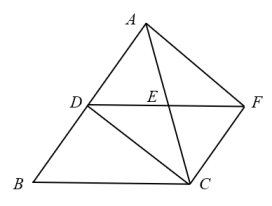(2)、连接 $A F ， C D$ ，如果点D是 $A B$ 的中点，那么当 $A C$ 与 $B C$ 满足什么条件时，四边形 $A D C F$ 是菱形？证明你的结论．

查看试题解析
27. “数形结合”是一种重要的数学思想，八上教材中，我们曾用函数观点看方程，也就是利用一次函数的图象求解二元一次方程组．类似的，学习了一次函数和反比例函数之后，我们也可以将方程的解的研究转化为已学函数图象交点的问题……

(1)、方程 $x^{2} - 2 x - 3 = 0$ 的解可以转化为一次函数 $y_{1}$ 和反比例函数 $y_{2}$ 的图像交点问题．请直接写出一对符合要求的 $y_{1}$ 和 $y_{2}$ 的表达式；

(2)、利用“数形结合”，不解方程，借助下面平面直角坐标系，判断方程 $x | x - 2 | = 4$ 的解的个数．

查看试题解析
28. 如图，在平面直角坐标系 $x O y$ 中，点A的坐标为 $(4 \sqrt{3} ， 0)$ ，已知点 $M (5 ， 3 \sqrt{3})$ 、点C在反比例函数 $y = \frac{k}{x} (x > 0)$ 图象上．

(1)、 $k =$ ；

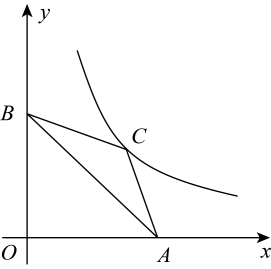(2)、若点A关于点C的对称点D也在反比例函数图象上，求此时点C的坐标；

(3)、若点A绕点C顺时针旋转 $120 °$ ，所得对应点B刚好落在y轴的正半轴上，求线段 $A B$ 的长．

查看试题解析