沪科版数学八年级上册第14章全等三角形章末过关检测卷

试卷更新日期：2023-08-31 类型：单元试卷

进入出卷网下载

一、选择题（每题4分，共40分）

1. 下列各组中的两个图形属于全等图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列命题属于假命题的是（）

A、三个角对应相等的两个三角形全等 B、三边对应相等的两个三角形全等 C、全等三角形的对应边相等 D、全等三角形的面积相等

查看试题解析
3. 已知图中的两个三角形全等，则∠α的度数是（）

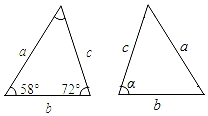A、72° B、60° C、58° D、50°

查看试题解析
4. 如图，△ABC≌△ADE，若∠BAE=120，∠BAD=40°，则∠BAC的度数为（）

A、40° B、80° C、120° D、100°

查看试题解析
5. 安装空调一般会采用如图的方法固定，其根据的几何原理是（）

A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短

查看试题解析
6. 如图，已知 $∠ A B C = ∠ D E C ， B E = C F$ ，添加下列条件不能判定 $△ A B C ≌ △ D E F$ 的是（）

A、 $A C = D F$ B、 $∠ A C B = ∠ D F E$ C、 $∠ A = ∠ D$ D、 $A B = D E$

查看试题解析
7. 下面各图中所给数据的三角形，则甲、乙、丙三个三角形和左侧 $△ A B C$ 全等的是（）

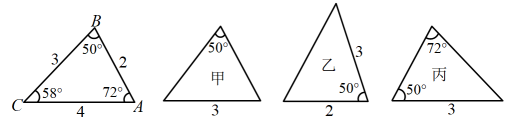A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙

查看试题解析
8. 在测量一个小口圆形容器的壁厚时，小明用“ $X$ 型转动钳”按如图方法进行测量，其中OA＝OD，OB＝OC，测得AB＝5厘米，EF＝7厘米，圆形容器的壁厚是（　　）

A、1厘米 B、2厘米 C、5厘米 D、7厘米

查看试题解析
9. 如图， $A D$ 是 $△ A B C$ 的中线，E，F分别是 $A D$ 和 $A D$ 延长线上的点，且 $D E = D F$ ，连接 $B F$ ， $C E$ ，下列说法：① $△ A B D$ 和 $△ A C D$ 面积相等；② $∠ B A D = ∠ C A D$ ；③ $△ B D F ≅ △ C D E$ ；④ $B F ∥ C E$ ；⑤ $C E = A E$ ．其中正确的是（　　）

A、①② B、③⑤ C、①③④ D、①④⑤

查看试题解析
10. 如图，已知在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，直角 $∠ E P F$ 的顶点P是 $B C$ 的中点，两边 $P E$ 、 $P F$ 分别交 $A B$ 、 $A C$ 于点E、F.以下四个结论：① $A E = C F$ ；② $△ E P F$ 是等腰直角三角形；③ $S_{四边形 A E P F} = \frac{1}{2} S_{△ A B C}$ ；④ $E F = A P$ .其中正确的是（）

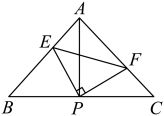A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

二、填空题（每空5分，共20分）

11. 如图所示，一块三角形玻璃碎成了4块，现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃，那么最省事的办法是带．

查看试题解析
12. 如图，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度 $A C$ 与右边滑梯的水平长度 $D F$ 相等，那么判定 $△ A B C$ 与 $△ D E F$ 全等的依据是．

查看试题解析
13. 如图，已知方格纸中是4个相同的正方形，则 $∠ 1 + ∠ 2 + ∠ 3 =$ 度.

查看试题解析
14. 如图，AB=4cm，AC=BD=3cm．∠CAB=∠DBA=60°，点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．设点Q的运动速度为xcm/s，若使得△ACP与△BPQ全等．x的值为．

查看试题解析

三、解答题（共2题，共8分）

15. 如图，已知 $△ A B C ≌ △ D B E$ ，点D在 $A C$ 上， $B C$ 与 $D E$ 交于点P．若 $∠ A B E = 160 °$ ， $∠ D B C = 30 °$ ，求 $∠ C B E$ 的度数．

查看试题解析
16. 如图，在 $△ A B C$ 中，已知 $A D$ 是 $B C$ 边上的中线， $E$ 是 $A D$ 上一点，且 $B E = A C$ ，延长 $B E$ 交 $A C$ 于点 $F$ ，求证： $A F = E F$ ．

查看试题解析

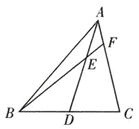
四、综合题（共8题，共82分）

17. 小明回顾了一下用尺规作一个角等于已知角的过程：

已知： $∠ A O B$ ．求作： $∠ A^{'} O^{'} B^{'} = ∠ A O B$ ．

作法如下：①作射线 $O^{'} B^{'}$ ；

②以点O为圆心，任意长为半径作弧，分别交 $O A$ 于点D，交 $O B$ 于点E；

③以点 $O^{'}$ 为圆心， $O D$ 长为半径作弧，交 $O^{'} B^{'}$ 于点 $E^{'}$ ；

④以点 $E^{'}$ 为圆心， $D E$ 长为半径作弧，交前弧于点D'；

⑤过点 $D^{'}$ 作射线 $O^{'} A^{'}$ ． $∠ A^{'} O^{'} B^{'}$ 就是所求作的角．

请你根据以上材料完成下列问题：

(1)、完成下面说理过程(将正确答案填在相应的横线上)；

如图，分别连接 $D E$ ， $D^{'} E^{'}$ ；

由作图可知， $O D = O^{^{'}} D^{^{'}}$ ， $O E =$ ▲ ， $D E =$ ▲ ，

所以 $△ D O E ≌$ ▲ ， ( $S S S$ )

所以 $∠ A O B = ∠ A^{^{'}} O^{^{'}} B^{^{'}}$ ． (依据)

(2)、上面说理过程中的依据是：．

查看试题解析

18. 如图，在 $△ A B C$ 中， $∠ B = ∠ C$ ， E，F为BC边上的两点，且F在E的右侧.已知 $B E = C F$ .

(1)、求证： $A E = A F$ ；

(2)、若点D在AF的延长线上， $A D = A C$ ， $∠ B A E = 30 °$ ， $∠ B A D = 75 °$ ，求证： $A B ∥ D C$ .

查看试题解析
19. 在 $△ A B C$ 中， $A B = C B$ ， $∠ A B C = 90 °$ ， F为 $A B$ 延长线上一点，点E在 $B C$ 上，且 $A E = C F$ ．

(1)、求证： $R t △ A B E ≌ R t △ C B F$ ；

(2)、若 $∠ C A E = 32 °$ ，求 $∠ A C F$ 度数．

查看试题解析
20. 如图，点 $D$ 是等边 $△ A B C$ 外一点， $∠ B D C = 120 °$ ， $D B = D C$ ，点 $E$ ， $F$ 分别在 $A B$ ， $A C$ 上，连接 $A D$ 、 $D E$ 、 $D F$ 、 $E F$ .

(1)、求证： $A D$ 是 $B C$ 的垂直平分线；

(2)、若 $E D$ 平分 $∠ B E F$ ， $B C = 5$ ，求 $△ A E F$ 的周长.

查看试题解析
21. 如图①， $A B = A C$ ， $A D = A E$ ， $∠ B A C = ∠ D A E$ ，连接BD，CE．

(1)、 $△ A B D$ 与 $△ A C E$ 全等吗？请说明理由；

(2)、如图②，延长CE交线段AB于点G，交线段BD于点F，若 $∠ C = 30 °$ ， $∠ E A G = 60 °$ ，且点E在线段AC的垂直平分线上，求 $∠ B F C$ 的度数．

查看试题解析
22. 已知，在等边三角形 $A B C$ 中，点O在 $A B$ 上，点P在 $C B$ 的延长线上，且 $O P = O C$ .

(1)、如图1，当点O为 $A B$ 的中点时，确定线段 $A O$ 与 $P B$ 的大小关系，请你直接写出结论；

(2)、如图2，当点O为 $A B$ 边上任意一点，确定线段 $A O$ 与 $P B$ 的大小关系，请你写出结论，并说明理由；

(3)、在等边三角形 $A B C$ 中，点O在直线 $A B$ 上，点P在线段 $C B$ 的延长线上，且 $O P = O C$ ，若 $△ A B C$ 的边长为2， $A O = 5$ ，求 $C P$ 的长.（请画出相应图形，并写出解题过程）

查看试题解析
23. 在 $△ A B C$ 中， $∠ A C B ＝ 9 0^{o} ， A C ＝ B C$ ，直线 $M N$ 经过点C，且 $A D ⊥ M N$ 于D， $B E ⊥ M N$ 于E．

(1)、当直线 $M N$ 绕点C旋转到图1的位置时，求证：
① $△ A C D ≌ △ C E B$ ；
② $D E ＝ A D ＋ B E$ ．

(2)、当直线 $M N$ 绕点C旋转到图2的位置时，求证： $D E ＝ A D - B E$ ；

(3)、当直线 $M N$ 绕点C旋转到图3的位置时，试问 $D E 、 A D 、 B E$ 具有怎样的等量关系？请写出这个等量关系，并加以证明．

查看试题解析
24. 在四边形ABCD中.

(1)、如图1，AB＝AD，∠ABC＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝ $\frac{1}{2}$ ∠DAB，探究图中EF，BE，DF之间的数量关系.
小林同学探究此问题的方法是：延长CB到点G，使BG＝DF.连接AG，先对比△ABG与△ADF的关系，再对比△AEF与△AEG的关系，可得出EF、BE、DF之间的数量关系，他的结论是；

(2)、如图2，在四边形ABCD中，AB＝AD，∠B+∠ADF＝180°，E、F分别是BC，CD上的点，且∠EAF＝ $\frac{1}{2}$ ∠DAB，则上述结论是否仍然成立，请说明理由.

(3)、如图3，在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝AD，若点F在CB的延长线上，点E在CD的延长线上，若EF＝BF+DE，请写出∠EAF与∠DAB的数量关系，并给出证明过程.

查看试题解析